Login/Sign Up
Home » A irregular plank weighing is suspended in the manner shown below, by strings of negligible weight. If the strings make an angle of and respectively with the vertical, find the location of center of gravity of the plank from the left end.
A 2 \mathrm{~m} irregular plank weighing \mathrm{W} \mathrm{kg} is suspended in the manner shown below, by strings of negligible weight. If the strings make an angle of 35^{0} and 55^{\circ} respectively with the vertical, find the location of center of gravity of the plank from the left end.
CBSE | Class 11 | NCERT | Physics | System of Particles and Rotational Motion
A 2 \mathrm{~m} irregular plank weighing \mathrm{W} \mathrm{kg} is suspended in the manner shown below, by strings of negligible weight. If the strings make an angle of 35^{0} and 55^{\circ} respectively with the vertical, find the location of center of gravity of the plank from the left end.

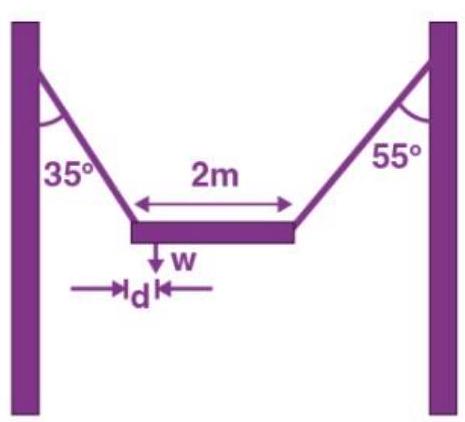
Following is the FBD(Free Body Diagram) for the above figure:

Length of the plank is given as \mid=2 \mathrm{~m}

\theta_{1}=35^{\circ} and \theta_{2}=55^{\circ}

Let the tensions produced in the left and right strings respectively be T_{1} and T_{2}.

So at translational equilibrium we can have,

\mathrm{T}_{1} \sin \theta_{1}=\mathrm{T}_{2} \sin \theta_{2}

\mathrm{T}_{1} / \mathrm{T}_{2}=\sin \theta_{2} / \sin \theta_{1}=\sin 55 / \sin 35

\mathrm{T}_{1} / \mathrm{T}_{2}=0.819 / 0.573=1.42

\mathrm{T}_{1}=1.42 \mathrm{~T}_{2}

Let the distance of the center of gravity of the plank from the left be ‘ d ‘.

For rotational equilibrium about the centre of gravity, we can write,

T_{1} \cos 35 \times d=T_{2} \cos 55(2-d)

\left(\mathrm{T}_{1} / \mathrm{T}_{2}\right) \times 0.82 \mathrm{~d}=(2 \times 0.57-0.57 \mathrm{~d})

Putting \mathrm{T}_{1}=1.42 \mathrm{~T}_{2}

1.42 \times 0.82 \mathrm{~d}+0.57 \mathrm{~d}=1.14

1.73 \mathrm{~d}=1.14

As a result, d=0.65 \mathrm{~m}

i

More Material