Solution:
Let ![]() be the event of bag selection. The event of choosing the bag, say bag II, and the event of drawing a red ball are represented by
be the event of bag selection. The event of choosing the bag, say bag II, and the event of drawing a red ball are represented by ![]() and
and ![]() , respectively.
, respectively.
Then ![]()
Also ![]() (drawing a red ball from bag I) =
(drawing a red ball from bag I) = ![]()
And ![]() (drawing a red ball from bag II) =
(drawing a red ball from bag II) = ![]()
Given that the ball in bag 1 is red, the probability of drawing it is ![]() .
.
By using Bayes’ theorem, we have:

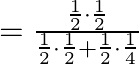
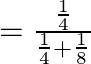
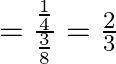
![]()
