For a binary operation if a*e = a, then e s called the right identity
If ![]() then
then ![]() is called the left identity
is called the left identity
For the given binary operation,
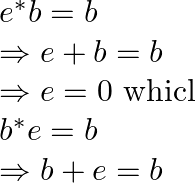
![]() which is less than 6
which is less than 6
![]()
![]()
![]() which is less than 6
which is less than 6
For the ![]() condition,
condition,
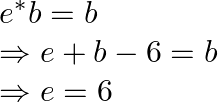
But ![]() does not belong to the given set
does not belong to the given set ![]()
So the identity element is 0
An element ![]() is said to be the inverse of a, if
is said to be the inverse of a, if ![]() e where e is the identity element
e where e is the identity element
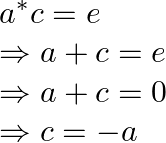
a belongs to ![]() ,
,
– a belongs to ![]()
So c belongs to ![]() ,
,
So ![]() is not the inverse for all elements
is not the inverse for all elements ![]()
Putting in the ![]() condition
condition
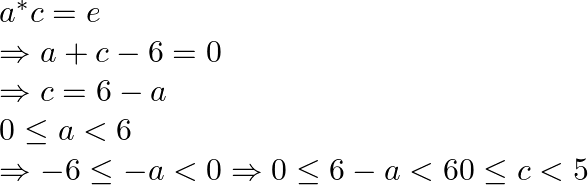
=> ![]() belongs to the given set
belongs to the given set
Hence the inverse of the element a is (6-a)

![Rendered by QuickLaTeX.com \[a * b=\left\{\begin{array}{ll} a+b ; & \text { if } a+b<6 \\ a+b-6 ; & \text { if } a+b \geq 6 \end{array}\right.\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c98db70d6373f329a8c6803f36eeb4ad_l3.png)