Login/Sign Up
Home » A die is thrown three times, E: 4 appears on the third toss, and 5 appears respectively on first two tosses.
A die is thrown three times, E: 4 appears on the third toss, \mathrm{F}: 6 and 5 appears respectively on first two tosses.
CBSE | Maths | NCERT | Probability
A die is thrown three times, E: 4 appears on the third toss, \mathrm{F}: 6 and 5 appears respectively on first two tosses.

Solution:

In the sample space, there are 216 outcomes, with each element of the sample space having three entries and taking the form

(x, y, z) where 1 \leq x, y, z \leq 6.

Considering the event, E: 4 appears on the third toss

    \[\Rightarrow \mathrm{E}=\left{\begin{array}{l}(1,1,4),(1,2,4),(1,3,4),(1,4,4),(1,5,4),(1,6,4), \(2,1,4),(2,2,4),(2,3,4),(2,4,4),(2,5,4),(2,6,4), \(3,1,4),(3,2,4),(3,3,4),(3,4,4),(3,5,4),(3,6,4), \(4,1,4),(4,2,4),(4,3,4),(4,4,4),(4,5,4),(4,6,4), \(5,1,4),(5,2,4),(5,3,4),(5,4,4),(5,5,4),(5,6,4), \(6,1,4),(6,2,4),(6,3,4),(6,4,4),(6,5,4),(6,6,4)\end{array}\right}\]

Now the event, F: 6 and 5 appears respectively on first two tosses

    \[\Rightarrow F={(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6)}\]

\Rightarrow E \cap F={(6,5,4)}

So, P(E)=\frac{36}{216}, P(F)=\frac{6}{216}, P(E \cap F)=\frac{1}{216}

Now, we know that by definition of conditional probability, 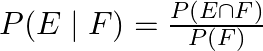P(E \mid F)=\frac{P(E \cap F)}{P(F)}

Now by substituting the values we get

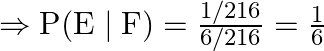
\Rightarrow \mathrm{P}(\mathrm{E} \mid \mathrm{F})=\frac{1 / 216}{6 / 216}=\frac{1}{6}

\Rightarrow \mathrm{P}(\mathrm{E} \mid \mathrm{F})=\frac{1}{6}

i

More Material