Login/Sign Up
Home » As shown in Figure the two sides of a step ladder BA and CA are long and hinged at A. A rope DE, m is tied halfway up. A weight is suspended from a point F, from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take ) (Hint: Consider the equilibrium of each side of the ladder separately.)
As shown in Figure the two sides of a step ladder BA and CA are 1.6 \mathbf{m} long and hinged at A. A rope DE, 0.5 m is tied halfway up. A weight 40 \mathrm{~kg} is suspended from a point F, 1.2 \mathrm{~m} from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8 \mathrm{m} / \mathbf{s}^{2} ) (Hint: Consider the equilibrium of each side of the ladder separately.)
CBSE | Class 11 | NCERT | Physics | System of Particles and Rotational Motion
As shown in Figure the two sides of a step ladder BA and CA are 1.6 \mathbf{m} long and hinged at A. A rope DE, 0.5 m is tied halfway up. A weight 40 \mathrm{~kg} is suspended from a point F, 1.2 \mathrm{~m} from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8 \mathrm{m} / \mathbf{s}^{2} ) (Hint: Consider the equilibrium of each side of the ladder separately.)

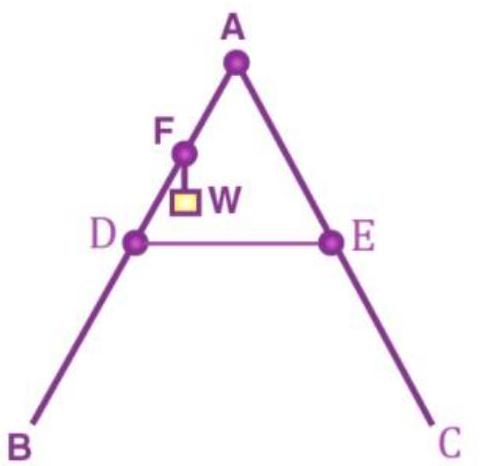
Solution:

The above figure can be redrawn as,

where,

N_{B} is the force being applied by floor point B on the ladder

N_{c} is the force being applied by floor point C on the ladder

The tension in the ring be T

B A=C A=1.6 \mathrm{~m}

\mathrm{DE}=0.5 \mathrm{~m}

\mathrm{BF}=1.2 \mathrm{~m}

Mass of the weight is given as m=40 \mathrm{~kg}

Now,

We will construct a perpendicular from A on the floor B C. This will intersect DE at mid-point H.

\triangle \mathrm{ABl} and \triangle \mathrm{AlC} are similar

\therefore \mathrm{B} \mid=\mathrm{IC}

This makes I the mid-point of B C.

\mathrm{DE} \| \mathrm{BC}

B C=2 \times D E=1 \mathrm{~m} A F

B A-B F=1.6-1.2=0.4 m \ldots \ldots \ldots(1)

D is the mid-point of A B.

Thus,

A D=(1 / 2) \times B A=0.8 m \quad \ldots \ldots \ldots \ldots(2)

On using equations (1) and (2), we get:

D F=0.4 \mathrm{~m}

As a result, F is the mid-point of A D.

FG || DH and we concluded that F is the mid-point of AD. This will make G the mid-point of AH.
ΔAFG and ΔADH are similar
∴ FG / DH = AF / AD
FG / DH =  0.4 / 0.8  =  1 / 2
FG = (1/2) DH

Since, H is the midpoint of the rope, so DH = 0.5/2 = 0.25 m
= (1/2) × 0.25  =  0.125 m

In ΔADH:
AH = (AD2 – DH2)1/2
= (0.82 – 0.252)1/2  =  0.76 m

The downward force should be equal to the upward force for translational equilibrium of the ladder, so,
NC+ NB = mg = 392 N . . .. . . . . . . . . . . . . .  ( 3 )      [ mg = 9.8 x 40 ]
Rotational equilibrium of the ladder about A is can be calculated as,
-NB × BI +  FG x mg + NC × CI – T × AG + AG × T =  0
-NB× 0.5 + 392× 0.125 + NC × 0.5  =  0
(NC – NB) × 0.5 = 49
NC – NB = 98       . . . . . . . . . .. . . .. . .. . . ( 4 )
On aAdding equations (3) and (4), we get:
NC = 245 N
NY = 147 N
Rotational equilibrium about AB

Considering the moment about A
-NB × BI +  FG x mg + T × AG  =  0
-245× 0.5 + 392 × 0.125 + 0.76 x T  =  0
∴ T = 96.7 N.

i

More Material