(i) LHS:
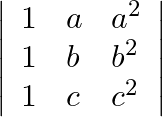
![]() and
and ![]()
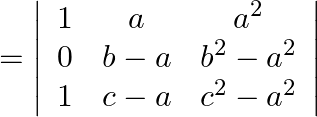
Expanding ![]() column,
column,
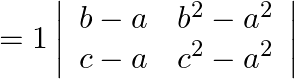
Taking (b-a) common from first row,
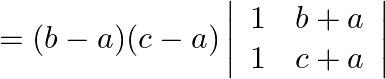
Simplifying above expression, we have
![]()
![]()
![]()
Proved.
(ii) ![]()
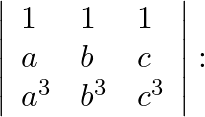
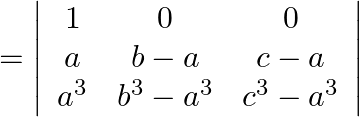
Expanding first row
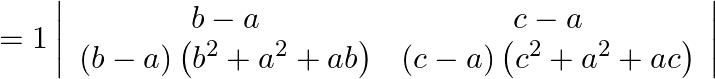
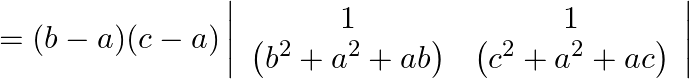
![]()
![]()
Proved
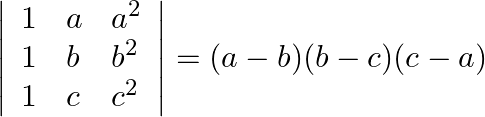 (ii)
(ii) 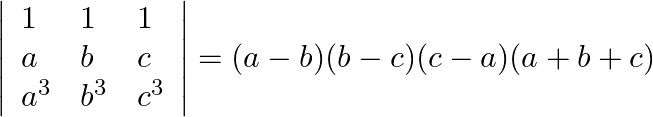
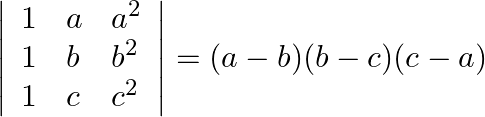 (ii)
(ii) 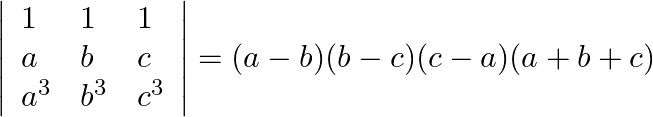
(i) LHS:
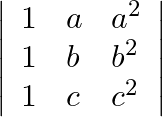
![]() and
and ![]()
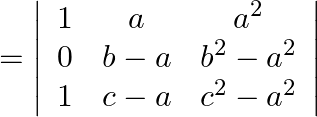
Expanding ![]() column,
column,
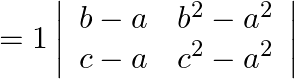
Taking (b-a) common from first row,
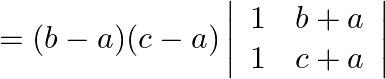
Simplifying above expression, we have
![]()
![]()
![]()
Proved.
(ii) ![]()
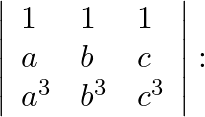
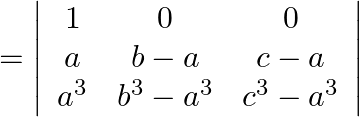
Expanding first row
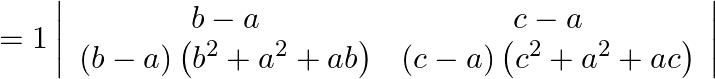
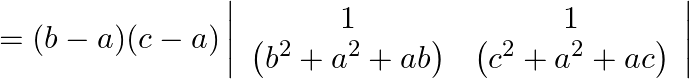
![]()
![]()
Proved