Login/Sign Up
Home » Calculate the mean deviation about the mean of the set of first natural numbers when is an even number.
Calculate the mean deviation about the mean of the set of first n natural numbers when \mathrm{n} is an even number.
CBSE | Class 11 | Maths | NCERT Exemplar | Statistics
Calculate the mean deviation about the mean of the set of first n natural numbers when \mathrm{n} is an even number.

Solution:

It is given that set of first n natural numbers when \mathrm{n} is an even number.

We now need to find the mean deviation about the mean

It is known that the first n natural numbers are 1,2,3 \ldots . \ldots \mathrm{n}. And given n is even number.

Therefore the mean is,

\overline{\mathrm{x}}=\frac{1+2+3+\cdots+\mathrm{n}}{\mathrm{n}}=\frac{\frac{\mathrm{n}(\mathrm{n}+1)}{2}}{\mathrm{n}}=\frac{(\mathrm{n}+1)}{2}

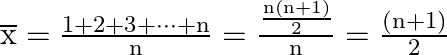
Deviations of numbers from the mean are as shown below,

1-\frac{(n+1)}{2}, 2-\frac{(n+1)}{2}, 3-\frac{(n+1)}{2}, \ldots, \frac{(n-2)}{2}-\frac{(n+1)}{2}, \frac{(n)}{2} -\frac{(n+1)}{2}, \frac{(n+2)}{2}-\frac{(n+1)}{2}, \ldots, n-\frac{(n+1)}{2}

Or, \frac{2-(n+1)}{2}, \frac{4-(n+1)}{2}, \frac{6-(n+1)}{2}, \ldots, \frac{n-2-(n+1)}{2}, \frac{n-(n+1)}{2}, \frac{(n+2)-(n+1)}{2}, \ldots, \frac{2 n-(n+1)}{2}

Above eq. can be written as \frac{2-(n+1)}{2}, \frac{4-(n+1)}{2}, \frac{6-(n+1)}{2}, \ldots \ldots, \frac{-3}{2}, \frac{-1}{2}, \frac{1}{2} \ldots, \frac{2 n-(n+1)}{2}

Or,

\frac{1-\mathrm{n}}{2}, \frac{3-\mathrm{n}}{2}, \frac{5-\mathrm{n}}{2}, \ldots \ldots, \frac{-3}{2}, \frac{-1}{2}, \frac{1}{2}, \ldots, \frac{\mathrm{n}-1}{2}

Therefore, the absolute values of deviation from the mean is

\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|=\frac{(\mathrm{n}-1)}{2}, \frac{(\mathrm{n}-3)}{2}, \frac{(\mathrm{n}-5)}{2}, \ldots \ldots, \frac{3}{2}, \frac{1}{2}, \frac{1}{2}, \ldots, \frac{\mathrm{n}-1}{2}

Sum of absolute values of deviations from the mean, is \sum\left|x_{i}-\bar{x}\right|=\frac{(n-1)}{2}+\frac{(n-3)}{2}+\frac{(n-5)}{2}+\cdots+\frac{3}{2}+\frac{1}{2}+\frac{1}{2}+\cdots+\frac{n-1}{2}

It can be written as

\sum\left|\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|=\left(\frac{1}{2}+\frac{3}{2}+\cdots+\frac{(\mathrm{n}-1)}{2}\right)\left(\frac{\mathrm{n}}{2}\right)

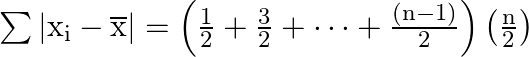
It is known that the sum of first n natural numbers =n^{2}

Hence, the mean deviation about the mean is

M.D 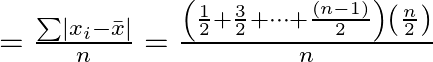=\frac{\sum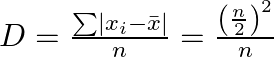\left|x_{i}-\bar{x}\right|}{n}=\frac{\left(\frac{1}{2}+\frac{3}{2}+\cdots+\frac{(n-1)}{2}\right)\left(\frac{n}{2}\right)}{n}

M. D=\frac{\sum\left|x_{i}-\bar{x}\right|}{n}=\frac{\left(\frac{n}{2}\right)^{2}}{n}

M. D=\frac{\sum\left|x_{i}-\bar{x}\right|}{n}=\frac{n^{2}}{4 n}=\frac{n}{4}

As a result, n / 4 is the mean deviation about the mean of the set of first n natural numbers when n is an even number.

i

More Material