Chloride radical is detected by the chromyl chloride test. In this test, chromyl chloride gas (orange red color) is produced. Equation Involved – 4NaCl + K2Cr2O7 + 6H2SO4 → 4NaHSO4 + 2KHSO4 + 3H2O +...
What do you understand by lanthanide contraction
The lanthanide contraction is the decrease in the atomic or ionic radii with increase in the atomic number of lanthanides
What are lanthanide elements?
Lanthanide elements resembles a lot in properties with lanthanum. Lanthanide is group of 14 elements from atomic number 58 to 71. In these elements on increasing atomic number electron enters into...
Explain oxidization properties of potassium permanganate in acidic medium.
2KMnO4 + 8H2SO4 + 10KI → 6K2SO4 + 8H2O + 5I2 2KMnO4 + 5SO2 + 2H2O → 2MnSO4 + 2H2SO4 + K2SO4 2KmO4 + 16HCl → 2KCl + 2MnCl2 + 8H2O + 5Cl2 5COOH – COOH + [5O] → 10CO2 + 5H2O
Give two differences between double salt and complex salt.
Answer: Double salt Complex salt A double salt is a combination of two salt compounds. A complex salt is a molecular structure that is composed of one or more complex ions. Double salts can give...
Give two differences between DNA and RNA.
Answer: DNA RNA DNA – Deoxyribo Nucleic Acid RNA – Ribo Nucleic acid DNA consists of adenine (A), cytosine (C), guanine (G), and thymine (T) RNA consists of adenine (A), cytosine (C), guanine (G),...
Find the shortest distance between the given lines. ![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
Answer Given equations: r¯=(ı^+ȷ^)+λ(2ı^-ȷ^+k^) \overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})...
Which of the following compounds has tetrahedral geometry? (a) ![Rendered by QuickLaTeX.com \left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{-2}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c5a91864ba7e1e0ed1b5d273d822f5e5_l3.png) (b)
(b) ![Rendered by QuickLaTeX.com \left[\mathrm{Pd}(\mathrm{CN})_{4}\right]^{2-}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ffda616d3dbe7dc8925722e87005924e_l3.png) (c)
(c) ![Rendered by QuickLaTeX.com \left[\mathrm{PdCl}_{4}\right]^{2-}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-90cc6a4f4d42dee46e06d6f8ed516b7a_l3.png) (d)
(d) ![Rendered by QuickLaTeX.com \left[\mathrm{NiCl}_{4}\right]^{2}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-149ee5c95bd9cfcc4405704fba2e1bab_l3.png)
SOL: Correct option is D. $\left[\mathrm{NiCl}_{4}\right]^{2}$
Oxidation number of gold metal is (a)+1 (b) 0 (c) 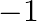 (d) all of these
(d) all of these
Sol: Correct option is B. 0
Question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
(a) Both Assertion (A) and reason (R) are true and Reason (R) is a correct explanation of Assertion (A). (b) Both Assertion (A) and reason (R) are true and Reason (R) is not a correct explanation of...
Question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
(a) Both Assertion (A) and reason (R) are true and Reason (R) is a correct explanation of Assertion (A). (b) Both Assertion (A) and reason (R) are true and Reason (R) is not a correct explanation of...
Match the following:
The mean of 2, 7, 6 and x is 15 and mean of 18, 1, 6, x and y is 10. What is the value of y? (a) 5 (b) 10 (c) -20 (d) 30
If the median of the data 4, 7, x-1, x-3, 16, 25, written in ascending order, is 13 then x is equal to
(a) 13 (b) 14 (c) 15 (d) 16 Answer: (c) 15 Sol: Median of 6 numbers is the average of 3rd and 4th term. ∴ 13 = (????−1)+(????−3) 2 ⇒ 26 = 2x – 4 ⇒ 2x = 30 ⇒ x = 15 Thus, x is equal to...
The mean of 20 numbers is 0. OF them, at the most, how many may be greater than zero?
(a) 0 (b) 1 (c) 10 (d) 19 Answer: (d) 19 Sol: It is given that mean of 20 numbers is zero. i.e., average of 20 numbers is zero. i.e., sum of 20 numbers is zero. Thus, at most, there can be 19...
The median of the first 8 prime numbers is
(a) 7 (b) 9 (c) 11 (d) 13 Answer: (b) 9 Sol: First 8 prime numbers are 2, 3, 5, 7, 11, 13, 17 and 19. Median of 8 numbers is average of 4th and 5th terms.
Look at the cumulative frequency distribution table given below:
Answer: (c) 13 Sol: Converting the given data into a frequency table, we get: Hence, the number of families having an income range of Rs. 20,000 – Rs. 25,000 is 13. The correct option is...
For a symmetrical frequency distribution, we have:
(a) mean ˂ mode ˂ median (b) mean > mode > median (c) mean = mode = median (d) mode = 1 2 (mean + median) Answer: (c) mean = mode = median Sol: A symmetric distribution is one where the left...
The median and mode of a frequency distribution are 26 and 29 respectively. Then, the mean is
(a) 27.5 (b) 24.5 (c) 28.4 (d) 25.8 Answer: (b) 24.5 Sol: Mode = (3 × median) – (2 × mean) ⇒ (2 × mean) = (3 × median) – mode ⇒ (2 × mean) = 3 × 26 – 29 ⇒ (2 × mean) = 49 ⇒ Mean = 49 2 ∴ Mean = 24.5...
The mean and mode of a frequency distribution are 28 and 16 respectively. The median is
(a) 22 (b) 23.5 (c) 24 (d) 24.5 Answer: (c) 24 Sol: Mode = (3 × median) – (2 × mean) ⇒ (3 × median) = (mode + 2 mean) ⇒ (3 × median) = 16 + 56 ⇒ (3 × median) = 72 ⇒ Median = 72 3 ∴...
Consider the following table:
Look at the frequency distribution table given below:
If the mean and median of a set of numbers are 8.9 and 9 respectively, then the mode will be
(a) 7.2 (b) 8.2 (c) 9.2 (d) 10.2 Answer: (c) 9.2 Sol: It is given that the mean and median are 8.9 and 9, respectively, ∴ Mode = (3 × Median) – (2 × Mean) ⇒ Mode = (3 × 9) – (2 × 8.9) = 27 – 17.8 =...
Median =?
Mode = ?
Consider the following frequency distribution
Consider the frequency distribution of the heights of 60 students of a class
if the ‘less than type’ ogive and ‘more than type’ ogive intersect each other at (20.5, 15.5) then the median of the given data is
(a) 5.5 (b) 15.5 (c) 20.5 (d) 36.0 Answer: (c) 20.5 Sol: The x- coordinate represents the median of the given data. Thus, median of the given data is 20.5.
The relation between mean, mode and median is
(a) mode=(3 * mean) – (2 * median) (b) mode=(3 *median) – (2 *mean) (c) median=(3 * mean) – (2 * mode) (d) mean=(3 * median) – (2 *mode) Answer: (b) mode=(3 * median) – (2 *mean) Sol: mode=(3 *...
While computing the mean of the groue data, we assume that the frequencies are
(a) evenly distributed over the classes (b) centred at the class marks of the classes (c) centred at the lower limits of the classes (d) centred at the upper limits of the classes Answer: (b)...
In the formula for the following the mean of the grouped data, the i d ’s are the deviations from A of
(a) lower limits of the classes (b) upper limits of the classes (c) midpoints of the classes (d) none of these Answer: (c) midpoints of the classes Sol: The ???????? ′???? are the deviations from A...
For the finding the mean by using the formula,
If ‘ i x s are the midpoints of the class intervals of a grouped data, ‘ i f s are the corresponding frequencies and x is the mean then
The abscissa of the point of intersection of the Less Than Type and of the More Than Type cumulative frequency curves of a grouped data gives its
(a) Mean (b) Median (c) Mode (d)None of these Answer: (b) Median Sol: The abscissa of the point of intersection of the ‘less than type’ and that of the ‘more than type’ cumulative...
The cumulative frequency table is useful is determining the
(a) Mean (b) Median (c) Mode (d) all of these Answer: (b) Median Sol: The cumulative frequency table is useful in determining the median.
The medium of a frequency distribution is found graphically with the help of
(a) a histogram (b) a frequency curve (c) a frequency polygon (d) ogives Answer: (d) ogives Sol: This because median of a frequency distribution is found graphically...
The mode of frequency distribution is obtained graphically from
(a) a frequency curve (b) a frequency polygon (c) a histogram (d) an ogive Answer: (c) a histogram Sol: The mode of a frequency distribution can be obtained graphically from a histogram.
Which of the following measures of central tendency is influence by extreme values?
(a) Mean (b) Median (c) Mode (d) None of these Answer: (a) Mean Sol: Mean is influenced by extreme values.
Which of the following cannot be determined graphically?
(a) Mean (b) Median (c) Mode (d) None of these Answer: (a) Mean Sol: The mean cannot be determined graphically because the values cannot be summed.
Which of the following is not a measure of central tendency?
(a) Mean (b) Mode (c) Median (d) Standard Deviation Answer: (d) Standard Deviation Sol: The standard deviation is a measure of dispersion. It is the action or process of distributing...
Calculate the missing frequency form the following distribution, it being given that the median of the distribution is 24.
The following table, construct the frequency distribution of the percentage of marks obtained by 2300 students in a competitive examination.
The following table gives the life-time (in days) of 100 electric bulbs of a certain brand.
The following frequency distribution gives the monthly consumption of electricity ofr 64 consumers of locality.
In the following data, find the values of p and q. Also, find the median class and modal class.
The following are the ages of 300 patients getting medical treatment in a hospital on a particular day:
Find the mode of the given data:
What is the cumulative frequency of the modal class of the following distribution?
If the median of ???? 5 , ???? 4 , ???? 2 , ???? and ???? 3 , where x > 0, is 8, find the value of x. Hint Arranging the observations in ascending order, we have ????/ 5 , ???? /4 , ????/ 3 , ????/ 2 , ???? Median= ????/ 3 = 8.
The median of 19 observations is 30. Two more observation are made and the values of these are 8 and 32. Find the median of the 21 observations taken together. Hint Since 8 is less than 30 and 32 is more than 30, so the value of median (middle value) remains unchanged.
Sol: Since, 8 is less than 30 and 32 is more than 30, so the middle value remains unchanged Thus, the median of 21 observations taken together is 30.
The observation 29, 32, 48, 50, x, x+2, 72, 78, 84, 95 are arranged in ascending order. What is the value of x if the median of the data is 63?arranged in ascending order. What is the value of x if the median of the data is 63?
In a frequency distribution table with 12 classes, the class-width is 2.5 and the lowest class boundary is 8.1, then what is the upper class boundary of the highest class?
Sol: Upper class boundary = Lowest class boundary + width × number of classes = 8.1 + 2.5×12 = 8.1 + 30 = 38.1 Thus, upper class boundary of the highest class is 38.1.
The distribution X and Y with total number of observations 36 and 64, and mean 4 and 3 respectively are combined. What is the mean of the resulting distribution X + Y?
While calculating the mean of a given data by the assumed-mean method, the following values were obtained.
Find the class marks of classes 10 -25 and 35 – 55.
Find the class marks of classes 10 -25 and 35 – 55.
In a class test, 50 students obtained marks as follows:
For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation.
A data has 25 observations arranged in a descending order. Which observation represents the median?
What is the lower limit of the modal class of the following frequency distribution?
Write the median class of the following distribution:
From the following data, draw the two types of cumulative frequency curves and determine the median:
The marks obtained by 100 students of a class in an examination are given below:
From the following frequency, prepare the ‘more than’ ogive.
The table given below shows the weekly expenditures on food of some households in a locality
The following table gives the production yield per hectare of wheat of 100 farms of a village.
The monthly consumption of electricity (in units) of some families of a locality is given in the following frequency distribution:
The heights of 50 girls of Class X of a school are recorded as follows:
Draw a ‘more than’ ogive for the data given below which gives the marks of 100 students.
The given distribution shows the number of wickets taken by the bowlers in one-day international cricket matches:
Find the median of the following data by making a ‘less than ogive’.
The table below shows the daily expenditure on food of 30 households in a locality:
The following table gives the daily income of 50 workers of a factory:
A survey regarding the heights (in cm) of 50 girls of a class was conducted and the following data was obtained:
Find the mean, median and mode of the following data:
Find the mean, median and mode of the following data:
Find the mean, median and mode of the following data:
Find the mean, median and mode of the following data:
The agewise participation of students in the annual function of a school is shown in the following distribution.
Compute the mode from the following data:
Compute the mode from the following series:
Compute the mode from the following data:
Calculate the mode from the following data:
Given below is the distribution of total household expenditure of 200 manual workers in a city:
Find the mode of the following distribution:
Heights of students of class X are givee in the flowing frequency distribution
Compute the mode of the following data:
Find the mode of the following distribution:
Find the median from the following data:
Find the median from the following data:
Find the median wages for the following frequency distribution:
Calculate the median for the following data:
If the median of the following frequency distribution is 32.5, find the values of f1 and f2.
In the following data the median of the runs scored by 60 top batsmen of the world in oneday international cricket matches is 5000. Find the missing frequencies x and yIn the following data the median of the runs scored by 60 top batsmen of the world in oneday international cricket matches is 5000. Find the missing frequencies x and yIn the following data the median of the runs scored by 60 top batsmen of the world in oneday international cricket matches is 5000. Find the missing frequencies x and y
The median of the following data is 16. Find the missing frequencies a and b if the total of frequencies is 70.
Calculate the missing frequency from the following distribution, it being given that the median of distribution is 24.
Calculate the median from the following data:
Given below is the number of units of electricity consumed in a week in a certain locality:
Calculate the median from the following frequency distribution table:
The following table shows the daily wages of workers in a factory:
Compute mean from the following data:
In a hospital, the ages of diabetic patients were recorded as follows. Find the median age.
The following table shows the marks scored by 80 students in an examination:
Weight of 60 eggs were recorded as given below:
The following table shows the age distribution of patients of malaria in a village during a particular month:
Find the mean age from the following frequency distribution:
Find the mean of the following data using step-deviation method:
Find the arithmetic mean of the following frequency distribution using step-deviation method:
In an annual examination, marks (out of 90) obtained by students of Class X in mathematics are given below:
Find the mean of the following frequency distribution table using a suitable method:
The weights of tea in 70 packets are shown in the following table:
Find the mean of the following data, using step-deviation method:
Find the mean of the following frequency distribution using step-deviation method.
The following table gives the literacy rate (in percentage) in 40 cities. Find the mean literacy rate, choosing a suitable method.
Find the mean of the following data, using assumed-mean method:
Find the mean of the following frequency distribution, using the assumed-mean method:
Find the mean marks per student, using assumed-mean method:
During a medical check-up, the number of heartbeats per minute of 30 patients were recorded and summarized as follows:
Find the mean of the following frequency distribution is 57.6 and the total number of observation is 50.
The daily expenditure of 100 families are given below. Calculate ????1 and ????2 if the mean daily expenditure is ₹ 188.
The mean of the following frequency data is 42, Find the missing frequencies x and y if the sum of frequencies is 100.
The mean of following frequency distribution is 54. Find the value of p.
The following distribution shows the daily pocket allowance of children of a locality. If the mean pocket allowance is ₹ 18 , find the missing frequency f.
If the mean of the following frequency distribution is 24, find the value of p.
Using an appropriate method, find the mean of the following frequency distribution:
Find the mean of the following data, using direct method:
Find the mean of the following data, using direct method:
Find the mean using direct method:
Compute the mean for following data:
If the mean of 25 observations is 27 and each observation is decreased by 7, what will be new mean?
If the mean of 5 observation x, x + 2, x + 4, x +6and x + 8 , find the value of x.
Mark the tick against the correct answer in the following: If the points 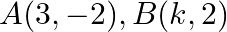 and
and 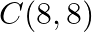 are collinear then the value of
are collinear then the value of 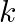 is
is
A. 2
B. 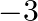
C. 5
D. 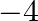
Solution: Option(C) To find: Area of $A B C$ Given: $A(3,-2), B(k, 2)$ and $C(8,8)$ The formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} &...
Mark the tick against the correct answer in the following: The solution set of the equation 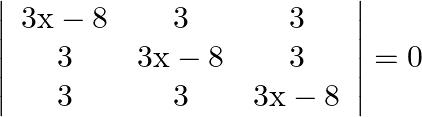 is
is
A. 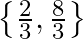
B. 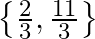
C. 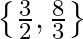
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8\end{array}\right|=0$ Applying $\mathrm{R}_{1}...
Mark the tick against the correct answer in the following: The solution set of the equation 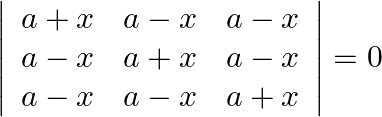 is
is
A. 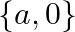
B. 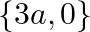
C. 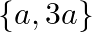
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 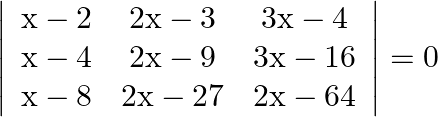 is
is
A. 
B. 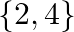
C. 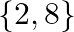
D. 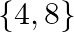
Solution: Option(A) To find: Value of $x$ We have, $\left|\begin{array}{ccc}x-2 & 2 x-3 & 3 x-4 \\ x-4 & 2 x-9 & 3 x-16 \\ x-8 & 2 x-27 & 3 x-64\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: If 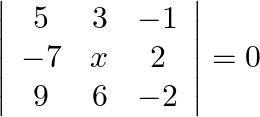 then
then 
A. 0
B. 6
C. 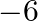
D. 9
Solution: Option(C) To find: Value of $\mathrm{x}$ We have, $\left|\begin{array}{ccc}5 & 3 & -1 \\ -7 & x & 2 \\ 9 & 6 & -2\end{array}\right|=0$ Applying $R_{1} \rightarrow 2...
Mark the tick against the correct answer in the following: 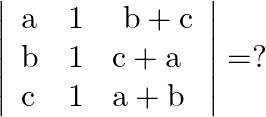
A. 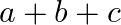
B. 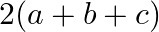
C. 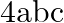
D. 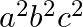
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}a & 1 & b+c \\ b & 1 & c+a \\ c & 1 & a+b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & 1 &...
Mark the tick against the correct answer in the following: 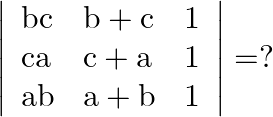
A. 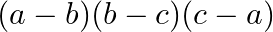
B. 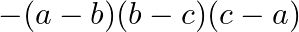
C. 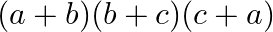
D. None of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\mathrm{bc} & \mathrm{b}+\mathrm{c} & 1 \\ \mathrm{ca} & \mathrm{a}+\mathrm{c} & 1 \\ \mathrm{ab} &...
Mark the tick against the correct answer in the following: 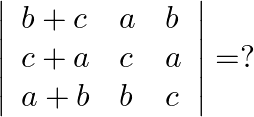
A. 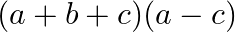
B. 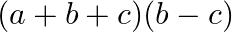
C. 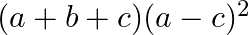
D. 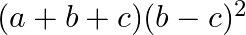
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}b+c & a & b \\ c+a & c & a \\ a+b & b & c\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 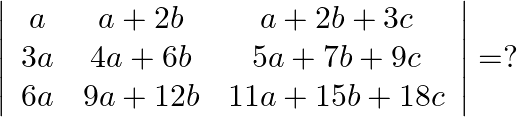
A. 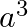
B. 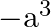
C. 0
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$ We...
Mark the tick against the correct answer in the following: 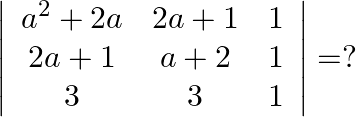
A. 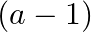
B. 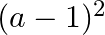
C. 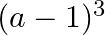
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}a^{2}+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 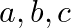 be distinct positive real numbers then the value of
be distinct positive real numbers then the value of 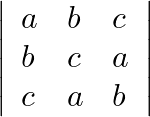 is
is
A. positive
B. negative
C. a perfect square
D. 0
Solution: Option(B) To find: Nature of $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & b & c \\...
Mark the tick against the correct answer in the following: 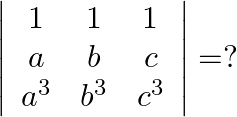
A. 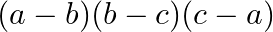
B. 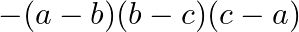
C. 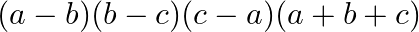
D. 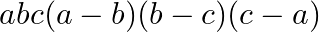
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{3} & b^{3} & c^{3}\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1...
Mark the tick against the correct answer in the following: 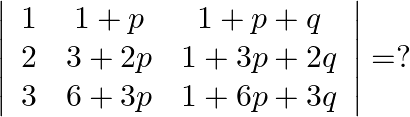
A. 0
B. 1
C. 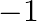
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 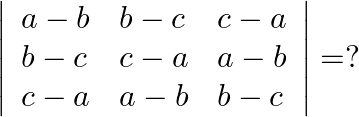
A. 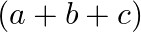
B. 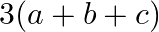
C. 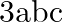
D. 0
Solution: Option(D) To find: Value of $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ We have, $\left|\begin{array}{lll}a-b...
Mark the tick against the correct answer in the following: 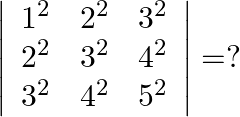
A. 8
B. 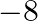
C. 16
D. 142
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2}\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 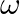 is a complex root of unity then
is a complex root of unity then 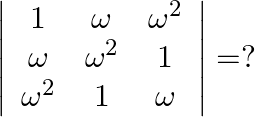
A. 1
B. 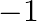
C. 0
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & \omega & \omega^{2} \\ \omega & \omega^{2} & 1 \\ \omega^{2} & 1 & \omega\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 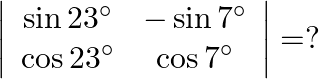
A. 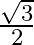
B. 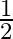
C. 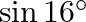
D. 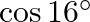
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\sin 23^{\circ} & -\sin 7^{\circ} \\ \cos 23^{\circ} & \cos 7^{\circ}\end{array}\right|$ Formula used: (i) $\sin (A+B)=\sin A...
Mark the tick against the correct answer in the following: 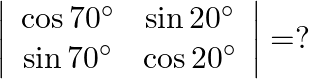
A. 1
B. 0
C. 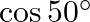
8D. 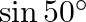
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\cos 70^{\circ} & \sin 20^{\circ} \\ \sin 70^{\circ} & \cos 20^{\circ}\end{array}\right|$ Formula used: (i) $\cos \theta=\sin...
Using binomial theorem, expand each of the following:
If the points 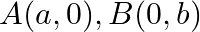 and
and 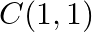 are collinear, prove that
are collinear, prove that 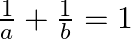
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If  and
and 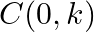 be three points such that area of a
be three points such that area of a 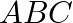 is 4 sq units, find the value of
is 4 sq units, find the value of 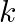 .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 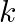 for which the area of a ABC having vertices
for which the area of a ABC having vertices 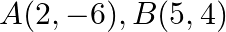 and
and 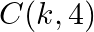 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 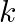 for which the points
for which the points 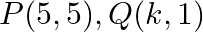 and
and 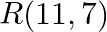 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 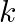 for which the points
for which the points 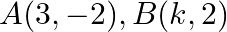 and
and 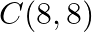 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 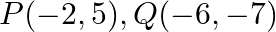 and
and 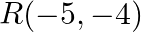
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 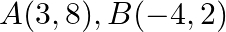 and
and 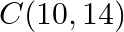
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 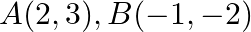 and
and 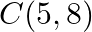
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 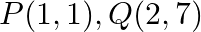 and
and 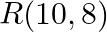
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 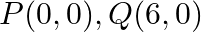 and
and 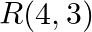
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 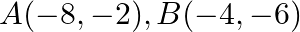 and
and 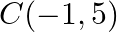
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 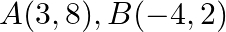 and
and 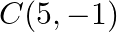
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Prove that 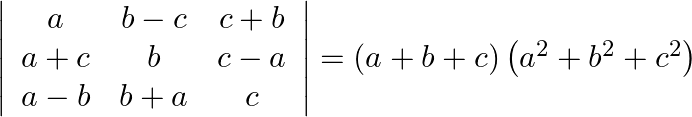
Solution: Operating $\mathrm{C}_{1} \rightarrow \mathrm{aCl}_{1}$ $=\frac{1}{a}\left|\begin{array}{ccc} a^{2} & b-c & c+b \\ a^{2}+a c & b & c-a \\ a^{2}-a b & b+a & c...
Solve the following equations: 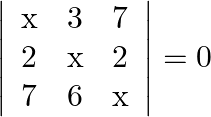
Solution: Operating $R 1 \rightarrow R 1+R_{2}+R_{3}$ $0=\left|\begin{array}{ccc} x+9 & x+9 & x+9 \\ 2 & x & 2 \\ 7 & 6 & x \end{array}\right|$ Taking $(x+9)$ common from...
Solve the following equations: 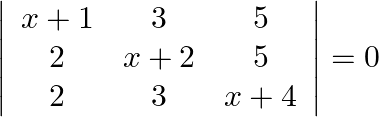
Solution: Operating $C_{1} \rightarrow C_{1}+C_{2}+C_{3}$ $0=\left|\begin{array}{ccc} x+9 & 3 & 5 \\ x+9 & x+2 & 5 \\ x+9 & 3 & x+4 \end{array}\right|$ Taking $(x+9)$ common...
Solve the following equations: 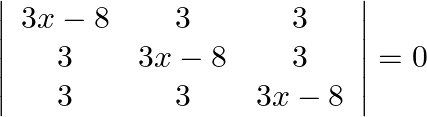
Solution: $\text { Operating } \mathrm{Cl} \rightarrow \mathrm{Cl}+\mathrm{C}_{2}+\mathrm{C}_{3}$ $0=\left|\begin{array}{ccc} 3 x-8+3+3 & 3 & 3 \\ 3+3 x-8+3 & 3 x-8 & 3 \\ 3+3+3 x-8...
Solve the following equations: 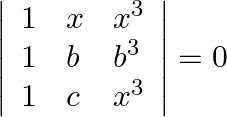
Solution: Operating $R 1 \rightarrow R 1^{-} R_{2}, R_{2 \rightarrow R 2}-R_{3}$ $\left|\begin{array}{ccc} 0 & x-b & x^{3}-b^{3} \\ 0 & b-c & b^{3}-c^{3} \\ 1 & c & c^{3}...
Show that 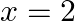 is a root of the equation
is a root of the equation 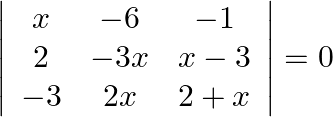 .
.
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}$ $\begin{aligned} 0 &=\left|\begin{array}{ccc} x-2 & -6+3 x & -1-x+3 \\ 2 & -3 x & x-3 \\ -3 & 2 x & 2+x...
Without expanding the determinant, prove that: 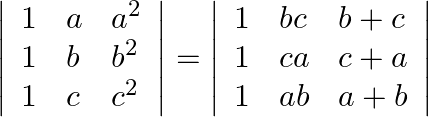
Solution: $\text { Operating } R 1 \rightarrow R 1^{-} R_{3}, R_{2 \rightarrow R_{2}-R 3}$ $\begin{array}{l} \left|\begin{array}{ccc} 0 & \mathrm{a}-\mathrm{c} &...
Without expanding the determinant, prove that: 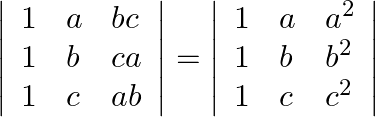
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\rightarrow\left|\begin{array}{ccc} 0 & \mathrm{a}-\mathrm{b} & \mathrm{b} c-\mathrm{ac} \\ 0 &...
Prove that 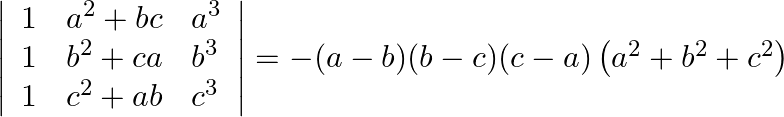
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\begin{array}{l} =\left|\begin{array}{ccc} 0 & \mathrm{a}^{2}+\mathrm{bc}-\mathrm{b}^{2}-\mathrm{ac} &...
If 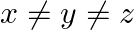 and
and 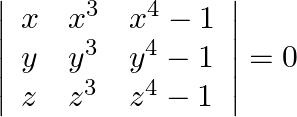 , prove that
, prove that 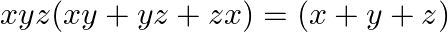
Solution: By properties of determinants, we can split the given determinant into 2 parts $\rightarrow 0=\left|\begin{array}{lll} \mathrm{x} & \mathrm{x}^{3} & \mathrm{x}^{4} \\ \mathrm{y}...
Using properties of determinants prove that: 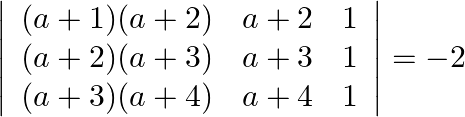
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\begin{array}{l} =\left|\begin{array}{ccc} (a+1)(a+2)-(a+2)(a+3) & a+2-a-3 & 0 \\ (a+2)(a+3)-(a+3)(a+4)...
Using properties of determinants prove that: 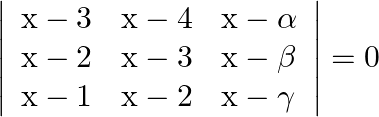 , where
, where 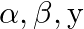 are in AP.
are in AP.
Solution: Given that $\alpha, \beta, \gamma$ are in an $A P$, which means $2 \beta=\alpha+\gamma$ Operating $R_{3} \rightarrow R_{3}-2 R_{2}+R_{1}$ $\begin{array}{l} =\left|\begin{array}{ccc} x-3...
Using properties of determinants prove that: 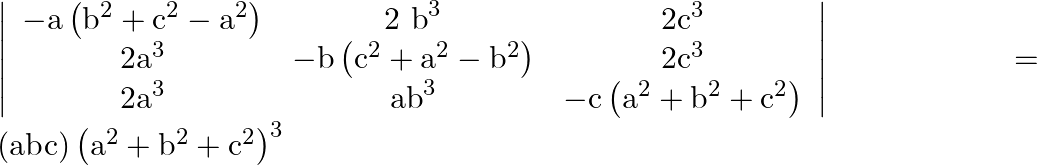
Solution: Taking $a, b, c$ from $C_{1}, C_{2}, C_{3}$ $=a b c\left|\begin{array}{ccc} -b^{2}-c^{2}+a^{2} & 2 b^{2} & 2 c^{2} \\ 2 a^{2} & b^{2}-c^{2}-a^{2} & 2 c^{2} \\ 2 a^{2} &...
PQ is a chord of length 16 cm of a circle of radius 10 cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
Or
A quadrilateral is drawn to circumscribe a circle. Prove that the sum of opposite sides are equal.
Two concentric circles are of radii 5 cm and 3 cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
Prove that the parallelogram circumscribing a circle, is a rhombus.
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
If two tangents are drawn to a circle from an external point, show that they subtend equal angles at the centre.
In the given figure, if AB = AC, prove that BE = CE.
Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Fill in the blanks.
(i) A line intersecting a circle in two distinct points is called a ………
(ii) A circle can have parallel tangents at the most …
(iii) The common point of a tangent to a circle and the circle is called the ………
(iv) A circle can have ….. tangents
Sol: A line intersecting a circle at two district points is called a secant A circle can have two parallel tangents at the most The common point of a tangent to a circle and the circle is called the...
Two tangents segments BC and BD are drawn to a circle with center O such that CBD 120. Prove that OB 2BC
In the given figure, PA and PB are two tangents form an externa point P to a circle with centre O. If PBA 65 , find the OAB and APB.
In the given figure, PA and PB are the tangents to a circle with centre O. Show that the points A, O, B, P are concyclic.
In the given figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7cm, CR = 3cm and AS=5cm, find x.
In the given figure, AD and AE are the tangents to a circle with centre O and BC touches the circle at F. If AE = 5 cm, then perimeter of ABC is
If tangents PA and PB from a point P to a circle with center O are drawn so that APB 80, then, POA?
If the angles between two radii of a circle is 130 , then the angle between the tangents at the ends of the radii is (a) 65 (b) 40 (c) 50 (d) 90
In the given figure, O is the center of a circle, PQ is a chord and the tangent PT at P makes an angle of 50 with PQ. Then, POQ ?
Which of the following statement is not true?
(a) A line which intersect a circle in tow points, is called secant of the circle.
(b)A line intersecting a circle at one point only, is called a tangent to the circle.
(c) The point at which a line touches the circle, is called the point of contact.
(d) A tangent to the circle can be drawn form a point inside the circle.
Answer: (d) A tangent to the circle can be drawn form a point inside the circle. Sol: A tangent to the circle can be drawn from a point Inside the circle. This statement is false because tangents...
Which of the following statements is not true?
(a) A tangent to a circle intersects the circle exactly at one point.
(b) The point common to the circle and its tangent is called the point of contact.
(c) The tangent at any point of a circle is perpendicular to the radius of the circle through the point of contact.
(d) A straight line can meet a circle at one point only.
Answer: (d) A straight line can meet a circle at one point only. Sol: A straight be can meet a circle at one point only This statement is not true because a straight line that is not a tangent but a...
