(i) $\mathrm{A}(5,-12)$ Let $A(0,0)$ be the origin $$ &A=\sqrt{(5-0)^{2}+(-12-0)^{2}}\\ $$ $$ \begin{aligned} &=\sqrt{(5)^{2}+(-12)^{2}} \\ &=\sqrt{25+144} \\ &=\sqrt{169} \\ &=13 \text { units }...
Find the distance of each of the following points from the origin: (i)
Find the distance between the points (iii) 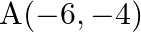 and
and 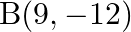 (iv)
(iv) 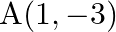 and
and 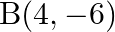
(iii) $\mathrm{A}(-6,-4)$ and $\mathrm{B}(9,-12)$ points are $\mathrm{A}(-6,-4)$ and $\mathrm{B}(9,-12)$ => $\left(x_{1}=-6, y_{1}=-4\right)$ and $\left(x_{2}=9, y_{2}=-12\right)$...
Find the distance between the points (i) 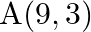 and
and 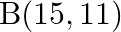 (ii)
(ii) 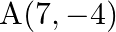 and
and 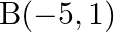
(i) $\quad \mathrm{A}(9,3)$ and $\mathrm{B}(15,11)$ The given points are $A(9,3)$ and $B(15,11)$. Then $\left(x_{1}=9, y_{1}=3\right)$ and $\left(x_{2}=15, y_{2}=11\right)$ $A...
State whether the following statements are true or false. Justify your answer. The points (0, 5), (0, –9) and (3, 6) are collinear.
Solution: The statement given in the question is false. Justification: If the area of a triangle formed by its points equals 0, then the points are collinear. Provided, ${{x}_{1}}~=\text{ }0,\text{...
State whether the following statements are true or false. Justify your answer. Point P (– 4, 2) lies on the line segment joining the points A (– 4, 6) and B (– 4, – 6).
Solution: The statement given in the question is true. Justification: Equation of the line conatining the points A and B using the two-point form is, $\frac{y-6}{x+4}=\frac{-6-6}{-4+4}$...
State whether the following statements are true or false. Justify your answer. △ABC with vertices A (–2, 0), B (2, 0) and C (0, 2) is similar to △DEF with vertices D (–4, 0) E (4, 0) and F (0, 4).
Solution: The statement given in the question is true. Justification: Distance formula, $d~=\text{ }\surd \text{ }({{({{x}_{2}}~\text{ }{{x}_{1}})}^{2}}~+\text{ }{{({{y}_{2}}~\text{...
ABCD is a rectangle formed by the points A (-1, – 1), B (-1, 4), C (5, 4) and D (5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Solution: The side AB has P as a mid-point, Coordinate of P = ( (-1 – 1)/2, (-1 + 4)/2 ) = (-1, 3/2) In the same way, Q, R, and S are (As Q is mid-point of BC, R is midpoint of CD and S is...
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ ABC.
(i) If A 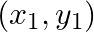 , B
, B 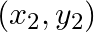 and C
and C 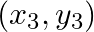 are the vertices of triangle ABC, find the coordinates of the centroid of the triangle.
are the vertices of triangle ABC, find the coordinates of the centroid of the triangle.
Solution: (i) If $A\left(x_{1}, y_{1}\right), B\left(x_{2}, y_{2}\right)$ and $C\left(x_{3}, y_{3}\right)$ are the vertices of triangle $A B C$, the coordinates of centroid can be given as...
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ ABC.
(i) The median from A meets BC at D. Find the coordinates of point D. (ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1. Solution: (i) D's coordinates can be computed using...
The vertices of a ∆ ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that AD/AB = AE/AC = 1/4. Calculate the area of the ∆ ADE and compare it with area of ∆ ABC. (Recall Theorem 6.2 and Theorem 6.6)
Given that: A (4, 6), B (1, 5) and C (7, 2) are the vertices of a ∆ABC. AD/AB = AE/AC = 1/4 AD/(AD + BD) = AE/(AE + EC) = 1/4 Points D and E divide AB and AC in a 1:3 ratio, respectively. D's...
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular lawn in the plot as shown in the fig. 7.14. The students are to sow the seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle. (ii) What will be the coordinates of the vertices of triangle PQR if C is the origin?Also calculate the areas of the...
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Solution: Let ABCD be a square with A(-1,2) and B(-1,2) (3,2). And Point O is the point where AC and BD intersect. Now find the coordinates of the points B and D. Step 1: Find coordinates of point O...
Find the centre of a circle passing through points (6, -6), (3, -7) and (3, 3).
Solution: The points on a circle are A = (6, -6), B = (3, -7), and C = (3, 3). OA = OB = OC if O is the centre. (radii are equal) If O is equal to (x, y), then OA = √[(x – 6)2 + (y + 6)2] OB = √[(x...
Find the relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution: The area of the triangle formed by the given points must be 0 if the points are collinear. Let the vertices of a triangle are (x, y), (1, 2) and (7, 0), The area of a triangle = 1/2 ×...
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, –2) and B(3, 7).
Solution: Consider how line 2x + y – 4 = 0 divides line AB in a k:1 ratio joined by the two points A(2, -2) and B(3, 7). The following are the coordinates of the point of division: x = (2 + 3k)/(k +...
You have studied in Class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, – 6), B (3, – 2) and C (5, 2).
Solution: Let A (4, -6), B (3, -2), and C (5, 2) be the vertices of the triangle. Let the side BC of triangle ABC has a midpoint as D. As a result, in ΔABC, AD is the median. Midpoint of BC =...
Find the area of the quadrilateral whose vertices, taken in order, are
(-4, -2), (-3, -5), (3, -2) and (2, 3). Solution: Let the quadrilateral's vertices be A (- 4, – 2), B (– 3, – 5), C (3, – 2), and D (2, 3). Divide the quadrilateral into two triangles by...
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution: Let the triangle's vertices be A (0, -1), B (2, 1), and C (3, 1). (0, 3). Let D, E, and F be the midpoints of the triangle's sides. D, E, and F coordinates are given by D .= (0+2/2, -1+1/2...
In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, -2), (5, 1), (3, -k) (ii) (8, 1), (k, -4), (2, -5) Solution: (i) The area of the triangle formed by collinear points is always zero. Let the vertices of a triangle be (7, -2) (5, 1), and (3,...
Find the area of the triangle whose vertices are:
(i) (2, 3), (-1, 0), (2, -4)<br> (ii) (-5, -1), (3, -5), (5, 2) Solution: The formula for calculating the area of a triangle is = 1/2 × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] (i) Given here,...
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order.[Hint: Area of a rhombus = 1/2 (product of its diagonals)
Solution: The vertices of a rhombus ABCD are A(3, 0), B (4, 5), C(– 1, 4) and D (– 2, – 1) Length of diagonal AC$=\sqrt{{{\left( 3-\left( -1 \right) \right)}^{2}}+{{\left( 0-4...
Find the coordinates of the points which divide the line segment joining A (- 2, 2) and B (2, 8) into four equal parts.
Solution: Make a figure, line dividing by 4 points. The points X, Y, and Z divide the line segment in the ratios 1:3, 1:1, and 3:1, respectively, as shown in the diagram. Coordinates of X$=\left(...
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.
Solution: Points A and B have coordinates of (-2,-2) and (2,-4) respectively. Because AP = 3/7, AB As a result, AP: PB = 3:4 The line segment AB is divided in 3:4 by point P. Coordinate of P...
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, – 3) and B is (1, 4).
Solution: Let's say point A's coordinates are (x, y). The midpoint of AB is (2, – 3), which is the circle's centre. Coordinate of B = (1, 4) (2, -3) =((x+1)/2 , (y+4)/2) (x+1)/2 = 2 and (y+4)/2 = -3...
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution: Let A,B,C and D be the points of a parallelogram as A(1, 2), B(4, y), C(x, 6) and D(3, 5). The midpoint of a parallelogram is the same since the diagonals bisect each other. To find...
Find the ratio in which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Solution: Let k : 1 be the ratio of the line segment connecting A (1, – 5) and B ( – 4, 5) divided by the x-axis. As a result, the coordinates of the division point, P(x, y), are ((-4k+1)/(k+1),...
Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).
Solution: Consider the ratio k :1 which connects the line segment ( -3, 10) and (6, -8) to the point ( -1, 6). As a result, -1 = ( 6k-3)/(k+1) –k – 1 = 6k -3 7k = 2...
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
We concluded from the given instructions that Niharika placed the green flag at 1/4th of the distance AD, or (1/4 ×100) m = 25 metres from the 2nd line's starting point. As a result, this...
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution: Let P (x1, y1) and Q (x2, y2) be the trisection points of the line segment joining the provided points, i.e. AP = PQ = QB. As a result, point P internally divides AB in the ratio 1:2....
Find the coordinates of the point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2:3.
Solution: Let the required point is P(x, y). Calculating using the section formula, we will get: x = (2×4 + 3×(-1))/(2 + 3) = (8 – 3)/5 = 1 y = (2×-3 + 3×7)/(2 + 3) = (-6 + 21)/5 = 3 As a result,...
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (- 3, 4).
Solution: (3, 6) and ( – 3, 4) are both equidistant from point (x, y). $\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}=\sqrt{{{\left( x-\left( -3 \right) \right)}^{2}}+{{\left( y-4...
If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also find the distance QR and PR.
Solution: Given: PQ = QR because Q (0, 1) is equidistant between P (5, – 3) and R (x, 6). Step 1: Using the distance formula, calculate the distance between PQ and QR. PQ$=\sqrt{{{\left( 5-0...
Find the values of y for which the distance between the points P (2, – 3) and Q (10, y) is 10 units.
Solution: Given: There is a distance of 10 between (2, – 3) and (10, y). Using the formula for distance, PQ$=\sqrt{{{\left( 10-2 \right)}^{2}}+{{\left( y+3 \right)}^{2}}}=\sqrt{{{\left( 8...
Find the point on the x-axis which is equidistant from (2, – 5) and (- 2, 9).
Solution: To locate a point on the x-axis. As a result, its y-coordinate will be zero. Let's say the x-axis point is (x,0). Consider the following : A = (x, 0), B = (2, – 5), and C = (- 2, 9)....
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (4, 5), (7, 6), (4, 3), (1, 2)
Solution: Let the vertices A, B, C, and D of the given quadrilateral be represented by the points (4, 5), (7, 6), (4, 3), and (1, 2), respectively. AB$=\sqrt{{{\left( 7-4 \right)}^{2}}+{{\left( 6-5...
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0) (ii) (- 3, 5), (3, 1), (0, 3), (- 1, – 4) Solution: (i) Let the points (- 1, – 2), (1, 0), ( – 1, 2), and ( – 3, 0) represent the quadrilateral's vertices...
In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
Solution: The coordinates of points A, B, C, and D are (3, 4), (6, 7), (9, 4) and (6, 1), respectively, as shown in the figure. Using the distance formula, we can calculate the distance between two...
Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Solution: Any isosceles triangle has two sides that are equal. We'll find the distance between all of the points to see if they're vertices of an isosceles triangle. Let the vertices A, B, and C be...
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution: All three points are collinear if the total of the lengths of any two line segments equals the length of the third line segment. Consider the following values, A = (1, 5) B = (2, 3)...
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
Solution: Consider the case of town A at point (0, 0). As a result, town B will be at the point (36, 15). The distance between the points (0, 0) and (36, 15) $d=\sqrt{{{(36-0)}^{2}}+{{\left( 15-0...
Find the distance between the following pairs of points:
(i) (a, b), (- a, – b) Solution: (i) Distance between (a, b), (-a, -b) $d=\sqrt{{{\left( -a-a \right)}^{2}}+{{\left( -b-b \right)}^{2}}}=\sqrt{{{\left( -2a \right)}^{2}}+{{\left( -2b \right)}^{2}}}$...
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1) (ii) (-5, 7), (-1, 3) Solutions: The distance formula, say d, is used to calculate the distance between two points (x1, y1) and (x2, y2), $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}}...
Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
We know that in an isosceles triangle, length of two sides is equal. We know that formula to find the distance (d) between two points $\left( {{x}_{1}},{{y}_{1}} \right)$and $\left(...
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
All three points are collinear if the total of the lengths of any two line segments equals the length of the third line segment. Consider the following values, A = (1, 5) B = (2, 3) and C = (-2,...
