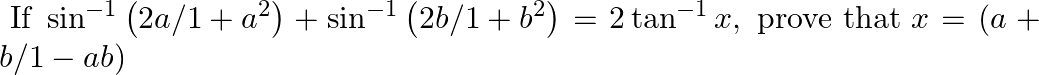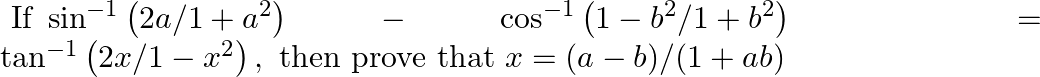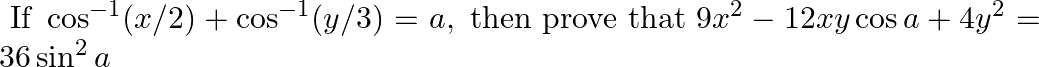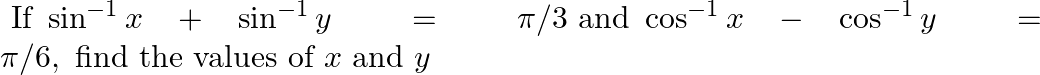Solution: $\begin{array}{l} f(n)=\left\{\begin{array}{l} \frac{1}{2}(n-1), \text { when } n \text { is odd } \\ -\frac{1}{2} n, \text { when } n \text { is even } \end{array}\right. \\ f(1)=0 \\...
Show that the function f:
The length of the hypotenuse of a right-angled triangle exceeds the length of the base by  and exceeds twice the length of the altitude by
and exceeds twice the length of the altitude by  . Find the length of each side of the triangle.
. Find the length of each side of the triangle.
Let the base and altitude of the right-angled triangle be $x$ and $y \mathrm{~cm}$, respectively Therefore, the hypotenuse will be $(x+2) \mathrm{cm}$. $\therefore(x+2)^{2}=y^{2}+x^{2}$ Again, the...
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
Let one side of the right-angled triangle be $x \mathrm{~m}$ and the other side be $(x+4) \mathrm{m}$. On applying Pythagoras theorem, we have: $\begin{array}{l} 20^{2}=(x+4)^{2}+x^{2} \\...
The area of right -angled triangle is 165 sq meters. Determine its base and altitude if the latter exceeds the former by 7 meters.
Let the base be $x \mathrm{~m}$. Therefore, the altitude will be $(x+7) m$ $\begin{array}{l} \text { Area of a triangle }=\frac{1}{2} \times \text { Base } \times \text { Altitude } \\ \therefore...
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
Let the altitude of the triangle be $x \mathrm{~m}$. Therefore, the base will be $3 x \mathrm{~m}$. $\begin{array}{l} \text { Area of a triangle }=\frac{1}{2} \times \text { Base } \times \text {...
Prove that the function  is one – one but not onto.
is one – one but not onto.
Solution: In the range of $\mathrm{N} \mathrm{f}(\mathrm{x})$ is monotonically increasing. $\therefore f(n)=n^{2}+n+1$ is one one. But Range of $f(n)=[0.75, \infty) \neq N($ codomain $)$ Thus,...
The area of a right triangle is 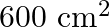 . If the base of the triangle exceeds the altitude by
. If the base of the triangle exceeds the altitude by 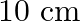 , find the dimensions of the triangle.
, find the dimensions of the triangle.
Let the altitude of the triangle be $x \mathrm{~cm}$ Therefore, the base of the triangle will be $(x+10) \mathrm{cm}$ $\begin{array}{l} \text { Area of triangle }=\frac{1}{2} x(x+10)=600 \\...
Show that the function
(i) 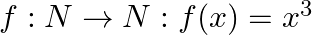 is one – one into
is one – one into
(ii) 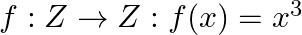 is one – one into
is one – one into
Solution: (i) $f: N \rightarrow N: f(x)=x^{3}$ is one - one into. $f(x)=x^{3}$ As the function $f(x)$ is monotonically increasing from the domain $N \rightarrow N$ $\therefore f(x)$ is one -one...
A farmer prepares rectangular vegetable garden of area 180 sq meters. With 39 meters of barbed wire, he can fence the three sides of the garden, leaving one of the longer sides unfenced. Find the dimensions of the garden.
Let the length and breadth of the rectangular garden be $x$ and $y$ meter, respectively. Given: $x y=180 \mathrm{sq} \mathrm{m}$$\ldots(i)$ and $\begin{array}{l} 2 y+x=39 \\ \Rightarrow x=39-2 y...
The length of a rectangle is thrice as long as the side of a square. The side of the square is 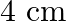 , more than the width of the rectangle. Their areas being equal, find the dimensions.
, more than the width of the rectangle. Their areas being equal, find the dimensions.
Let the breadth of rectangle be $x \mathrm{~cm}$. According to the question: Side of the square $=(x+4) \mathrm{cm}$ Length of the rectangle $=\{3(x+4)\} \mathrm{cm}$ It is given that the areas of...
The sum of the areas of two squares is 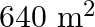 . If the difference in their perimeter be
. If the difference in their perimeter be 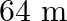 , find the sides of the two square
, find the sides of the two square
Let the length of the side of the first and the second square be $x$ and $y \cdot$ respectively. According to the question: $x^{2}+y^{2}=640$ Also, $\begin{array}{l} 4 x-4 y=64 \\ \Rightarrow x-y=16...
Show that the function
(i) 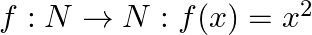 is one – one into.
is one – one into.
(ii) 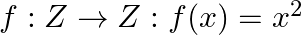 is many – one into
is many – one into
Solution: (i) $f: N \rightarrow N: f(x)=x^{2}$ is one - one into. As the function $f(x)$ is monotonically increasing from the domain $N \rightarrow N$ $\therefore f(x)$ is one -one Range of...
A rectangular filed in 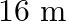 long and
long and 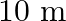 wide. There is a path of uniform width all around it, having an area of
wide. There is a path of uniform width all around it, having an area of 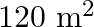 . Find the width of the path
. Find the width of the path
Let the width of the path be $x \mathrm{~m}$. $\therefore$ Length of the field including the path $=16+x+x=16+2 x$ Breadth of the field including the path $=10+x+x=10+2 x$ Now, (Area of the field...
The perimeter of a rectangular plot is  and its area is 288 sq meters. Find the dimension of the plot
and its area is 288 sq meters. Find the dimension of the plot
Let the length and breadth of the rectangular plot be $x$ and $y$ meter, respectively. Therefore, we have: $\begin{array}{l} \text { Perimeter }=2(x+y)=62 \quad \ldots . .(i) \text { and } \\ \text...
Let ![Rendered by QuickLaTeX.com f:\left[0, \frac{\pi}{2}\right] \rightarrow R: f(x)=\sin x](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-902634cb75410b73f743099ea343b78d_l3.png) and
and ![Rendered by QuickLaTeX.com g:\left[0, \frac{\pi}{2}\right] \rightarrow R: g(x)=\cos x](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5d08fed556b082ab80b726e70e9cca27_l3.png) . Show that each one of
. Show that each one of 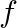 and
and 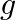 is one one but
is one one but 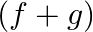 is not one – one.
is not one – one.
Solution: $f: \left[0, \frac{\pi}{2}\right] \rightarrow \mathrm{R}$ for given function $\mathrm{f}(\mathrm{x})=\sin$ Recalling the graph for $\sin \mathrm{x}$, we realise that for any two values on...
The length of a hall is 3 meter more than its breadth. If the area of the hall is 238 sq meters, calculate its length and breadth.
Let the breath of the rectangular hall be $x$ meter. Therefore, the length of the rectangular hall will be $(x+3)$ meter. According to the question: $\begin{array}{l} x(x+3)=238 \\ \Rightarrow...
The length of a rectangular field is three times its breadth. If the area of the field be 147 sq meters, find the length of the field.
Let the length and breadth of the rectangle be $3 x \mathrm{~m}$ and $x \mathrm{~m}$, respectively. According to the question: $\begin{array}{l} 3 x \times x=147 \\ \Rightarrow 3 x^{2}=147 \\...
The length of rectangle is twice its breadth and its areas is 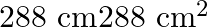 . Find the dimension of the rectangle.
. Find the dimension of the rectangle.
Let the length and breadth of the rectangle be $2 x \mathrm{~m}$ and $x \mathrm{~m}$, respectively. According to the question: $\begin{array}{l} 2 x \times x=288 \\ \Rightarrow 2 x^{2}=288 \\...
Two water taps together can fill a tank in 6 hours. The tap of larger diameter takes 9 hours less than the smaller one to fill the tank separately. Find the time which each tap can separately fill the tank.
Let the tap of smaller diameter fill the tank in $x$ hours. $\therefore$ Time taken by the tap of larger diameter to fill the tank $=(x-9) h$ Suppose the volume of the tank be $V$. Volume of the...
Show that the function 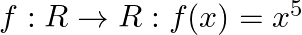 is one – one and onto.
is one – one and onto.
Solution: We need to show that $f: R \rightarrow R$ given by $f(x)=x s$ is one-one and onto. A function which is onto has every element of co-domain mapped to the at least one element of Domain....
Two pipes running together can fill a tank in 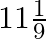 minutes. If on pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
minutes. If on pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
Let the time taken by one pipe to fill the tank be $x$ minutes. $\therefore$ Time taken by the other pipe to fill the tank $=(x+5) \min$ Suppose the volume of the tank be $V$. Volume of the tank...
Show that the function 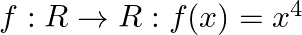 is many – one and into.
is many – one and into.
Solution: We need to show that f: $\mathrm{R} \rightarrow \mathrm{R}$ given by $\mathrm{f}(\mathrm{x})=\mathrm{x} 4$ is many-one into. A function which is not onto is into. A function where more...
Two pipes running together can fill a cistern in 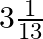 minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.
minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.
Let one pipe fills the cistern in $x$ mins. Therefore, the other pipe will fill the cistern in $(x+3)$ mins. Time taken by both, running together, to fill the cistern $=3 \frac{1}{13} \min...
A takes 10 days less than the time taken by  to finish a piece of work. If both
to finish a piece of work. If both  and
and  together can finish the work in 12 days, find the time taken by B to finish the work.
together can finish the work in 12 days, find the time taken by B to finish the work.
Let B takes $x$ days to complete the work. Therefore, A will take $(x-10)$ days. $\begin{array}{l} \therefore \frac{1}{x}+\frac{1}{(x-10)}=\frac{1}{12} \\ \Rightarrow...
A motorboat whose speed is 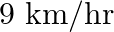 in still water, goes
in still water, goes 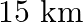 downstream and comes back in a total time of 3 hours 45 minutes. Find the speed of the stream.
downstream and comes back in a total time of 3 hours 45 minutes. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Downstream speed $=(9+x) \mathrm{km} / \mathrm{hr}$ Upstream speed $=(9-x) \mathrm{km} / \mathrm{hr}$ Distance covered...
The speed of a boat in still water is 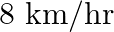 . It can go
. It can go 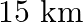 upstream and
upstream and 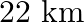 downstream is 5 hours. Fid the speed of the stream.
downstream is 5 hours. Fid the speed of the stream.
Speed of the boat in still water $=8 \mathrm{~km} / \mathrm{hr}$. Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Speed upstream $=(8-x) \mathrm{km} / \mathrm{hr}$ Speed...
Show that the function 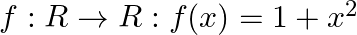 is many – one into.
is many – one into.
Solution: We need to show that $f: R \rightarrow R$ given by $f(x) = 1 + x^2$ is many-one into. A function which is not onto is into. A function where more than one element in Set A maps to one...
Let 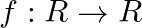 be defined by
be defined by 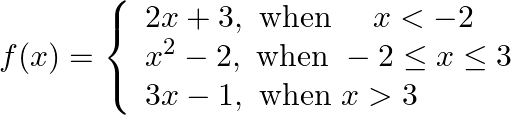
Find (i) 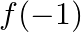 (ii)
(ii) 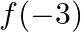 .
.
Solution: (i) $\mathrm{f}(-1)$ $x=-1$, it is satisfying the condition $-2 \leq x \leq 3$ Therefore, $f(x)=x_{2}-2$ $\begin{aligned} \begin{aligned} \therefore \mathrm{f}(-1) =(-1)_{2}-2 \\ =1-2 \\...
A motor boat whose speed in still water is 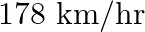 , takes 1 hour more to go
, takes 1 hour more to go 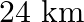 upstream than to return to the same spot. Find the speed of the stream.
upstream than to return to the same spot. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. Given: Speed of the boat $=18 \mathrm{~km} / \mathrm{hr}$ $\therefore$ Speed downstream $=(18+x) \mathrm{km} / h r$ Speed upstream...
The distance between Mumbai and Pune is 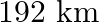 . Travelling by the Deccan Queen, it takes 48 minutes less than another train. Calculate the speed of the Deccan Queen if the speeds of the two train differ by
. Travelling by the Deccan Queen, it takes 48 minutes less than another train. Calculate the speed of the Deccan Queen if the speeds of the two train differ by 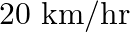
Let the speed of the Deccan Queen be $x \mathrm{~km} / \mathrm{hr}$. According to the question: Speed of another train $=(x-20) \mathrm{km} / \mathrm{hr}$ $\begin{array}{l} \therefore...
A passenger train takes 2 hours less for a journey of 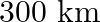 if its speed is increased by
if its speed is increased by 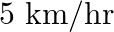 from its usual speed. Find its usual speed.
from its usual speed. Find its usual speed.
Let the usual speed $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\begin{array}{l} \frac{300}{x}-\frac{300}{(x+5)}=2 \\ \Rightarrow \frac{300(x+5)-300 x}{x(x+5)}=2 \\ \Rightarrow...
Let 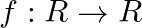 be defined by
be defined by 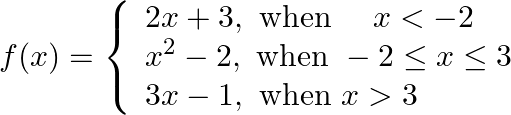
Find (i) 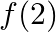 (ii)
(ii) 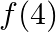
Solution: (i) $\mathrm{f}(2)$ $x=2$, it is satisfying the condition $-2 \leq x \leq 3$ Therefore, $f(x)=x_{2}-2$ $\begin{aligned} \therefore \mathrm{f}(2) =22-2 \\ =4-2 \\ =2 \\ \therefore...
A train covers a distance of 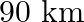 at a uniform speed. Had the speed been
at a uniform speed. Had the speed been 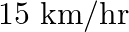 more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Let the original speed of the train be $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\frac{90}{x}-\frac{90}{(x+15)}=\frac{1}{2}$ $\begin{array}{l} \Rightarrow \frac{90(x+15)-90...
Give an example of a function which is
(i) neither one – one nor onto
(ii) onto but not one – one.
Solution: (i) Neither one-one nor onto $\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}$ given by $\mathrm{f}(\mathrm{x})=|\mathrm{x}|=\left\{\begin{array}{l}\mathrm{x}, \text { if } \mathrm{x} \geq 0...
A train travels 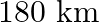 at a uniform speed. If the speed had been
at a uniform speed. If the speed had been 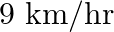 more, it would have taken 1 hour less for the same journey. Find the speed of the train.
more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Let the speed of the train be xkmph The time taken by the train to travel $180 \mathrm{~km}$ is $\frac{180}{\mathrm{x}} \mathrm{h}$ The increased speed is $\mathrm{x}+9$ The time taken is...
Give an example of a function which is
(i) one – one but not onto
(ii) one – one and onto
Solution: (i) One-One but not Onto $\mathrm{f}: \mathrm{N} \rightarrow \mathrm{N}$ be a mapping given by $\mathrm{f}(\mathrm{x})=\mathrm{x} 2$ For one-one $\begin{array}{l} f(x)=f(y) \\ x_{2}=y z \\...
A train travels at a certain average speed for a distanced of 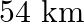 and then travels a distance of 63
and then travels a distance of 63 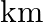 at an average speed of
at an average speed of 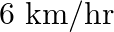 more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Let the first speed of the train be $x \mathrm{~km} / \mathrm{h}$. Time taken to cover $54 \mathrm{~km}=\frac{54}{x} h .$ New speed of the train $=(x+6) \mathrm{km} / \mathrm{h}$ $\therefore$ Time...
A train covers a distance of 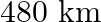 at a uniform speed. If the speed had been
at a uniform speed. If the speed had been 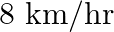 less then it would have taken 3 hours more to cover the same distance. Find the usual speed of the train.
less then it would have taken 3 hours more to cover the same distance. Find the usual speed of the train.
Let the usual speed of the train be $x \mathrm{~km} / \mathrm{h}$. $\therefore$ Reduced speed of the train $=(x-8) \mathrm{km} / \mathrm{h}$ Total distance to be covered $=480 \mathrm{~km}$ Time...
Define each of the following:
(i) bijective function
(ii) many – one function
Give an example of each type of functions.
Solution: (i)Bijective function: It is, also known as one-one onto function and is a function where for every element of set A, there is exactly one image in set B, such that no element is set B is...
Define a function. What do you mean by the domain and range of a function? Give examples.
Solution: A function is stated as the relation between the two sets, where there is exactly one element in set B, for every element of set A. A function is represented as f: A → B, which means ‘f’...
Let A = (1, 2, 3, 4) and R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (1, 3), (3, 2)}. Show that R is reflexive and transitive but not symmetric.
Solution: $\begin{array}{l} \mathrm{A}=\{1,2,3,4\} \text { and } \mathrm{R}=\{(1,1),(2,2),(3,3),(4,4),(1,2),(1,3) \\ (3,2)\} \text { (Given) } \end{array}$ $\mathrm{R}$ is reflexive if $\mathrm{a}...
Let A = {1, 2, 3} and R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}. Show that R is reflexive but neither symmetric nor transitive.
Solution: $A=\{1,2,3\}$ and $\bar{R}=\{(1,1),(2,2),(3,3),(1,2),(2,3)\}$ (Given) $\mathrm{R}$ is reflexive if $\mathrm{a} \in \mathrm{A}$ and $(\mathrm{a}, \mathrm{a}) \in \mathrm{R}$ Here,...
Let 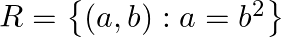 for all
for all 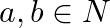 Show that R satisfies none of reflexivity, symmetry and transitivity.
Show that R satisfies none of reflexivity, symmetry and transitivity.
Solution: $\mathrm{R}=\left\{(\mathrm{a}, \mathrm{b}): \mathrm{a}=\mathrm{b}_{2}\right\}$ for all $\mathrm{a}, \mathrm{b} \in \mathrm{N}$ (As given) Non-Reflexivity: Assume $a$ be an arbitrary...
Let S be the set of all points in a plane and let R be a relation in S defined by R = {(A, B) : d(A, B) < 2 units}, where d(A, B) is the distance between the points A and B. Show that R is reflexive and symmetric but not transitive.
Solution: $\mathrm{R}=\{(\mathrm{A}, \mathrm{B}): \mathrm{d}(\mathrm{A}, \mathrm{B})<2$ units $\}$, where $\mathrm{d}(\mathrm{A}, \mathrm{B})$ is the distance between the points $\mathrm{A}$ and...
Show that the relation 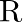 on
on  , defined by
, defined by 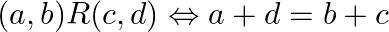 is an equivalent relation.
is an equivalent relation.
Solution: If $R$ is Reflexive, Symmetric and Transitive, then $R$ is an equivalence relation. Reflexivity: Suppose $a$ and $\mathrm{b}$ be an arbitrary element of $\mathrm{N} \times \mathrm{N}$...
Let 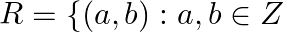 and
and 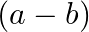 is divisible by 5
is divisible by 5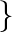 Show that
Show that 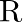 is an equivalence relation on
is an equivalence relation on 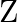 .
.
Solution: $\mathrm{R}=\{(\mathrm{a}, \mathrm{b}): \mathrm{a}, \mathrm{b} \in \mathrm{Z}$ and $(\mathrm{a}-\mathrm{b})$ is divisible by 5$\}$ (As given) If $R$ is Reflexive, Symmetric and Transitive,...
Let  be the set of all triangles in a plane. Show that the relation
be the set of all triangles in a plane. Show that the relation 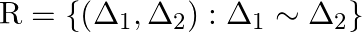 is an equivalence relation on
is an equivalence relation on 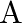 .
.
Solution: Suppose $\mathrm{R}=\left\{\left(\Delta 1, \Delta_{2}\right): \Delta_{1} \sim \Delta_{2}\right\}$ be a relation defined on A. (As given) If $\mathrm{R}$ is Reflexive, Symmetric and...
Given 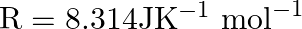 , the work done during combustion of
, the work done during combustion of 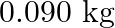 of ethane (molar mass
of ethane (molar mass 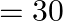 ) at
) at 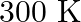 is A)
is A) 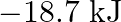 B)
B) 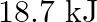 C)
C) 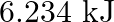 D)
D) 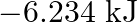
Correct option is B $18.7 \mathrm{~kJ}$ $ \begin{array}{l} \mathrm{C}_{2} \mathrm{H}_{6(\mathrm{~g})}+\frac{7}{2} \mathrm{O}_{2(\mathrm{~g})} \longrightarrow...
On the set S of all real numbers, define a relation R = {(a, b) : a ≤ b}. Show that R is
(i) reflexive
(ii) transitive
Solution: (i) Reflexivity: Suppose $\mathrm{p}$ is an arbitrary element of $\mathrm{S}$. So now, $\mathrm{p} \leq \mathrm{p}$ $\Rightarrow(p, p) \in R$ Therefore, $\mathrm{R}$ is reflexive. (ii)...
Let S be the set of all sets and let R = {(A, B) : A ⊂ B)}, i.e., A is a proper subset of B. Show that R is
(i) not symmetric.
Solution: (i) $A \subset B$ and $(A, B) \in R$ (As given) i.e. $\mathrm{A}$ is a proper subset of $\mathrm{B}$ But, B cannot be a proper subset of A Since, B can contain atleast one element that is...
Which among the following functional groups has been given the highest priority while assigning R-S configuration? A) 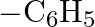 B)
B) 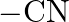 C)
C) 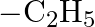 D)
D) 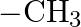
Correct option is B Explanation: Because -CN has the highest atomic number, the atom with the highest atomic number that is immediately linked to carbon will be seen first, followed by the remaining...
Let R = {(a, b) : a, b ∈ N and b = a + 5, a < 4}. Find the domain and range of R.
Solution: Since a< 4, $a = 1, 2, 3$ Therefore, R $=$ {(1, 6), (2, 7), (3, 8)} As a result, Domain(R) = {1, 2, 3} and Range(R) = {6, 7, 8}
Let 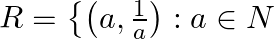 and
and 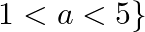 . Find the domain and range of
. Find the domain and range of 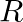 .
.
Solution: Since 1<a< 5, $a = 2, 3, 4$ Therefore, R $= {\{(2,{\frac12}), (3,{\frac13}), (4,{\frac14})}\}$ As a result, Domain(R) = {2, 3, 4} and Range(R) =...
Let R = {(a, b) : b = |a – 1|, a ∈ Z and la| < 3}. Find the domain and range of R.
Solution: As $|a| < 3$, $a = −2$, $−1$, $0$, $1$, $2$ Therefore, R = {(−2, 3), (−1, 2), (0, 1), (1, 0), (2, 1)} As a result, Domain(R) = {-2, -1, 0, 1, 2} and Range(R) = {3, 2, 1, 0}
Let R = (x, y) : x + 2y = be are relation on N. Write the range of R.
Solution: $x + 2y = 8$ (given) $x = 8 – 2y$ Putting $y = 1$ $x = 8 – 2(1) = 6$ Putting $y = 2$ $x = 8 – 2(2) = 4$ Putting $y = 3$ $x = 8 – 2(3) = 2$ Putting $y = 4$ $x = 8 – 2(4) = 0$; which is not...
Let R = {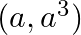 : a is a prime number less than 5}. Find the range of R.
: a is a prime number less than 5}. Find the range of R.
Solution: R = {(2, 8), (3, 27) Therefore, Range of R = {8 27}
Find the domain and range of the relation
R = {(-1, 1), (1, 1), (-2, 4), (2, 4)}.
Solution: Set of all the first elements or $x$-coordinates of the ordered pairs is called Domain. Set of all the second elements or $y$-coordinates of the ordered pairs is called Range. Therefore,...
Which among the following group 15 element forms most stable pentavalent compound? A) Phosphorus B) Antimony C) Bismuth D) Arsenic
Correct option is A Explanation: Because of the availability of d-electrons, phosphorus is a 15th group element that forms the most stable pentavalent compound. The stability of the +5 oxidation...
The process in which metal surface is made inactive is called A) Passivation B) Galvanizing C) Corrosion D) Pickling
Correct option is A Explanation: Passivation is the process of rendering a metal surface inert. Metal is treated with high oxidising chemicals, such as concentrated nitric acid, in this procedure....
What is the volume of water consumed during acid hydrolysis of 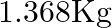 of sucrose? (Given
of sucrose? (Given  molar masses of sucrose
molar masses of sucrose 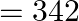 , water
, water 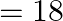 , density of water
, density of water 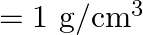 ) A)
) A) 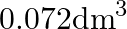 B)
B) 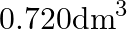 C)
C) 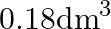 D)
D) 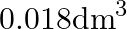
Correct option is A ($0.072 \mathrm{dm}^{3}$) $ \mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}+\mathrm{H}_{2} \mathrm{O} \stackrel{\mathrm{H}^{+}}{\longrightarrow} \mathrm{C}_{6} \mathrm{H}_{12}...
The correct order of reactivity of aldehydes and ketones towards hydrogen cyanide is A) 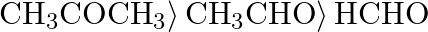 B)
B) 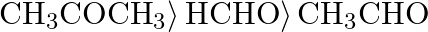 C)
C) 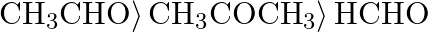 D)
D) 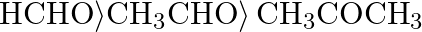
Correct option is D) $\left.\mathrm{HCHO}\rangle \mathrm{CH}_{3} \mathrm{CHO}\right\rangle \mathrm{CH}_{3} \mathrm{COCH}_{3}$ The following is the right order of reactivity of aldehydes and ketones...
What is the basicity of orthophosphorus acid ? A) One B) Two C) Three D) Four
B is the correct answer The basicity of orthophosphorous acid is two due to the presence of two - OH groups in its structure.
Identify the heteropolymer from the list given below. A) Polythene B) Nylon-6 C) Teflon D) Nylon-6, 6
D is the correct answer (Nylon-6, 6) A heteropolymer is one that is made up of two or more distinct (though often related) monomers. Hexamethylenediamine and adipic acid, which give nylon 66 its...
What is the chemical composition of Nicol’s prism? A) 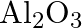 B)
B) 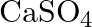 C)
C) 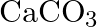 D)
D) 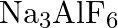
Correct option is C Explanation: A Nicol prism is a type of polarizer, which is an optical device that produces a polarised light beam. It is constructed in such a way that total internal reflection...
Identify a metalloid from the following list of elements. A) Carbon B) Neon C) Sodium D) Tellurium
Correct option is D Explanation: Tellurium is a silvery-white metalloid that possesses both metal and non-metal characteristics. Sodium is a metal, while carbon and neon are non-metals. As a result,...
Select a ferromagnetic material from the followings. A) Dioxygen B) Chromium (IV) oxide C) Benzene D) Dihydrogen monoxide
Correct option is B Explanation: Chromium (IV) dioxide is a ferromagnetic substance. These compounds' ferromagnetic properties allow them to be employed in data tapes, which are used to store data....
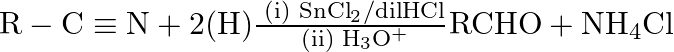 this reaction is known as A) Etard reaction B) Stephen reaction C) Hell-Vohlard-Zelinsky reaction D) Balz-Schiemann reaction
this reaction is known as A) Etard reaction B) Stephen reaction C) Hell-Vohlard-Zelinsky reaction D) Balz-Schiemann reaction
B is the correct answer. Explanation: Using tin chloride and dilution, aldehydes (R-CHO) are synthesised from nitriles (R-CN). Stephen's reaction is the reaction of HCl in an acidic media. As an...
For the reaction 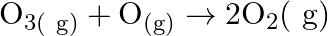 if the rate law expression is, rate
if the rate law expression is, rate ![Rendered by QuickLaTeX.com =\mathrm{K}\left[\mathrm{O}_{3}\right][\mathrm{O}]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e69a8d7ed909b9b87bef5e92873c3d1c_l3.png) the molecularity and order of the reaction are respectively A) 2 and 2 B) 2 and
the molecularity and order of the reaction are respectively A) 2 and 2 B) 2 and  C) 2 and 1 D) 1 and 2
C) 2 and 1 D) 1 and 2
Correct option is A (2 and 2) Rate $=\mathrm{K}\left[\mathrm{O}_{3}\right][\mathrm{O}]$ Order $=1+1=2$ Hence, the overall order of the reaction is 2 . Now, $ \mathrm{O}_{3(9)}+\mathrm{O}_{(9)}...
![Rendered by QuickLaTeX.com \left[\mathrm{Cr}\left(\mathrm{NH}_{3}\right)_{6}\right]\left[\mathrm{Cr}(\mathrm{SCN})_{6}\right] \text { and }\left[\mathrm{Cr}\left(\mathrm{NH}_{3}\right)_{2}(\mathrm{SCN})_{4}\right]\left[\mathrm{Cr}\left(\mathrm{NH}_{3}\right)_{4}(\mathrm{SCN})_{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1c51c7d9e0fc5c8f37f7a46ee940d288_l3.png) are the examples of what type of isomerism ? A) Ionisation isomerism B) Linkage isomerism C) Coordination isomerism D) Solvate isomerism
are the examples of what type of isomerism ? A) Ionisation isomerism B) Linkage isomerism C) Coordination isomerism D) Solvate isomerism
Correct option is C (Coordination isomerism) Explanation: The above examples are of coordination isomerism. It is because there are two coordination spheres in a compound.
For which among the following reactions, change in entropy is less than zero ? A) Sublimation of Iodine B) Dissociation of Hydrogen C) Formation of water D) Thermal decomposition of Calcium Carbonate
Correct option is B Explanation: The change in entropy during hydrogen dissociation is less than zero, which indicates it is negative. Hydrogen dissociation is a non-spontaneous process. As a...
The only radioactive element among the lanthanoids is A) Gadolinium B) Holmium C) Promethium D) Neodynium
Correct option is C Explanation: Promethium (Pm) is a lanthanoid element with the atomic number 61 and the symbol Pm. Its isotopes are all radioactive. Lanthanoids such as gadolinium, holmium, and...
The overall reaction taking place at anode during electrolysis of fused sodium chloride using suitable electrode is A) Oxidation of chloride B) Reduction of sodium ions C) Reduction of chlorine D) Oxidation of Sodium atoms
Correct option is A During the electrolysis of fused sodium chloride with a suitable electrode, the chloride ion is oxidised at the anode. Chloride ions are oxidised to chlorine gas by giving up...
What is the most abundant element on earth ? A) Hydrogen B) Nitrogen C) Oxygen D) Silicon
Correct option is C Explanation: Silicate minerals make up more than 90% of the earth's crust. Feldspars and alkali feldspar are the most common silicates. Other common silicate minerals include...
Diethyl amine when treated with nitrous acid yields A) Diethyl ammonium nitrite B) Ethyl alcohol C) N-nitroso diethyl amine D) Triethyl ammonium nitrite
Correct option is C) N-nitroso diethyl amine Explanation: N-nitroso diethylamine is formed by treating diethylamine with nitrous acid. It's a strong carcinogen.
Potassium dichromate is a good oxidizing agent, in acidic medium the oxidation state of chromium changes by A) 2 B) 3 C) 4 D) 5
Correct option is B Explanation: Dichromate oxidizes to $\mathrm{Cr}^{+3}$ from $\mathrm{Cr}_{2} \mathrm{O}_{7}^{-2}$ in acidic medium according to the reaction $ \mathrm{Cr}_{2}...
Which metal among the followings has the highest packing efficiency ? A) Iron B) Tungsten C) Aluminium D) Polonium
Correct option is C Explanation: The packing efficiency is the fraction of volume occupied by constituent particles in a crystal structure (volume of space occupied by the spheres/total volume). The...
Which of the following compounds has highest boiling point ? A) Propan-1-ol B) n-Butane C) Chloroethane D) Propanal
Correct option is A) Propan-1-ol Explanation: Hydrogen bonds have the potential to occur in propan-1-ol. Because of the strongly E.N oxygen atom, intermolecular hydrogen bonding develop in...
How is ore of aluminium concentrated ? A) roasting B) leaching C) froth floatation D) using Wilfley table
B is the correct answer. Explanation: The leaching method concentrates aluminium ore. Impurities in aluminium ore include SiO2, iron oxides, and titanium oxide. The powdered ore is digested with a...
Which of the following compounds is most acidic in nature ? A) 4-Chlorobutanoic acid B) 3-Chlorobutanoic acid C) 2-Chlorobutanoic acid D) Butanoic acid
The correct answer is C(2-chlorobutanoic acid) In nature, 2-chlorobutanoic acid is the most acidic. Because there is an electron withdrawing group (Cl) next to the carboxylic acid group (COOH). As a...
Van’t Hoff factor of centimolal solution of ![Rendered by QuickLaTeX.com \mathrm{K}_{3}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a99adc5c7be224b196c9e2507b50069e_l3.png) is
is 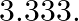 Calculate the percent dissociation of
Calculate the percent dissociation of ![Rendered by QuickLaTeX.com \mathrm{K}_{3}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a99adc5c7be224b196c9e2507b50069e_l3.png) A)
A) 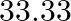 B)
B) 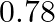 C) 78 D)
C) 78 D) 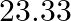
Correct option is C Explanation: $ \mathrm{K}_{3}\left[\mathrm{Fe}(\mathrm{CN})_{6}\right] \rightarrow 3 \mathrm{~K}^{+}+\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{3-} $ $ \mathrm{i}=\alpha...
Replacement of diazonium group by fluorine is known as A) Gattermann reaction B) Sandmeyer reaction C) Balz-Schiemann reaction D) Etard reaction
Correct option is C Balz-Schiemann reaction Explanation: The Balz- Schiemann reaction is a chemical reaction in which anilines are transformed to aryl fluorides via diazonium fluoroborates....
If 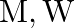 and
and 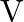 represent molar mass of solute, mass of solute and volume of solution in litres respectively, which among following equations is true? A)
represent molar mass of solute, mass of solute and volume of solution in litres respectively, which among following equations is true? A) 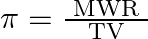 B)
B) 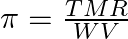 C)
C) 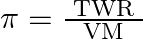 D)
D) 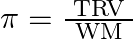
Correct option is C $\pi=\frac{\mathrm{TWR}}{\mathrm{VM}}$ $\pi=$ CRT where $\mathrm{C}$ is the concentration $\mathrm{C}=\frac{\text { Moles of solute }}{\text { volume }}$...
The correct IUPAC name of ![Rendered by QuickLaTeX.com \left[\mathrm{CO}\left(\mathrm{NH}_{3}\right)_{3}\left(\mathrm{NO}_{2}\right)_{3}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a87a614704284e544285de047b62719a_l3.png) A) Triammine trinitrito – N cobalt (III) B) Triammine trinitrito
A) Triammine trinitrito – N cobalt (III) B) Triammine trinitrito  cobalt (II) C) Triammine cobalt (III) nitrite D) Triammine trinitrito – N cobaltate (III)
cobalt (II) C) Triammine cobalt (III) nitrite D) Triammine trinitrito – N cobaltate (III)
Correct option is A) Triammine trinitrito - N cobalt Triammine trinitro-N-cobalt is the correct IUPAC name (III). In this scenario, the groups are ordered alphabetically, with the ammine group...
Electronic configuration of only one P block element is exceptional. One molecule of that element consists of how many atoms of it ? A) One B) Two C) Three D) Four
The best option is A Explanation: An only p-block element's electrical arrangement is uncommon. There is only one atom of that element in each molecule. Because helium has the electrical...
Which of the following is the most stable diazonium salt ? A) 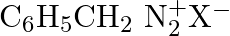 B)
B) 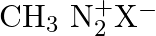 C)
C) 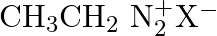 D)
D) 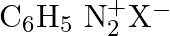
Correct option is B Due to resonance stabilisation between the benzene nucleus and the nitrogen atom, dizonium salts with an aryl group immediately connected to the nitrogen atom are the most...
Which polymer among the following polymers does NOT soften on heating ? A) Bakelite B) Polythene C) Polystyrene D) PVC
The correct option is A Explanation: Thermoplastic is a plastic material that can be melted and moulded repeatedly by just heating it. When heated, thermoplastics soften and become moldable. They...
The relationship between rate constant and half life period of zero order reaction is given by A) ![Rendered by QuickLaTeX.com \mathrm{t}_{\frac{1}{2}}=[\mathrm{A}]_{0} 2 \mathrm{k}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4790aa54d3511e4a28ff21e7043d219a_l3.png) B)
B) 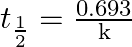 C)
C) ![Rendered by QuickLaTeX.com t_{\frac{1}{2}}=\frac{[\mathrm{A}]_{0}}{2 \mathrm{k}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3dde05612d23f52ee0597c3f471cfe53_l3.png) D)
D) ![Rendered by QuickLaTeX.com \mathrm{t}_{\frac{1}{2}}=\frac{2[\mathrm{~A}]_{0}}{\mathrm{k}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a9a16937140e0a1a6dbc47fd5be5c9a5_l3.png)
Correct option is C $\mathrm{t}_{1 / 2}=\frac{\left[\mathrm{A}_{0}\right]}{2 \mathrm{k}}$ The relationship between rate constant and half-life period of zero-order reaction is given by: $...
Identify a ‘Chemical twin’ among the followings. A) Zr-Ta B) Nb-Tc C) Hf-Re D) Nb-Ta
D is the correct answer. Nb−Ta Chemical twins are those in which some elements' characteristics are identical. Zr and Hf have comparable atomic sizes, as do Nb and Ta. This is related to the...
Chlorination of ethane is carried out in presence of A) anhydrous AlBr3 B) mercuric chloride C) ultraviolet light D) zinc chloride
Correct option is C) ultraviolet light Chlorination of ethane is carried out in the presence of Ultraviolet light to form 1,2-hexachloro ethane.
Which among the following is a tranquilizer ? A) Aspirin B) Valium C) Penicillin D) Sulphanilamide
Correct option is B) Valium A tranquillizer is a medicine that causes people and animals to become calm. Anxiety disorders, alcohol withdrawal symptoms, and muscular spasms are all treated with...
Which among the following alloys is used in making instruments for electrical measurements ? A) Stainless steel B) Manganin C) Spiegeleisen D) Duralumin
Correct option is B) Manganin Manganin foil and wire are employed in the production of resistors, notably ammeter shunts, due to its low temperature coefficient of resistance and long-term...
What is the amount of work done when two moles of ideal gas is compressed from a volume of 1 m3 to 10 dm3 at 300 K against a pressure of 100 kPa ? A) 99 kJ B) – 99 kJ C) 114.9 kJ D) – 114.9 kJ
Correct option is A $99 \mathrm{~kJ}$ $ \mathrm{V}_{1}=1 \mathrm{~m}^{3} $ Pressure $=100 \mathrm{kPa}=100000 \mathrm{~Pa}$ $\mathrm{V}_{2}=10 \mathrm{dm}^{3}=(1 / 100) \mathrm{m}^{3}$ So, $W=P...
What is the possible number of monohydroxy derivatives of a hydrocarbon consisting of five carbon atoms with one methyl group as a branch ? A) 2 B) 3 C) 4 D) 5
Correct option is B Only three isomers of mono hydroxy derivatives of a hydrocarbon with five carbon atoms and one methyl group as a branch are feasible.
Molarity is defined as A) the number of moles of solute dissolved in one dm3 of the solution B) the number of moles of solute dissolved in 1 kg of solvent C) the number of moles of solute dissolved in 1 dm3 of the solvent D) the number of moles of solute dissolved in 100 ml of the solvent
Correct option is (A) The number of moles of solute dissolved in 1dm3 of the solution is called molarity. Molarity = (moles of solute dissoved) / (volume of solvent in dm3) So, answer is...
Which among the following is a feature of adiabatic expansion ? A) ΔV < 0 B) ΔU < 0 C) ΔU > 0 D) ΔT = 0
Correct option is D) ΔT = 0 T=0 for adiabatic expansion. An ideal gas is enclosed in an insulated container and then allowed to expand in a vacuum for adiabatic free expansion. The work done by or...
Half life period of a first order reaction, A→ product is 6.93 hour. What is the value of rate constant ? A) 1.596 h–1 B) 0.1 h–1 C) 4.802 h–1 D) 10 h–1
Correct option is B ($0.1 \mathrm{~h}^{-1}$) We know, $ \mathrm{t}_{\frac{1}{2}}=\frac{0.693}{\mathrm{k}} $ where $t_{\frac{1}{2}}$ is the half life and $\mathrm{k}$ is rate constant. $...
During conversion of glucose into glucose cyanohydrin, what functional group/atom of glucose is replaced ? A) hydrogen B) aldehydic group C) primary alcoholic group D) secondary alcoholic group
Correct option is B Aldehydic group Glucose reacts with hydrogen cyanide to form glucose cyanohydrin. In this reaction functional group is replaced that is −CHO group.
Reaction of which among the following ethers with HI in cold leads to formation of methyl alcohol ? A) ethyl methyl ether B) methyl propyl ether C) isopropyl methyl ether D) tert-butyl methyl ether
Correct option is D) tert-butyl methyl ether
Which among the following detergents is non-ionic in character ? A) Sodiumlauryl sulphate B) Pentaerythrityl stearate C) Cetyltrimethyl ammonium chloride D) Sodium n-dodecyl benzene sulphonate
B is the correct answer. Pentaerythrityl stearate is a kind of stearic acid. The uncharged, hydrophilic headgroups of non-ionic detergents distinguish them from ionic detergents. Polyoxyethylene or...
What oxoacid of sulphur contains S-S bond in its structure ? A) Disulphurous acid B) Disulphuric acid C) Perdisulphuric acid D) Hydrosulphurous acid
Correct option is (A)Disulphurous acid Disulphurous acid(H2S2O5) contain S-S bond in its structure.
A binary operation  on the set
on the set 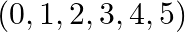 is defined as
is defined as ![Rendered by QuickLaTeX.com \[a * b=\left\{\begin{array}{ll} a+b ; & \text { if } a+b<6 \\ a+b-6 ; & \text { if } a+b \geq 6 \end{array}\right.\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c98db70d6373f329a8c6803f36eeb4ad_l3.png)
Show that 0 is the identity for this operation and each element a has an inverse 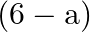 To find: identity and inverse element
To find: identity and inverse element
![Rendered by QuickLaTeX.com \[a * b=\left\{\begin{array}{ll} a+b ; & \text { if } a+b<6 \\ a+b-6 ; & \text { if } a+b \geq 6 \end{array}\right.\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c98db70d6373f329a8c6803f36eeb4ad_l3.png)
For a binary operation if a*e = a, then e s called the right identity If $\mathrm{e}^{*} \mathrm{a}=\mathrm{a}$ then $\mathrm{e}$ is called the left identity For the given binary operation,...
For all 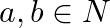 , we define
, we define 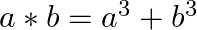 Show that
Show that  is commutative but not associative.
is commutative but not associative.
$\text { let } a=1, b=2 \in N$ $a * b=1^{3}+2^{3}=9$ And $b^{*} a=2^{3}+1^{3}=9$ => ${ }^{*}$ is commutative. Let $c=3$ $\begin{array}{l} (a * b)^{*} c=9 * c=9^{3}+3^{3} \\ a *(b * c)=a...
Show that  on
on 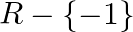 , defined by
, defined by 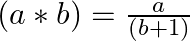 is neither commutative nor associative.
is neither commutative nor associative.
let $\mathrm{a}=1, \mathrm{~b}=0 \in \mathrm{R}-\{-1\}$ $a * b=\frac{1}{0+1}=1$ And $b * a=\frac{0}{1+1}=0$ => $^{*}$ is not commutative. Let $c=3$ $\begin{array}{l} (a * b) * c=1^{*}...
Let 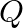 be the set of all positive rational numbers. (iii) Show that * is not associative.
be the set of all positive rational numbers. (iii) Show that * is not associative.
(iii) let $c=3$. $(a * h) * c=1.5 *^{*} c=\frac{1}{-}(15+2)=275$ $a *(b * c)=a * \frac{1}{2}(2+3)=1 * 2.5=\frac{1}{2}(1+2.5)=1.75$ hence * is not associative.
Let 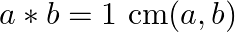 for all values ofa,
for all values ofa, 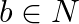 (iii) Find the identity element in N. (iv) Find all invertible elements in
(iii) Find the identity element in N. (iv) Find all invertible elements in 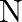 .
.
(iii)let $\mathrm{x} \in \mathrm{N}$ and $\mathrm{x} * 1=\operatorname{lcm}(x, 1)=\mathrm{x}=\operatorname{lcm}(1, \mathrm{x})$ 1 is the identity element. (iv) let there exist $y$ in $n$ such that...
Let  be a binary operation on
be a binary operation on 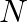 , defined by
, defined by 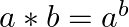 for all a.
for all a. 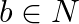 . Show that * is neither commutative nor associative.
. Show that * is neither commutative nor associative.
To prove: $*$ is neither commutative nor associative Let us assume that * is commutative $\Rightarrow a^{b}=b^{a}$ for all $a, b \in N$ This is valid only for $a=b$ For example take $a=1, b=2$...
Show that  on
on 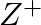 defined by
defined by 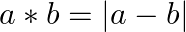 is not a binary operation.
is not a binary operation.
To prove: $*$ is not a binary operation Since, a and $b$ are defined on positive integer set And $\mathrm{a}^{*} \mathrm{~b}=|\mathrm{a}-\mathrm{b}|$ $\Rightarrow a^{*} b=(a-b)$, when $a>b$...
If * be the binary operation on the set 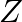 of all integers defined by a
of all integers defined by a 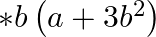 , find
, find 
$2 * 4$ since, $a^{*} b=a+3 b^{2}$ $\Rightarrow 2 * 4=\left(2+3 \times 4^{2}\right)=2+48=50$
Let be a binary operation on the set 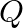 of all rational numbers given as
of all rational numbers given as 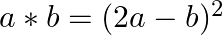 for all
for all 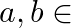 Q. Find
Q. Find  and
and  Is
Is 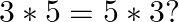
$3 * 5$ and $5 * 3$ $a * b=(2 a-b)^{2}$ $\Rightarrow 3 * 5=(6-5)^{2}=1$ $5 * 3=(10-3)^{2}=49$ $\Rightarrow 3 * 5$ is not equal to $5 * 3$
Let * be a binary operation on the set of all nonzero real numbers, defined by 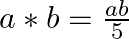 . Find the value of
. Find the value of  given that
given that 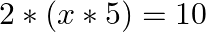
To find: value of $x$ Since, $a * b=\frac{a b}{5}$ $\Rightarrow \mathrm{x} * 5=\frac{5 \mathrm{x}}{5}=\mathrm{x}$ Now $(2 * x)=\frac{2 x}{5}$ $\Rightarrow \frac{2 \mathrm{x}}{5}=10 \Rightarrow...
Let  be a binary operation on the set
be a binary operation on the set  of all integers, defined by a
of all integers, defined by a 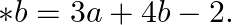 Find the value of
Find the value of 
$4 * 5$ $a * b=3 a+4 b-2$ Since, $a=4$ and $b=5$ $\begin{array}{l} \Rightarrow 4 * 5=3 \times 4+4 \times 5-2=12+20-2=30 \\ \Rightarrow 4 * 5=30 \end{array}$
Evaluate 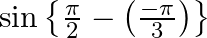
$\begin{array}{l} \sin \left(\frac{\pi}{2}+\frac{\pi}{3}\right) \\ =\sin \left(\frac{5 \pi}{6}\right) \\ =\sin \left(\pi-\frac{\pi}{6}\right) \\ =\sin \frac{\pi}{6} \\ =\frac{1}{2} \end{array}$
Evaluate 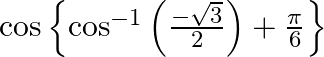
$\cos \left\{\pi-\frac{\pi}{6}+\frac{\pi}{6}\right\}$ $\begin{array}{l} =\cos \{\pi\} \\ =\cos \left(\frac{\pi}{2}+\frac{\pi}{2}\right) \\ =-1 \end{array}$
Find the principal value of : (iii) 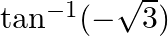 (iv)
(iv) 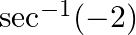
(iii) Let $\tan ^{-1}(-\sqrt{3})=x$ $\Rightarrow-\tan ^{-1}(\sqrt{3})=x\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $\Rightarrow \sqrt{3}=-\tan x$ $\therefore...
Find the principal value of : (vii) 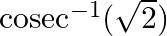
(vii) Let $\operatorname{cosec}^{-1}(\sqrt{2})=x$ $\Rightarrow \sqrt{2}=\operatorname{cosec} x$ $\therefore \mathrm{x}=\frac{\pi}{4}$
Find the principal value of : (v) 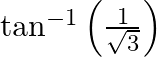 (vi)
(vi) 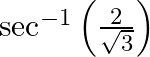
(v) Let $\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=x$ $\Rightarrow \frac{1}{\sqrt{3}}=\tan \mathrm{x}$ [We know which value of $\mathrm{x}$ $\therefore \mathrm{x}=\frac{\pi}{6}$ (vi) Let $\sec...
Find the principal value of : (iii) 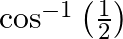 (iv)
(iv) 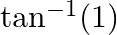
(iii) Let $\cos ^{-1}\left(\frac{1}{2}\right)=x$ $\Rightarrow \frac{1}{2}=\cos x$ [We know which value of $x$ when put in this expression will give us this result] $\therefore...
Find the principal value of : (i) 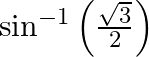 (ii)
(ii) 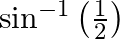
(i) Let $\sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)=x$ $\Rightarrow \frac{\sqrt{3}}{2}=\sin x$ => $\therefore \mathrm{x}=\frac{\pi}{3}$ (ii) Let $\sin ^{-1}\left(\frac{1}{2}\right)=x$ $\Rightarrow...
Given sin-1 (2a/ 1+ a2) + sin-1 (2b/ 1+ b2) = 2 tan-1 x
Prove that: (i) 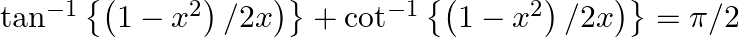 (ii)
(ii) 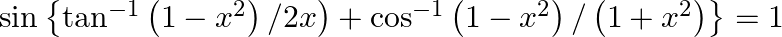
$(i)$ $(ii)$
Prove the following results: (ix) 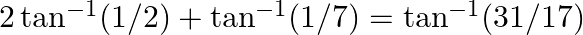 (x)
(x) 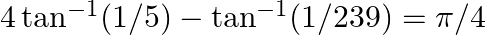
$(ix)$ $(x)$
The 5th term of an AP is 20 and the sum of its 7th and 11th terms is 64. The common difference of the AP is
(a) 4 (b) 5 (c) 3 (d) 2 Answer: (c) 3 We have: a5 = 20 and a7 + a11 = 64. Let a be the first term and d be the common difference of the AP. Then, Thus, the common difference of the AP is...
Prove the following results: (vii) 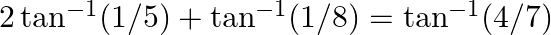 (viii)
(viii) 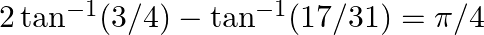
$(vii)$ $(viii)$
Prove the following results: (v) 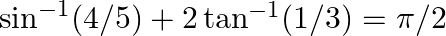 (vi)
(vi) 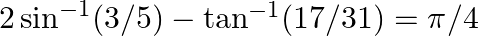
$(v)$ $(vi)$
Prove the following results: (iii) 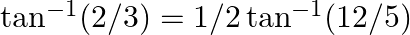 (iv)
(iv) 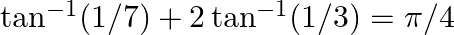
$(iii)$ $(iv)$
Prove the following results: (i) 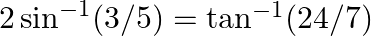 (ii)
(ii) 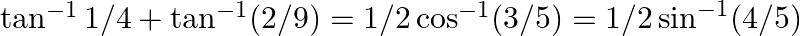
$(i)$ $(ii)$
Evaluate the following: (iii) 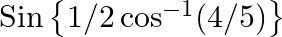 (iv)
(iv) 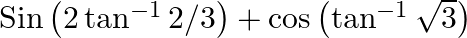
$(iii)$ $(iv)$
The 5th term of an AP is -3 and its common difference is -4. The sum of the first 10 terms is
(a) 50 (b) -50 (c) 30 (d) -30 Answer: (b) -50
Evaluate the following: (i) 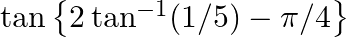 (ii)
(ii) 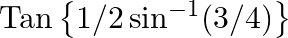
$(i)$ $(ii)$
The 7th term of an AP is -1 and its 16th term is 17. The nth term of the AP is
(a) (3n + 8) (b) (4n – 7) (c) (15 – 2n) (d) (2n – 15) Answer: (d) (2n – 15)
Since, cos-1 (a/x) – cos-1 (b/x) = cos-1 (1/b) – cos-1 (1/a)
The sum of the first n terms of an AP is 4n2 + 2n.The nth term of this AP is
(a) (6n - 2) (b) (7n – 3) (c) (8n – 2) (d) (8n + 2) Answer: (c) (8n – 2)
Given Cos (sin -1 3/5 + sin-1 5/13)
The sum of first n terms of an AP is (5n-n2) The nth term of the AP is
(a) ( 5 - 2n) (b) ( 6 – 2n) (c) (2n – 5) (d) (2n – 6) Answer: (b) ( 6 – 2n)
The sum of the first n terms of an AP is (3n + 6n). The common difference of the AP is
(a) 6 (b) 9 (c) 15 (d) -3 Solution: (a) b
Prove the following results: (iii) 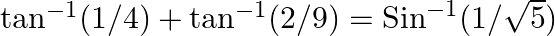
$(iii)$
If the nth term of an AP is (2n + 1) then the sum of its first three terms is
(a) 6n+3 (b) 15 (c) 12 (d) 21 Solution: (b) 15
Prove the following results: (i) 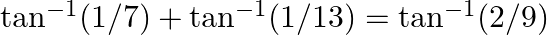 (ii)
(ii) 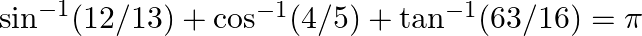
$(i)$ $(ii)$ LHS
If 4, x1,x2, x3, 28 are in AP then x3 =?
(a) 19 (b) 23 (c) 22 (d) cannot be determined Solution: (c) 22
If 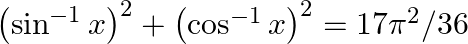 , find
, find 
Since, $\cos ^{-1} x+\sin ^{-1} x=\pi / 2$ => $\cos ^{-1} x=\pi / 2-\sin ^{-1} x$ Substituting this in $\left(\sin ^{-1} x\right)^{2}+\left(\cos ^{-1} x\right)^{2}=17 \pi^{2} / 36$ $\left(\sin...
The next term of the AP 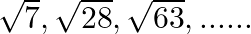 is
is
$ (a)\,\sqrt{84} $ $ (b)\,\sqrt{98} $ $ (c)\,\sqrt{70} $ $ (d)\,\sqrt{112} $ Solution: $ (d)\,\sqrt{112} $ The AP is $ \sqrt{7},\sqrt{28},\sqrt{63},...... $ $ =\sqrt{7},\sqrt{4\times...
$\cot \left(\cos ^{-1} 3 / 5+\sin ^{-1} x\right)=0$ => $\begin{array}{l} \left(\cos ^{-1} 3 / 5+\sin ^{-1} x\right)=\cot ^{-1}(0) \\ \left(\operatorname{Cos}^{-1} 3 / 5+\sin ^{-1} x\right)=\pi /...
Given sin-1 x + sin-1 y = π/3 ……. (i) And cos-1 x – cos-1 y = π/6 ……… (ii)
Since, cos-1 x + cos-1 y = π/4
Evaluate: (v) 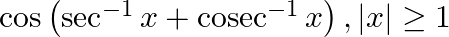
$(v)$ $=>0$
The common difference of the following AP is
(a)1/3 (b)-1/3 (c) b (d) –b Solution: (d) -b
Evaluate: (iii) 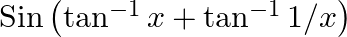 for
for 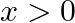 (iv) Cot
(iv) Cot 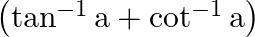
$(iii)$ $(iv)$
Evaluate: (i) 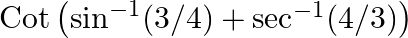 (ii)
(ii) 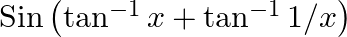 for
for 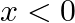
$(i)$ $(ii)$
The common difference of the following AP is
(a) p (b) –p (c) -1 (d) 1 Solution: (c) -1
Evaluate: (iii) cot 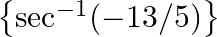
$(iii)$
Evaluate: (i) 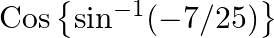 (ii) Sec
(ii) Sec 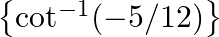
$(i)$ $(ii)$
Evaluate each of the following: (ix) 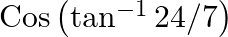
$(ix)$ .
Evaluate each of the following: (vii) Tan 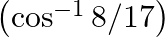 (viii)
(viii) 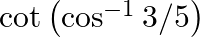
$(vii)$ $(viii)$
Evaluate each of the following: (v) 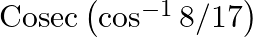 (vi)
(vi) 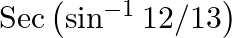
(v) \[\begin{array}{*{35}{l}} {} \\ Let\text{ }co{{s}^{-1}}\left( 8/17 \right)\text{ }=\text{ }y \\ cos\text{ }y\text{ }=\text{ }8/17\text{ }where\text{ }y\text{ }\in \text{ }\left[ 0,\text{ }\pi...
Evaluate each of the following: (iii) 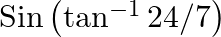 (iv)
(iv) 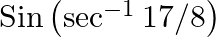
(iii) (iv)
Evaluate each of the following: (i) 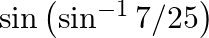 (ii)
(ii) 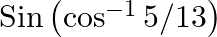
(i) \[\begin{array}{*{35}{l}} Given\text{ }sin\text{ }\left( si{{n}^{-1}}~7/25 \right) \\ let\text{ }y\text{ }=\text{ }si{{n}^{-1}}~7/25 \\ sin\text{ }y\text{ }=\text{ }7/25\text{ }where\text{...
Find the derivative of the function f defined by f (x) = mx + c at x = 0.
f(x) = mx + c, Checking the differentiability at x = 0 This is the derivative of a function at x = 0, and also this is the derivative of this function at every value of x.
If f (x) =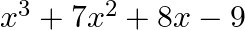 , find f’ (4).
, find f’ (4).
f(x) = x3 + 7x2 + 8x – 9, => Checking the differentiability at x = 4
If for the function Ø (x) =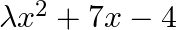 , Ø’ (5) = 97, find λ.
, Ø’ (5) = 97, find λ.
Finding the value of λ given in the real function and we are given with the differentiability of the function f(x) = λx2 + 7x – 4 at x = 5 which is f ‘(5) = 97 =>
Show that the derivative of the function f is given by f (x) = ![Rendered by QuickLaTeX.com \[~\mathbf{2}{{\mathbf{x}}^{\mathbf{3}}}~\text{ }\mathbf{9}{{\mathbf{x}}^{\mathbf{2}~}}+\text{ }\mathbf{12}\text{ }\mathbf{x}\text{ }+\text{ }\mathbf{9}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c388eec2224700cda456bd12406ee5c9_l3.png)
, at x = 1 and x = 2 are equal.
We are given with a polynomial function f(x) = 2x3 – 9x2 + 12x + 9, and we have
If f is defined by f (x) = 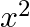 – 4x + 7, show that f’ (5) = 2 f’ (7/2)
– 4x + 7, show that f’ (5) = 2 f’ (7/2)
Discuss the continuity and differentiability of the function f (x) = |x| + |x -1| in the interval of (-1, 2).
Since, a polynomial and a constant function is continuous and differentiable everywhere => f(x) is continuous and differentiable for x ∈ (-1, 0) and x ∈ (0, 1) and (1, 2). Checking continuity...
Show that the function  is defined as follows
is defined as follows 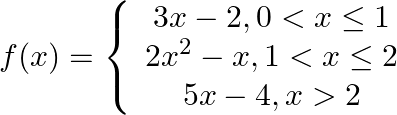 Is continuous at
Is continuous at 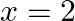 , but not differentiable thereat.
, but not differentiable thereat.
Since, LHL = RHL = f (2) Hence, F(x) is continuous at x = 2 Checking the differentiability at x = 2 $=> 5$ Since, (RHD at x = 2) ≠ (LHD at x = 2) Hence, f (2) is not differentiable at x =...
checking differentiability of given function at x = 3 => LHD (at x = 3) = RHD (at x = 3) = 12 Since, (LHD at x = 3) = (RHD at x = 3) Hence, f(x) is differentiable at x = 3.
Show that f (x) =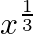 is not differentiable at x = 0.
is not differentiable at x = 0.
Since, LHD and RHD does not exist at x = 0 Hence, f(x) is not differentiable at x = 0
Show that f (x) = |x – 3| is continuous but not differentiable at x = 3.
In potentiometer experiment, the potential gradient can be increased by
A. increasing the cross-sectional area of the potentiometer wire.
B. using a wire of material of low specific resistance.
C. decreasing the cross-sectional area of the potentiometer wire.
D. decreasing the current through it.
Correct answer is C.
When a resistance ‘ 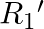 is connected across the terminal of a cell of e.m.f. ‘
is connected across the terminal of a cell of e.m.f. ‘ 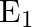 ‘ the current is ‘
‘ the current is ‘ 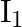 ‘. When the resistance is changed to
‘. When the resistance is changed to 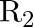 ‘ the current is ‘
‘ the current is ‘ 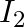 ‘. The internal resistance of the cell is
‘. The internal resistance of the cell is
A. 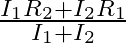
B. 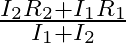
C. 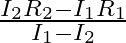
D. 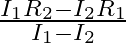
Correct answer is C. $\begin{array}{l} I_{1}=\frac{E}{r+R_{1}} \\ I_{2}=\frac{E}{r+R_{2}} \\ \frac{I_{1}}{I_{2}}=\frac{r+R_{2}}{r+R_{1}} \\ I_{1} r+I_{1} R_{1}=I_{2} r+I_{2} R_{2} \\...
The dimensions of angular momentum are
A. ![Rendered by QuickLaTeX.com \left[L^{2} M^{1} T^{-1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e3ae8151d351e21d072dc99a517680a5_l3.png)
B. ![Rendered by QuickLaTeX.com \left[L^{2} M^{2} T^{-2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-570bf7fd6b73030ec948ef99c8b75448_l3.png)
C. ![Rendered by QuickLaTeX.com \left[L^{2} M^{1} T^{1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8a2e9f8d186a5b9fceddc341575a2dfb_l3.png)
D. ![Rendered by QuickLaTeX.com \left[L^{2} M^{1} T^{-2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6d349a07b4098874e03d0238509c1b23_l3.png)
Correct answer is A.
Work done by the force on the body is the measure of the change in its
A. momentum.
B. mass.
C. potential energy.
D. kinetic energy.
Correct answer is D.
A wire suspended vertically is stretched by 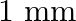 , when mass of
, when mass of 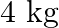 is attached to the lower end. Energy gained by the wire is (Take
is attached to the lower end. Energy gained by the wire is (Take 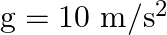 )
)
A. 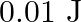
B. 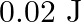
C. 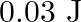
D. 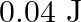
Correct answer is B
Three vessels A, B, C of different shapes have same base area and are filled with water up to same height ‘ 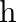 ‘. The respective forces exerted by water on the bases are ‘
‘. The respective forces exerted by water on the bases are ‘  and respective weights are
and respective weights are 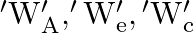 . Then
. Then
A. 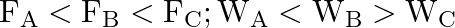
B. 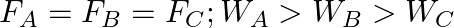
C. 
D. 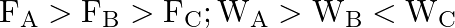
Correct answer is B.
In case of Light Emitting Diode (LED) light is emitted due to A. recombination of holes and electrons.
B. emission of holes and electrons.
C. diffusion of holes.
D. drifting of electrons
Correct answer is A.
The sequence of harmonics of a pipe open at one end and closed at the other end is 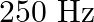 and
and 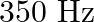 . The resonating length of the air column in its fundamental mode will be (velocity of sound in air
. The resonating length of the air column in its fundamental mode will be (velocity of sound in air 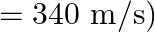
A. 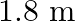
B. 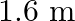
C. 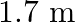
D. 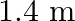
Correct answer is C. $\begin{array}{l} 2 n=n_{2}-n_{1} \\ =350-250=100 \\ n=\frac{100}{2}=50 H z \\ n=\frac{v}{4 l_{0}}=\frac{340}{4 \times l_{0}} \\ \therefore l=\frac{340}{4 \times...
The ratio of magnetization and magnetic intensity is called
A. permeability
B. magnetic induction
C. magnetic susceptibility
D. gyromagnetic ratio
Correct answer is C.
The ratio of magnetic induction along the axis to magnetic induction along the equator of a bar magnet for a point at the same distance 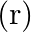 from the centre of magnet is
from the centre of magnet is
A. 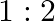
B. 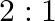
C. 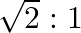
D. 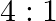
Correct answer is B. Magnetic induction at axial point $=\overrightarrow{\mathrm{B}}$ axial $=\frac{\mu \circ}{4 \pi} \frac{2 \overrightarrow{\mathrm{m}}}{\mathrm{r}^{3}}$ Magnetic induction at...
A metal surface ejects electrons when irradiated by blue light, but not when irradiated by green light. The electrons will also be ejected by the surface, when irradiated by
A. red light
B. voilet light
C. orange light
D. yellow light
Correct answer is B.
Two long, straight wires are set parallel to each other. Both the wires carry a current ‘I’ in opposite directions and separation between them is ‘ 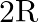 ‘. The magnetic induction at the midway between them is
‘. The magnetic induction at the midway between them is 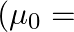 permeability of free space)
permeability of free space)
A. Zero
B. 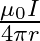
C. 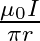
D. 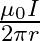
Correct answer is A. $\begin{array}{l} \mathrm{x}=\frac{\mathrm{r}}{2} \\ \mathrm{~B}_{1}=-\frac{\mu_{0} \mathrm{i}}{2 \pi \mathrm{x}} \\ \mathrm{B}_{2}=\frac{\mu_{0} \mathrm{i}}{2...
The component of the vector 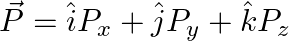 along the direction of
along the direction of 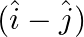 is
is
A. 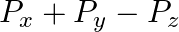
B. 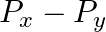
C. 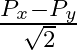
D. 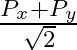
Correct answer is C.
A charged capacitor has charge ‘ 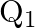 ‘ at potential
‘ at potential 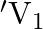 ‘. The charge on capacitor is increased to ‘
‘. The charge on capacitor is increased to ‘ 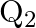 ‘ so that its potential increases to
‘ so that its potential increases to 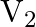 , then the difference between final and initial energy stored in capacitor is
, then the difference between final and initial energy stored in capacitor is
A. 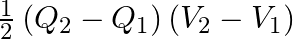
B. 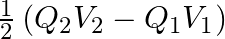
C. 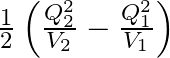
D. 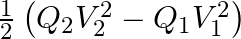
Correct answer is B.
In the formula for high resolving power microscope, the numerical aperture of the object of the microscope is given as 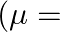 refractive index of oil and angle made by the object at the aperture =
refractive index of oil and angle made by the object at the aperture = 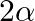 )
)
A. 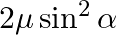
B. 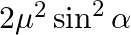
C. 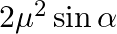
D. 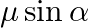
Correct answer is D.
Bending of beam can be reduced by using
A. a material with large value of Young’s modulus.
B. small value of the depth of the bar
C. large value of the length of the beam.
D. small value of the breadth of the bar
Correct answer is A.
‘M’ 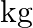 weight is suspended from a weightless spring and it has period ‘
weight is suspended from a weightless spring and it has period ‘ 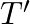 . If now ‘
. If now ‘ 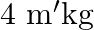 weight is suspended from the same spring, the new period will be
weight is suspended from the same spring, the new period will be
A. 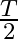
B. 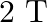
C. 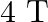
D. 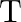
Correct answer is B. $\begin{array}{l} \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}} \\ \mathrm{T}_{1}=\mathrm{T} \\ \mathrm{m}_{1}=1 \mathrm{~kg} \\ \mathrm{~m}_{2}=4 \mathrm{~kg} \\...
A conical pendulum has bob of mass of 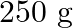 and a length of
and a length of 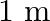 . If the horizontal circle traced by the bob has a diameter of
. If the horizontal circle traced by the bob has a diameter of  , then the tension in the string would be nearly
, then the tension in the string would be nearly 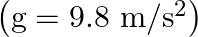
A. 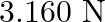
B. 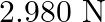
C. 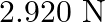
D. 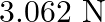
Correct answer is D.
In Biprism experiment the distance between the two virtual images of the slits in the magnified and diminished position are 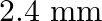 and
and 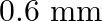 respectively. The distance between two coherent sources is
respectively. The distance between two coherent sources is
A. 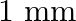
B. 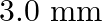
C. 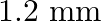
D. 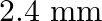
Correct answer is C. When, 1) magnified, distance between images, $\mathrm{d}_{1}=2.4$ 2) dimnished, distance between images, $\mathrm{d}_{2}=0.6$ $\therefore$ Distance between virtual sources...
Half-lives of two radioactive elements A and B are 20 minute and 40 minute respectively. Initially the samples have equal nuclei. After 80 minute, the ratio of decayed number of A and B nuclei will be
A. 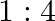
B. 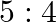
C. 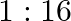
D. 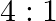
Correct answer is B. $\begin{array}{l} \mathrm{n}=\mathrm{n}_{0} \mathrm{e}^{-\alpha t} \\ \alpha_{\mathrm{A}}=\ln 2 / 20 \\ \alpha_{\mathrm{B}}=\ln 2 / 40 \end{array}$ After 80 min, remaining...
The S.I. unit of impulse is the same as that of
A. linear velocity.
B. angular velocity.
C. linear momentum.
D. angular momentum.
Correct answer is C.
Dimensions of magnetic intensity are
A. ![Rendered by QuickLaTeX.com \left[L^{-1} M^{0} T^{0} I^{1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-61bc00b014420d451f210b1b6d369577_l3.png)
B. ![Rendered by QuickLaTeX.com \left[L^{-1} M^{0} T^{0} I^{-1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c460b6b0a8d363b4b9c32706e423f306_l3.png)
C. ![Rendered by QuickLaTeX.com \left[L^{-1} M^{0} T^{0} I^{-1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c460b6b0a8d363b4b9c32706e423f306_l3.png)
D. ![Rendered by QuickLaTeX.com \left[L^{-1} M^{1} T^{1} I^{-1}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9ab8d27e17f1706b0fe994dd5197b794_l3.png)
Correct answer is A.
Two vibrating tuning forks produce waves which are represented by 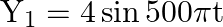 and
and 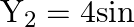
 . The number of beats produced per minute by these two waves is
. The number of beats produced per minute by these two waves is
A. 60
B. 180
C. 360
D. 3
Correct answer is B. $\begin{array}{l} \mathrm{Y}_{1}=4 \sin (500 \pi \mathrm{t}) \\ \mathrm{Y}_{2}=2 \sin (506 \pi \mathrm{t}) \\ \mathrm{f}_{1}=\frac{\omega_{1}}{2 \pi}=\frac{500 \pi}{2 \pi}=250...
The innermost orbit of the hydrogen atom has a diameter of 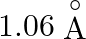 , the diameter of the tenth orbit is
, the diameter of the tenth orbit is
A. 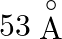
B. 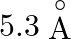
C. 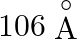
D. 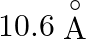
Correct answer is C. Radius of an atom is directly proportional to $n^{2}$ and radius of $n$th orbit which is equal to radius of first orbit multiplied by $n^{2}$ So that will give you. Diameter of...
A sonometer wire of length ‘ 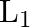 ‘ is in unison with a tuning fork of frequency’n’. When the vibrating length of the wire is reduced to ‘
‘ is in unison with a tuning fork of frequency’n’. When the vibrating length of the wire is reduced to ‘ 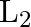 ‘, it produces ‘
‘, it produces ‘ 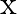 ‘ beats per second with the fork. The frequency of the fork is
‘ beats per second with the fork. The frequency of the fork is
A. 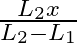
B. 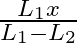
C. 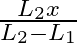
D. 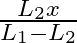
Correct answer is D. For the length $L_{1}, n_{1}=\frac{1}{2 L_{1}} \sqrt{\frac{T}{m}}=n \ldots(1)$ where $m=$ mass per unit length For the length $L_{2}, n_{2}=\frac{1}{2 L_{2}} \sqrt{\frac{T}{m}}...
Which of the following statements is NOT true for a particle moving in circle with a constant angular speed?
A. The radial acceleration vector is tangent to the circle.
B. The linear velocity vector is tangent to the circle.
C. The radial acceleration vector points towards the centre of the circle.
D. The linear velocity and radial acceleration vectors at a point are perpendicular to each other.
Correct answer is A.
A particle performs simple harmonic motion from mean position, with period 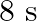 . The distance travelled by it between 1 st and 2 nd second of its motion is (A = amplitude of S. H. M.)
. The distance travelled by it between 1 st and 2 nd second of its motion is (A = amplitude of S. H. M.)
A. 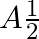
B. 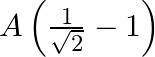
C. 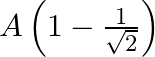
D. 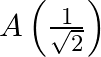
Correct answer is C. In $2 \mathrm{~s}$ (which is equal to $\frac{T}{4}$ ), one amplitude will be convered. In $1 \mathrm{st}$ second $x=a \sin \left(\frac{\pi}{4}\right)=\frac{a}{\sqrt{2}}$...
A capillary tube is dipped in water, the water rises in it to a height ‘h’. If ‘ 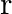 ‘ is the radius of bore of tube then
‘ is the radius of bore of tube then
A. 
B. 
C. 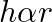
D. 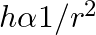
Correct answer is B. We have, $\mathrm{h}=\frac{2 \sigma \cos \theta}{\mathrm{r} \rho \mathrm{g}}$ $\Rightarrow \mathrm{h} \cdot \mathrm{r}=$ constant
When an npn transistor is used as an amplifier
A. electrons move from base to collector.
B. holes move from emitter to base.
C. electrons move from collector to base,
D. holes move from base to collector.
Correct answer is A.
A charge ‘ 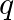 ‘ is enclosed by a Gaussian spherical surface of radius ‘R’. If, now, radius of the spherical surface is doubled the outward electric flux will
‘ is enclosed by a Gaussian spherical surface of radius ‘R’. If, now, radius of the spherical surface is doubled the outward electric flux will
A. doubled
B. remain same
C. increase four times
D. reduce to half
Correct answer is B. Method 1: Using Number of Field Lines - We know that, Electric flux is proportional to number of field lines. - Form figure, we see that the number of field lines crossing both...
The rate of cooling of a body is 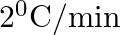 when the body is at
when the body is at 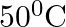 above the temperature of surroundings. When the body is at
above the temperature of surroundings. When the body is at 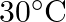 above the temperature of surroundings, its rate of cooling will be
above the temperature of surroundings, its rate of cooling will be
A. 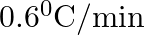
B. 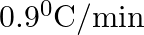
C. 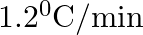
D. 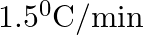
Correct answer is C. Rate of cooling $\frac{\mathrm{dT}}{\mathrm{dt}}=-\frac{\mathrm{k}}{\mathrm{ms}}\left(\mathrm{T}-\mathrm{T}_{\mathrm{s}}\right)$ Or $2=\frac{-\mathrm{k}}{\mathrm{ms}}(50)$ Or...

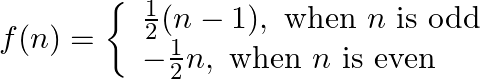 is both one – one and onto.
is both one – one and onto.