Gravitation Archives - Noon Academy

Gravitation

A satellite is in an elliptic orbit around the earth with an aphelion of 6R and perihelion of 2R where R = 6400 km is the radius of the earth. Find eccentrically of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Solution: Radius of perigee is given as $r_{p}=2R$ Radius of apogee is given as $r_{a}=6R$ And we know, $r_{p}=a(1-e)=2R$ and, $r_{a}=a(1+e)=6R$ From the above equations, we get $e = 1/2$ From the...

Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, the earth’s distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant throughout the year. Assume that earth’s spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain the variation of the length of the day during the year?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Solution: Velocity of the earth at perigee is given as $v_{p}$ Velocity of the earth at apogee is given as $v_{a}$ Angular velocity of the earth at perihelion is given as $\omega_{p}$ Angular...

A satellite is to be placed in equatorial geostationary orbit around the earth for communication
a) calculate height of such a satellite
b) find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

a) Mass of the earth is given as $M=6\times 10^{24}kg$ Radius of the earth is given as $R=6.4 \times 10^{3}m$ Time period is given as $24.36 \times 10^{2}s$ $G=6.67 \times 10^{-11}Nm^{2}kg^{-1}$...

Six-point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

$AE = AG + EG$ $AG + AG = 2AG$ $= 2l cos 30^{o}$ $AE = AC = \sqrt3l$ $AD = 2l$ As a result, $\frac{Gm^{2}}{l^{2}}$ is the force on A due to B along B to A $\frac{Gm^{2}}{3l^{2}}$ is the force on A...

A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E, and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

When a body moves around a star in equilibrium, the gravitational attraction produces a centripetal force. Consider a body of mass $m$ revolving in a circular path of radius $r$ around the star S of...

A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r. If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h = r?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Solution: Let the radius of the ring be r Let the mass of the ring be m When small element dM is considered as the mass, the gravitation force becomes, $dF=\frac{G(dM)m}{x^{2}}$ where...

An object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Potential Energy of the body on the earth is given by $-GMm/R$ When the body is closer to the equator, then PE becomes $-GMm/2R$ Gain in PE is $1/2 mgR$

Shown are several curves. Explain with reason, which ones amongst them can be possible trajectories traced by a projectile

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Solution: Amongst the given figures, (c) show the focus of trajectory.

Show the nature of the following graph for a satellite orbiting the earth.
TE vs orbital radius R

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Total energy of the satellite is $-GMm/2R$

Show the nature of the following graph for a satellite orbiting the earth.
a) KE vs orbital radius R
b) PE vs orbital radius R

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

a) $\mathrm{K}=1 / 2 \mathrm{mv}^{2}=(1 / 2 \mathrm{~m})(\mathrm{GM} / \mathrm{R})$ b) PE of satellite is $U = -GMm/R = -2K$

Two identical heavy spheres are separated by a distance 10 times their radius. Will an object placed at the midpoint of the line joining their centres be in stable equilibrium or unstable equilibrium? Give a reason for your answer.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

M = mass of the spheres R = radius of the spheres. P = midpoint of A and B. The magnitude of the force is expressed as, $F_{1}=F_{2}=\frac{GMm}{5R^{2}}$ As the resultant force exerted on the object...

Mean solar day is the time interval between two successive noon when the sun passes through zenith point. The sidereal day is the time interval between two successive transits of a distant star through the zenith point. By drawing the appropriate diagram showing earth’s spin and orbital motion, show that mean solar day is four minutes longer than the sidereal day. In other words, distant stars would rise 4 minutes early every successive day.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The polar axis of the earth and its movement are E and E’ respectively. Translational motion is P’ After every 24 hours, earth's orbit is approximately advanced by $1^{o}$ As a result, time taken...

What is the angle between the equatorial plane and the orbital plane of
a) polar satellite?
b) geostationary satellite?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

a) The equatorial plane and the orbital plane of a polar satellite form a $90^{o}$ angle. b) A geostationary satellite's equatorial plane and orbital plane are at an angle of $0^{o}$.

Out of aphelion and perihelion, where is the speed of the earth more and why?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

According to Kepler’s second law, a real velocity is constant and is given as: $r_{p}\times v_{p}=r_{A}\times v_{A}$ $\frac{r_{A}}{r_{p}}=\frac{v_{p}}{v_{A}}$ $r_{A}>r_{p}$ and...

The gravitational force between a hollow spherical shell and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

R is the spherical shell's radius, while r is the distance between m and M. The point's mass is m, while the hollow spherical shell's mass is M. Now, $F=\frac{GMm}{r^{2}}$ When F = 0,...

An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The astronaut will experience variation when the size of the space station orbiting the earth is large, and this is due to acceleration due to gravity.

We can shield a charge from electric fields by putting it side a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

No. As gravitation is independent of the medium, a body can be shielded from the gravitational pull of adjacent matter.

Is it possible for a body to have inertia but no weight?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Yes. It is possible for a body to have inertia but no weight as inertia is associated with the mass of the body. Satellite revolving around the earth is an example of a body with inertia and has no...

How is the gravitational force between two point masses affected when they are dipped in the water keeping the separation between them the same?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The gravitational force between point masses is unaffected by the medium and remains constant regardless of their surroundings. As a result, even if the two-point masses are submerged in water, the...

What is the direction of areal velocity of the earth around the sun?

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The direction of the earth's areal velocity around the sun is determined by the product of r and v.

Give one example each of central force and non-central force.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

Example of Central force: Electrostatic force acting on the point charge Example of Non-central force: Nuclear force between the atoms

Molecules in the air in the atmosphere are attracted by the gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The gravitational force of the earth attracts molecules in the atmosphere, yet they do not descend into the earth since they are in random motion, whereas an apple moves downhill.

The centre of mass of an extended body on the surface of the earth and its centre of gravity
a) are always at the same point for any size of the body
b) are always at the same point only for spherical bodies
c) can never be at the same point
d) is close to each other for objects, say of sizes less than 100 m
e) both can change if the object is taken deep inside the earth

CBSE, Class 11, Gravitation, Physics, Physics

The correct option is d) is close to each other for objects, say of sizes less than 100 m

Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read Exemplar Solutions Physics Class 11 Chapter 8 – 21 where Mo is a constant of the dimension of mass, r12 = r1 – r2 and n is a number. In such a case,
a) the acceleration due to gravity on earth will be different for different object
b) none of the three laws of Kepler will be valid
c) only the third law will become invalid
d) for n negative, an object lighter than water will sink in water

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct options are a) the acceleration due to gravity on earth will be different for different object c) only the third law will become invalid d) for n negative, an object lighter than water...

There have been suggestions that the value of the gravitational constant G becomes smaller when considered over a very large time period in the future. If that happens for our earth,
a) nothing will change
b) we will become hotter after billions of years
c) we will be going around but not strictly in closed orbits
d) after a sufficiently long time we will leave the solar system

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct options are c) we will be going around but not strictly in closed orbits d) after a sufficiently long time we will leave the solar system

If the sun and the planets carried huge amounts of opposite charges,
a) all three of Kepler’s laws would still be valid
b) only the third law will be valid
c) the second law will not change
d) the first law will still be valid

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct options are a) all three of Kepler’s laws would still be valid c) the second law will not change d) the first law will still be valid

If the mass of sun were ten times smaller and gravitational constant G were ten times larger in magnitudes
a) walking on ground would become more difficult
b) the acceleration due to gravity on earth will not change
c) raindrops will fall much faster
d) aeroplanes will have to travel much faster

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct options are a) walking on ground would become more difficult c) raindrops will fall much faster d) aeroplanes will have to travel much faster

If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube-law
a) planets will not have elliptic orbits
b) circular orbits of planets is not possible
c) projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic
d) there will be no gravitational force inside a spherical shell of uniform density

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct options are a) planets will not have elliptic orbits c) projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic Explanation: The planets...

Which of the following options is correct?
a) acceleration due to gravity decreases with increasing altitude
b) acceleration due to gravity increases with increasing depth
c) acceleration due to gravity increases with increasing latitude
d) acceleration due to gravity is independent of the mass of the earth

CBSE, Class 11, Gravitation, Physics, Physics

The correct options are a) acceleration due to gravity decreases with increasing altitude c) acceleration due to gravity increases with increasing latitude

Particles of masses 2M, m and M are respectively at points A, B, and C with AB = 1/2 (BC). M is much-much smaller than M and at time t = 0, they are all at rest. At subsequent times before any collision takes place

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

a) m will remain at rest b) m will move towards M c) m will move towards 2M d) m will have oscillatory motion Solution: The correct option is c) m will move towards 2M

Choose the wrong option.
a) inertial mass is a measure of the difficulty of accelerating a body by an external force whereas the gravitational mass is relevant in determining the gravitational force on it by an external mass
b) that the gravitational mass and inertial mass are equal is an experimental result
c) that the acceleration due to gravity on earth is the same for all bodies is due to the equality of gravitational mass and inertial mass
d) gravitational mass of a particle-like proton can depend on the presence of neighbouring heavy objects but the inertial mass cannot

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is d) gravitational mass of a particle-like proton can depend on the presence of neighbouring heavy objects but the inertial mass cannot

In our solar system, the inter-planetary region has chunks of matter called asteroids. They
a) will not move around the sun since they have very small masses compared to the sun
b) will move in an irregular way because of their small masses and will drift away outer space
c) will move around the sun in closed orbits but not obey Kepler’s laws
d) will move in orbits like planets and obey Kepler’s laws

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is d) will move in orbits like planets and obey Kepler’s laws

Both earth and moon are subject to the gravitational force of the sun. as observed from the sun, the orbit of the moon
a) will be elliptical

will not be strictly elliptical because the total gravitational force on it is not central
c) is not elliptical but will necessarily be a closed curve
d) deviates considerably from being elliptical due to the influence of planets other than earth

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is b) will not be strictly elliptical because the total gravitational force on it is not central

Satellites orbiting the earth have a finite life and sometimes debris of satellites fall to the earth. This is because
a) the solar cells and batteries in satellites run out
b) the laws of gravitation predict a trajectory spiralling inwards
c) of viscous forces causing the speed of the satellite and hence height to gradually decrease
d) of collisions with other satellites

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is c) of viscous forces causing the speed of the satellite and hence height to gradually decrease

Different points in the earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the cm causing translation and a net torque at the cm causing translation and a net torque at the cm causing rotation around an axis through the cm. For the earth-sun system
a) the torque is zero
b) the torque causes the earth to spin
c) the rigid body result is not applicable since the earth is not even approximately a rigid body
d) the torque causes the earth to move around the sun

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is a) the torque is zero

As observed from earth, the sun appears to move in an approximately circular orbit. For the motion of another planet like mercury as observed from earth, this would
a) be similarly true
b) not be true because the force between earth and mercury is not inverse square law
c) not be true because the major gravitational force on mercury is due to sun
d) not be true because mercury is influenced by forces other than gravitational forces

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is c) not be true because the major gravitational force on mercury is due to sun

The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity
a) will be directed towards the centre but not the same everywhere
b) will have the same value everywhere but not directed towards the centre
c) will be same everywhere in magnitude directed towards the centre
d) cannot be zero at any point

CBSE, Class 11, Gravitation, NCERT Exemplar, Physics

The correct option is d) cannot be zero at any point

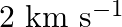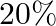A rocket is fired ‘vertically’ from the surface of mars with a speed of $2 \mathrm{~km} \mathrm{~s}^{-1}$ . If $20 \%$ of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it? Mass of mars 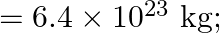$=6.4 \times 10^{23} \mathrm{~kg} ;$ radius of mars 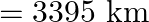$=3395 \mathrm{~km}$ ; G $=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2} .$

CBSE, Class 11, Gravitation, NCERT, Physics

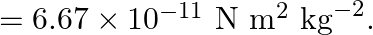
Velocity of the rocket fired from the surface of $\operatorname{mars}(v)=2 \mathrm{~km} / \mathrm{s}$ Let $m$ be the mass of the rocket Mass of the Mars is given as $(M)=6.4 \times 10^{23}...

A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system? Mass of the space ship 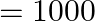$=1000$ kg; mass of the sun = 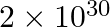$2 \times 10^{30}$ kg; mass of mars 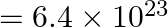$=6.4 \times 10^{23}$ kg; radius of mars 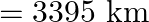$=3395 \mathrm{~km}$ ; radius of the orbit of mars $=$ $2.28 \times 10^{8} \mathrm{~km} ; \mathbf{G}=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2} .$

CBSE, Class 11, Gravitation, NCERT, Physics

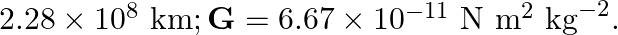
Mass of the spaceship is given as $m_{s}=1000 \mathrm{~kg}$ Mass of the Sun is given as $M=2 \times 10^{30} \mathrm{~kg}$ Mass of Mars is given as $m_{m}=6.4 \times 10^{23} \mathrm{~kg}$ Radius of...

A star 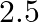$2.5$ times the mass of the sun and collapsed to a size of 12 km rotates with a speed of 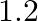$1.2$ rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity? (mass of the sun $=2 \times 10^{30} \mathrm{~kg}$ ).

CBSE, Class 11, Gravitation, NCERT, Physics

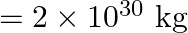If the outward centrifugal force is lesser than the inward gravitational pull, any matter will remain stuck to the surface. Gravitational force is given by the relation: $f_{G}=\frac{G M m}{R^{2}}$...

As you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 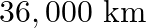$36,000 \mathrm{~km}$ from the surface of the earth. What is the potential due to earth’s gravity at the site of this satellite? (Take the potential energy at infinity to be zero). Mass of the earth = $6.0 \times 10^{24} \mathrm{~kg}$ , radius $=\mathbf{6 4 0 0} \mathrm{km}$ .

CBSE, Class 11, Gravitation, NCERT, Physics

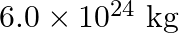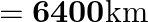Radius of the Earth is given as $R=6400 \mathrm{~km}=0.64 \times 10^{7} \mathrm{~m}$ Mass of Earth is known as $M=6 \times 10^{24} \mathrm{~kg}$ Height of the geostationary satellite from earth's...

Two heavy spheres each of mass 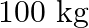$100 \mathrm{~kg}$ and radius 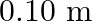$0.10 \mathrm{~m}$ are placed 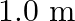$1.0 \mathrm{~m}$ apart on a horizontal table. What is the gravitational force and potential at the midpoint of the line joining the centres of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?

CBSE, Class 11, Gravitation, NCERT, Physics

Radius of spheres is given as $R=0.10 \mathrm{~m}$ Distance between two spheres is given as $r=1.0 \mathrm{~m}$ Mass of each sphere is given as $M=100 \mathrm{~kg}$ We can infer from the figure that...

Two stars each of one solar mass 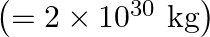$\left(=2 \times 10^{30} \mathrm{~kg}\right)$ are approaching each other for a headon collision. When they are a distance 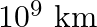$10^{9} \mathrm{~km}$ , their speeds are negligible. What is the speed with which they collide? The radius of each star is 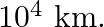$10^{4} \mathrm{~km} .$ Assume the stars to remain undistorted until they collide. (Use the known value of G).

CBSE, Class 11, Gravitation, NCERT, Physics

Mass of each star is given as $M=2 \times 10^{30} \mathrm{~kg}$ Radius of each star is given as $R=10^{4} \mathrm{~km}=10^{7} \mathrm{~m}$ Distance between the stars is given as $r=10^{9}...

A satellite orbits the earth at a height of 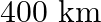$400 \mathrm{~km}$ above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite 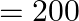$=200$ kg; mass of the earth 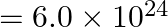$=6.0 \times 10^{24}$ kg; radius of the earth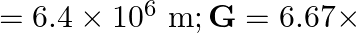 $=6.4 \times 10^{6} \mathrm{~m} ; \mathbf{G}=6.67 \times$ $10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2}$

CBSE, Class 11, Gravitation, NCERT, Physics

Height of the satellite is given as $h=400 \mathrm{~km}=4 \times 10^{5} \mathrm{~m}$ Mass of the Earth is known as $M=6.0 \times 10^{24} \mathrm{~kg}$ Mass of the satellite is given as $m=200...

The escape speed of a projectile on the earth’s surface is 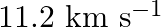$11.2 \mathrm{~km} \mathrm{~s}^{-1}$ . A body is projected out with thrice this speed. What is the speed of the body far away from the earth? Ignore the presence of the sun and other planets.

CBSE, Class 11, Gravitation, NCERT, Physics

Escape velocity of the projectile on the Earth's surface is given as $\mathrm{V}_{\mathrm{e}}=11.2 \mathrm{~km} / \mathrm{s}$ Velocity of projection of the body will be, $v=3 \mathrm{Ve}=3 \times...

A rocket is fired vertically with a speed of 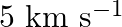$5 \mathrm{~km} \mathrm{~s}^{-1}$ from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth 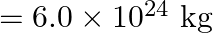$=6.0 \times 10^{24} \mathrm{~kg}$ ; mean radius of the earth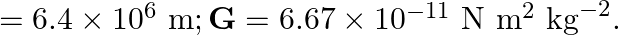 $=6.4 \times 10^{6} \mathrm{~m} ; \mathbf{G}=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2} .$

CBSE, Class 11, Gravitation, NCERT, Physics

Velocity of the missile is given as $v=5 \times 10^{3} \mathrm{~m} / \mathrm{s}$ Mass of the Earth is known as $M_{E}=6 \times 10^{24} \mathrm{~kg}$ Radius of the Earth is given as $R_{E}=6.4 \times...

Assuming the earth to be a sphere of uniform mass density, how much would a body weigh halfway down to the centre of the earth if it weighed 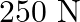$250 \mathrm{~N}$ on the surface?

CBSE, Class 11, Gravitation, NCERT, Physics

Weight of a body on the Earth's surface is given as $W=m g=250 \mathrm{~N}$ Let $R_{e}$ be the radius of the earth Let $d$ be at a distance halfway to the centre of the earth, then, $d=R_{e} / 2$...

A body weighs 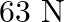$63 \mathrm{~N}$ on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?

CBSE, Class 11, Gravitation, NCERT, Physics

Weight of the man is given as $W=63 \mathrm{~N}$ Acceleration due to gravity at height 'h' from the Earth's surface is: g'=g1+hRe2...

A Saturn year is 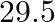$29.5$ times the Earth year. How far is the Saturn from the Sun if the Earth is 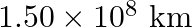$1.50 \times 10^{8} \mathrm{~km}$ away from the Sun?

CBSE, Class 11, Gravitation, NCERT, Physics

According to Kepler's third law of planetary motion, the following relation can be written, $T=\sqrt{\frac{4 \pi^{2} r^{3}}{G M}}$ We get $\mathrm{T}^{2} \propto \mathrm{r}^{3}$ from the above...

How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 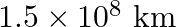$1.5 \times 10^{8} \mathrm{~km}$ .

CBSE, Class 11, Gravitation, NCERT, Physics

Earth's orbit has a radius of $r=1.5 \times 10^{11} \mathrm{~m}$ Time taken by the Earth for one complete revolution can be $\mathrm{T}=1$ year $=365.25$ days i.e. $T=(365.25 \times 24 \times 60...

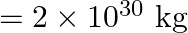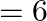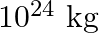A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun $=2 \times 10^{30} \mathrm{~kg}$ , mass of the earth $=6$ x $10^{24} \mathrm{~kg}$ . Neglect the effect of other planets etc. (orbital radius $=1.5 \times 10^{11} \mathrm{~m}$ ).

CBSE, Class 11, Gravitation, NCERT, Physics

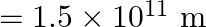Mass of Sun is given as $M_{\text {sun }}=2 \times 10^{30} \mathrm{~kg}$ Mass of Earth is given as $M_{\text {earth }}=6 \times 10^{24} \mathrm{~kg}$ Orbital radius is given as $r=1.5 \times 10^{11}...

Choose the correct answer from among the given ones: the direction of the gravitational intensity at an arbitrary point 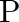$\mathrm{P}$ is indicated by the arrow (i) 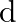$\mathrm{d}$ , (ii) e, (iii) f, (iv) $\mathbf{g}$ .

CBSE, Class 11, Gravitation, NCERT, Physics

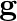(ii) e Reason: From the previous response, we can deduce that, The gravitational intensity at P is directed downwards along 'e' using the logic/explanation

Choose the correct answer from among the given ones: The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig) (i) a, (ii) 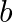$b$ , (iii) c, (iv) 0

CBSE, Class 11, Gravitation, NCERT, Physics

(iii) $\mathrm{C}$ Reason: Gravitational forces on any particle at any position are symmetrically distributed inside a hollow sphere. The upper half of the sphere is, however, deleted in this...

Which of the following symptoms is likely to afflict an astronaut in space
(a) headache,
(b) orientational problem.

CBSE, Class 11, Gravitation, NCERT, Physics

(a). Astronauts may get headaches as a result of the increased blood supply to their faces. (b). Because space has multiple orientations, an astronaut may experience orientational issues.

Which of the following symptoms is likely to afflict an astronaut in space
(a) swollen feet,
(b) swollen face

CBSE, Class 11, Gravitation, NCERT, Physics

(a) Because blood flow to the feet is not increased in zero gravity, the astronaut's feet do not swell. (b) There is more blood supply to the astronaut's face. As a result, the astronaut's face will...

A comet orbits the Sun in a highly elliptical orbit.
(a) potential energy
(b) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.

CBSE, Class 11, Gravitation, NCERT, Physics

(a) Potential energy changes along the path. (b) Total energy will remain constant throughout the orbit.

A comet orbits a sun in a highly elliptical orbit. Does the comet have a constant
(a) linear speed,
(b) angular speed,
(c) angular momentum,
(d) kinetic energy,
(e) potential energy,
(f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the sun.

CBSE, Class 11, Gravitation, NCERT, Physics

A comet in an elliptical orbit around the Sun has constant angular momentum and total energy owing to the Law of Conservation of Energy at all locations, but other variables change. The torque...

A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant
(a) linear speed
(b) angular speed

CBSE, Class 11, Gravitation, NCERT, Physics

(a) The linear speed of the comet changes according to Kepler's second law. The comet's speed will be the quickest when it is closest to the sun, and the slowest when it is farthest away. (b)...

Does the escape speed of a body from the earth depend on
(a) the direction of projection,
(b) the height of the location from where the body is launched?

CBSE, Class 11, Gravitation, NCERT, Physics

The escape speed can be given by the relation, $v=\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}$ (a) The escape speed does not depend on the direction of projection of a body. (b) Because the escape velocity...

Q. 7. Does the escape speed of a body from the earth depend on
(a) the mass of the body,
(b) the location from where it is projected

CBSE, Class 11, Gravitation, NCERT, Physics

The escape speed can be given by the relation, $v=\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}$ (a) The mass of a body has no bearing on its speed of departure from the Earth. (b) The escape speed of a body...

Choose the correct alternative:
(a) If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potential energy.
(b) The energy required to launch an orbiting satellite out of earth’s gravitational influence is more/less than the energy required to project a stationary object at the same height (as the satellite) out of earth’s influence.

CBSE, Class 11, Gravitation, NCERT, Physics

(a) The total energy of an orbiting satellite is negative of its kinetic energy if the zero potential energy is at infinity. (b) The energy required to launch an orbiting satellite out of Earth's...

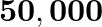Let us assume that our galaxy consists of $2.5 \times 10^{11}$ stars each of one solar mass. How long will a star at a distance of $\mathbf{5 0 , 0 0 0}$ ly from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be $10^{5} \mathrm{ly}$ .

CBSE, Class 11, Gravitation, NCERT, Physics

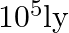Mass of our galaxy is given as $M=2.5 \times 10^{11}$ solar mass 1 Solar mass as we know is, Mass of Sun $=2 \times 10^{30} \mathrm{~kg}$ Mass of our galaxy as we know is $M=2.5 \times 10^{11}...

lo, one of the satellites of Jupiter, has an orbital period of 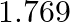$1.769$ days and the radius of the orbit is 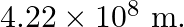$4.22 \times 10^{8} \mathrm{~m} .$ Show that the mass of J upiter is about one-thousandth that of the sun.

CBSE, Class 11, Gravitation, NCERT, Physics

Orbital period of $I0$, is given as $T_{10}=1.769$ days $=1.769 \times 24 \times 60 \times 60 \mathrm{~s}$ Orbital radius of $I0$, is given as $R_{10}=4.22 \times 10^{8} \mathrm{~m}$ Mass of jupiter...

Suppose there existed a planet that went around the Sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?

CBSE, Class 11, Gravitation, NCERT, Physics

Time taken by the earth for one complete revolution is represented by $\mathrm{T}_{\mathrm{E}}$ having value $1$ Year Radius of Earth's orbit is represented by $\mathrm{R}_{\mathrm{E}}$ having value...

Choose the correct alternative:
(a) Acceleration due to gravity is independent of the mass of the earth/mass of the body.
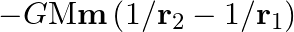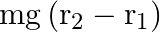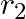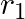(b) The formula $-G\mathrm{M} \mathbf{m}\left(1 / \mathbf{r}_{2}-1 / \mathbf{r}_{1}\right)$ is more/less accurate than the formula $\mathrm{mg}\left(\mathrm{r}_{2}-\mathrm{r}_{1}\right)$ for the difference of potential energy between two points $r_{2}$ and $r_{1}$ distance away from the centre of the earth.

CBSE, Class 11, Gravitation, NCERT, Physics

(a) Acceleration due to gravity is given by the formula: $g=G{{M}_{e}} /{{ {R}_{e}}^{2}}$ is Hence, it is independent of mass of body, but is dependent on mass of earth. (b) Gravitational...

Choose the correct alternative:
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).

CBSE, Class 11, Gravitation, NCERT, Physics

(a) According to the formula g′=g(1-R2h), acceleration decreases. where h is the height and R is the earth's radius (b) According to the formula g′=g(1−Rd),, acceleration decreases. where d is the...

Answer the following: If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull. (you can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of the sun. Why?

CBSE, Class 11, Gravitation, NCERT, Physics

Tidal effects are inversely proportional to the cube of distance, whereas gravitational force is inversely proportional to the square of distance. The moon will have a stronger influence on the...

Answer the following: (a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means? (b) An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?

CBSE, Class 11, Gravitation, NCERT, Physics

(a). No, no technology has yet been devised to shield a body from gravity because gravity is a property of all matter and is independent of medium. As a result, the gravitational forces would be...