Answer : According to the question, the surface tension of the soap solution is S = 2.50 × 10-2 N/m r = 5.00 mm = 5 × 10-3 m We know that the density of the soap solution is ρ = 1.2 × 103 kg/m3 and...
A bat is flitting about in a cave, navigating via ultrasonic beeps. Assume that the sound emission frequency of the bat is 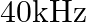 . During one fast swoop directly toward a flat wall surface, the bat is moving at
. During one fast swoop directly toward a flat wall surface, the bat is moving at 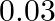 times the speed of sound in the air. What frequency does the bat hear reflected off the wall?
times the speed of sound in the air. What frequency does the bat hear reflected off the wall?
The sound emission frequency of the bat is given as $=40 \mathrm{kHz}$ The velocity of the bat is given as $v_{b}=0.03 \mathrm{v}$ Here, the velocity of the sound in air is $v$ The apparent...
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of the S wave is about 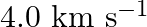 , and that of the
, and that of the  wave is
wave is 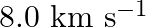 . A seismograph records
. A seismograph records 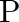 and
and 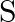 waves from an earthquake. The first P wave arrives 4 min before the first
waves from an earthquake. The first P wave arrives 4 min before the first 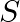 wave. Assuming the waves travel in a straight line, at what distance does the earthquake occur?
wave. Assuming the waves travel in a straight line, at what distance does the earthquake occur?
Let $S$ and $P$ have speeds of $v_{1}$ and $v_{2}$, respectively. The $S$ and $P$ waves take $t_{1}$ and $t_{2}$ seconds to reach the position of the seismograph, respectively. $I=v_{1} t_{1}=v_{2}...
A SONAR system fixed in a submarine operates at a frequency 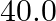 kHz. An enemy submarine moves towards the SONAR with a speed of
kHz. An enemy submarine moves towards the SONAR with a speed of 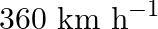 . What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be
. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 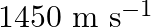 .
.
Frequency of the SONAR system is given as $\mathrm{f}=40 \mathrm{kHz}=40 \times 10^{3} \mathrm{~Hz}$ Speed of sound in water is given as $v=1450 \mathrm{~m} / \mathrm{s}$ Speed of the enemy...
One end of a long string of linear mass density 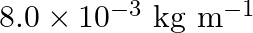 is connected to an electrically driven tuning fork of frequency
is connected to an electrically driven tuning fork of frequency  . The other end passes over a pulley and is tied to a pan containing a mass of
. The other end passes over a pulley and is tied to a pan containing a mass of 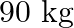 . The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At
. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At  , the left end (fork end) of the string
, the left end (fork end) of the string 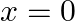 has zero transverse displacement
has zero transverse displacement 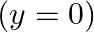 and is moving along positive
and is moving along positive  -direction. The amplitude of the wave is
-direction. The amplitude of the wave is 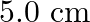 . Write down the transverse displacement y as a function of
. Write down the transverse displacement y as a function of  and
and 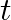 that describes the wave on the string.
that describes the wave on the string.
Linear mass density of the string is given as $\mu=8.0 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}$ Frequency of the tuning fork is given as $=256 \mathrm{~Hz}$ Mass on the pan is given as $90...
A narrow sound pulse (for example, a short pip by a whistle) is sent across a medium. (a) Does the pulse have a definite (i) frequency, (ii) wavelength, (iii) speed of propagation? (b) If the pulse rate is 1 after every 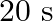 , (that is the whistle is blown for a split of second after every
, (that is the whistle is blown for a split of second after every 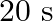 ), is the frequency of the note produced by the whistle equal to
), is the frequency of the note produced by the whistle equal to 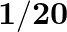 or
or 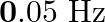 ?
?
(a) The speed of propagation is known, and it is the same as the speed of sound in air. The wavelength and frequency of the signal will be uncertain. (b) The note emitted by a whistle does not have...
A travelling harmonic wave on a string is described by 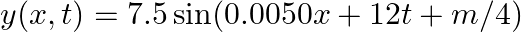
(a) What are the displacement and velocity of oscillation of a point at 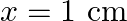 , and
, and 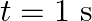 ? Is this velocity equal to the velocity of wave propagation?
? Is this velocity equal to the velocity of wave propagation?
(b) Locate the points of the string which have the same transverse displacements and velocity as the 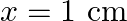 point at
point at 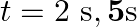 and
and 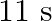
(a) The travelling harmonic wave is given by, $y(x, t)=7.5 \sin (0.0050 x+12 t+\pi / 4)$ At $x=1 \mathrm{~cm}$ and $\mathrm{t}=1 \mathrm{~s}$ $y(1,1)=7.5 \sin (0.0050(1)+12(1)+\pi / 4)$ $=7.5 \sin...
A train, standing in a station-yard, blows a whistle of frequency 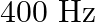 in still air. The wind starts blowing in the direction from the yard to the station with a speed of
in still air. The wind starts blowing in the direction from the yard to the station with a speed of 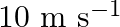 . What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of
. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 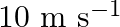 ? The speed of sound in still air can be taken as
? The speed of sound in still air can be taken as 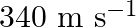
Frequency of the whistle is given as $400 \mathrm{~Hz}$ Speed of wind is given as $\mathrm{v}_{\mathrm{w}}=10 \mathrm{~m} / \mathrm{s}$ Speed of sound in still air is given as $v= 340 \mathrm{~m} /...
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20 °C) is 4.65 × 10–1 N m–1. The atmospheric pressure is 1.01 × 105 Pa. Also give the excess pressure inside the drop.
Ans: According to the question, the Surface tension of mercury is S = 4.65 × 10-1 N m-1 The radius of the drop of mercury is r = 3.00 mm = 3 × 10-3 m And the atmospheric pressure, P0 = 1.01 × 105 Pa...
A train, standing at the outer signal of a railway station blows a whistle of frequency 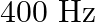 in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of
in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 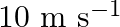 , (b) recedes from the platform with a speed of
, (b) recedes from the platform with a speed of 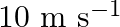 ? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as
? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as  .
.
Frequency of the whistle is given as $=400 \mathrm{~Hz}$ Speed of sound in still air is given as $=340 \mathrm{~m} / \mathrm{s}$ (i) (a)Train approaches the platform at a speed given as...
Explain how:
In a dispersive medium, the shape of a pulse propagating through it gets distorted.
A pulse is made up of electromagnetic waves with different wavelengths. In a dispersive medium, these waves flow at various speeds. Its shape is distorted as a result of this.
Explain how:
(i) A guitar note and violin note are being played at the same frequency, however, we can still make out which instrument is producing which note
(ii) Both transverse and longitudinal wave can propagate through solids, but only longitudinal waves can move through gases.
(i) Overtones are produced differently by the guitar and the violin. Even though the notes from a guitar and a violin vibrate at the same frequencies, it is possible to distinguish between them....
Explain how:
(i) A sound wave’s pressure antinode is a displacement node and vice versa.
(ii) The Ganges river dolphin despite being blind, can manoeuvre and swim around obstacles and hunt down preys.
(i) An antinode is a place where the pressure is lowest and the vibration amplitude is highest. A node, on the other hand, is a place where pressure is highest and vibration amplitude is lowest....
Guitar strings 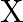 and
and 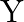 striking the note ‘Ga’ are a little out of tune and give beats at
striking the note ‘Ga’ are a little out of tune and give beats at 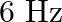 . When the string
. When the string 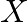 is slightly loosened and the beat frequency becomes
is slightly loosened and the beat frequency becomes 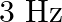 . Given that the original frequency of
. Given that the original frequency of 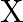 is
is 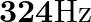 , find the frequency of
, find the frequency of 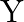 .
.
Frequency of $\mathrm{X}$ is given as $\mathrm{f}_{\mathrm{x}}=324 \mathrm{~Hz}$ Frequency of $Y$ is given as $f_{Y}$ Frequency of the beat is given as $\mathrm{n}=6 \mathrm{~Hz}$ Also,...
One end of A  long tube is closed. Find the harmonic mode of the tube that will be resonantly excited by a source of frequency
long tube is closed. Find the harmonic mode of the tube that will be resonantly excited by a source of frequency 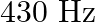 . If both the ends are open, can the same source still produce resonance in the tube? (Sound travels in air at
. If both the ends are open, can the same source still produce resonance in the tube? (Sound travels in air at 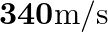 ).
).
Length of the pipe is given as $I=20 \mathrm{~cm}=0.2 \mathrm{~m}$ Frequency of the source is given as $\mathrm{n}^{\text {th }}$ Normal mode of frequency is given as $\mathrm{v}_{\mathrm{N}}=430...
A steel bar of length 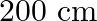 is nailed at its midpoint. The fundamental frequency of the longitudinal vibrations of the rod is
is nailed at its midpoint. The fundamental frequency of the longitudinal vibrations of the rod is 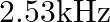 . At what speed will the sound be able to travel through steel?
. At what speed will the sound be able to travel through steel?
Length is given as $I=200 \mathrm{~cm}=2 \mathrm{~m}$ Fundamental frequency of vibration is given as, $\mathrm{v}_{\mathrm{F}}=2.53 \mathrm{kHz}=2.53 \times 10^{3} \mathrm{~Hz}$ The bar is then...
A 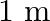 long pipe with a movable piston at one end and an opening at the other will be in resonance with a tuning fork vibrating at
long pipe with a movable piston at one end and an opening at the other will be in resonance with a tuning fork vibrating at 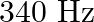 , if the length of the pipe is
, if the length of the pipe is 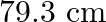 or
or 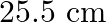 . Calculate the speed of sound in air. Neglect the edge effects.
. Calculate the speed of sound in air. Neglect the edge effects.
Frequency of the turning fork is given as $\mathrm{v}_{\mathrm{F}}=340 \mathrm{~Hz}$ Length of the pipe is given as $l_{1}=0.255 \mathrm{~m}$ Due to the presence of a piston at one end, the supplied...
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
Answer : (a) According to the question, the length of the film which is supporting the weight is = 40 cm = 0.4 m. and the total weight supported = 4.5 x 10-2 N. We know that the film has two free...
A string clamped at both its ends is stretched out, it is then made to vibrate in its fundamental mode at a frequency of 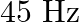 . The linear mass density of the string is
. The linear mass density of the string is 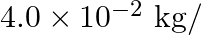 m and its mass is
m and its mass is 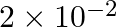 kg. Calculate:
kg. Calculate:
(i) the velocity of a transverse wave on the string,
(ii) the tension in the string.
Mass of the string is given as $m=2 \times 10^{-2} \mathrm{~kg}$ Linear density of the string is given s $=4 \times 10^{-2} \mathrm{~kg}$ Frequency is given as $\mathrm{v}_{\mathrm{F}}=45...
Present below are functions of  and
and  to describe the displacement (longitudinal or transverse) of an elastic wave. Identify the ones describing ( a ) a stationary wave, ( b ) a travelling wave and ( c) neither of the two:
to describe the displacement (longitudinal or transverse) of an elastic wave. Identify the ones describing ( a ) a stationary wave, ( b ) a travelling wave and ( c) neither of the two:
(i) 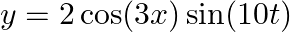
(ii) 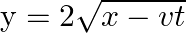
(i) Because the harmonic terms $\omega t$ and $k x$ exist individually, this equation depicts a stationary wave. (ii) There are no harmonic terms in this equation. As a result, it is neither a...
Present below are functions of  and
and  to describe the displacement (longitudinal or transverse) of an elastic wave. Identify the ones describing ( a ) a stationary wave, ( b ) a travelling wave and ( c) neither of the two:
to describe the displacement (longitudinal or transverse) of an elastic wave. Identify the ones describing ( a ) a stationary wave, ( b ) a travelling wave and ( c) neither of the two:
(ii) 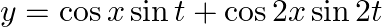
(i) The harmonic terms $\omega t$ and $kx$ in the combination of $k x-w t$ explain a traveling wave in this equation. (ii) The harmonic terms $\omega t$ and $kx$ exist individually in the equation....
Considering the wave, 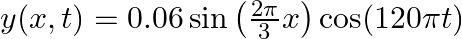
Answer the following questions;
(a) Are all the points in the wire oscillating at the same values of (i) frequency, (ii) phase, (iii) amplitude? Justify your answers.
(b) Calculate the amplitude of a point  away from one end?
away from one end?
(a) Because both ends of the wire are clamped, the ends act as nodes, and the entire wire vibrates as a single segment. Thus, (i) Except at the wire's ends, where the frequency is 0, all of the...
The transverse displacement of a wire (clamped at both its ends) is described as : 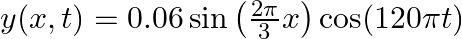 The mass of the wire is
The mass of the wire is 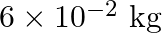 and its length is
and its length is 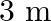 .
.
Provide answers to the following question:
Calculate the wire’s tension.
[X and  are in meters and
are in meters and 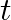 in secs]
in secs]
As we know, The standard equation of a stationary wave is known as, $y(x, t)=2 a \sin k x \cos w t$ Given equation is, $y(x, t)=0.06 \sin \left(\frac{2 \pi}{3} x\right) \cos (120 \pi t)$ It is...
The transverse displacement of a wire (clamped at both its ends) is described as : 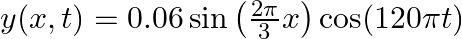 The mass of the wire is
The mass of the wire is 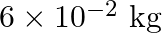 and its length is
and its length is 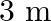 .
.
Provide answers to the following questions:
(i) Is the function describing a stationary wave or a travelling wave?
(ii) Interpret the wave as a superposition of two waves travelling in opposite directions. Find the speed, wavelength and frequency of each wave.
As we know, The standard equation of a stationary wave is known as, $y(x, t)=2 a \sin k x \cos w t$ Given equation is, $y(x, t)=0.06 \sin \left(\frac{2 \pi}{3} x\right) \cos (120 \pi t)$ It is...
A travelling harmonic wave is given as: 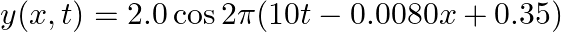 . What is the phase difference between the oscillatory motion of two points separated by a distance of:
. What is the phase difference between the oscillatory motion of two points separated by a distance of:
(i) 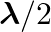 ,
,
(ii) 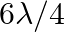
[ 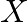 and
and  are in
are in 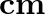 and
and 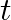 is in secs
is in secs ![Rendered by QuickLaTeX.com ]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-478d84af1027ee3593251b323a3fb181_l3.png) .
.
Equation for a travelling harmonic wave is given as, $\begin{array}{l} y(x, t)=2.0 \cos 2 \pi(10 t-0.0080 x+0.35) \\ =2.0 \cos (20 \pi t-0.016 \pi x+0.70 \pi) \end{array}$ where, Propagation...
A travelling harmonic wave is given as: 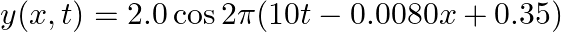 . What is the phase difference between the oscillatory motion of two points separated by a distance of:
. What is the phase difference between the oscillatory motion of two points separated by a distance of:
(i) 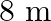 ,
,
(ii) 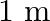
[ 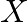 and
and  are in
are in  and
and  is in secs
is in secs ![Rendered by QuickLaTeX.com ]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-478d84af1027ee3593251b323a3fb181_l3.png) .
.
Equation for a travelling harmonic wave is given as, $\begin{array}{l} y(x, t)=2.0 \cos 2 \pi(10 t-0.0080 x+0.35) \\ =2.0 \cos (20 \pi t-0.016 \pi x+0.70 \pi) \end{array}$ where, Propagation...
For the wave, 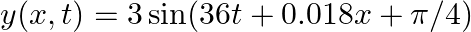 plot the displacement (
plot the displacement (  ) versus (t) graphs for
) versus (t) graphs for  0,2 and
0,2 and 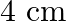 .
.
(i) Give the shapes of these plots.
(ii) With respect to which aspects (amplitude, frequency or phase) does the oscillatory motion in a travelling wave differ from one point to another?
Given wave is, $y(x, t)=3 \sin (36 t+0.018 x+\pi / 4)$.....(1) Putting $x=0$, the equation becomes: $y(0, t)=3 \sin (36 t+0+\pi / 4)$.....(2) Also, $\omega=2 \pi / \mathrm{t}=36 \mathrm{rad} /...
A transverse harmonic wave on a wire is expressed as: 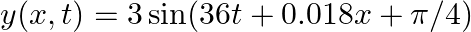
Calculate the smallest distance between two adjacent crests in the wave.
[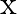 and
and 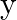 are in
are in 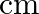 and
and 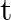 in seconds. Assume the left to right direction as the positive direction of
in seconds. Assume the left to right direction as the positive direction of ![Rendered by QuickLaTeX.com \mathrm{x}]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7eec0f19e3a8a19059d43c95ee5abebd_l3.png)
Given function is, $(x, t)=3 \sin (36 t+0.018 x+\pi / 4)$ The smallest distance between two adjacent crests in the wave can be calculated as, $\lambda=2 \pi / \mathrm{k}=2 \mathrm{~m} / 0.018$ $=349...
A transverse harmonic wave on a wire is expressed as: 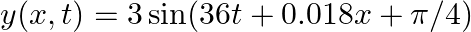
i) Find its frequency and amplitude.
ii) Give the initial phase at the origin.
[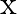 and
and 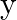 are in
are in 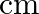 and
and 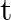 in seconds. Assume the left to right direction as the positive direction of
in seconds. Assume the left to right direction as the positive direction of ![Rendered by QuickLaTeX.com \mathrm{x}]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7eec0f19e3a8a19059d43c95ee5abebd_l3.png)
Given function is, $(x, t)=3 \sin (36 t+0.018 x+\pi / 4)$ i) Amplitude of the wave is given as $a=3 \mathrm{~cm}$ Frequency of the wave can be calculated as $v=\omega / 2 \pi$ $36 / 2 \pi=5.7...
A transverse harmonic wave on a wire is expressed as: 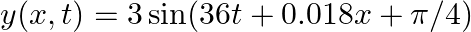
(i) Is it a stationary wave or a travelling one?
ii) If it is a travelling wave, give the speed and direction of its propagation.
[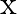 and
and 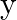 are in
are in 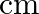 and
and 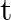 in seconds. Assume the left to right direction as the positive direction of
in seconds. Assume the left to right direction as the positive direction of ![Rendered by QuickLaTeX.com \mathrm{x}]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7eec0f19e3a8a19059d43c95ee5abebd_l3.png)
Given function is, $(x, t)=3 \sin (36 t+0.018 x+\pi / 4)$ i) The equation of a progressive wave travelling from right to left is known as, $y(x, t)=a \sin (\omega t+k x+\Phi)$ On comparing equation...
An ultrasonic scanner operating at 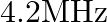 is used to locate tumours in tissues. If the speed of sound is
is used to locate tumours in tissues. If the speed of sound is 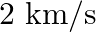 in a certain tissue, calculate the wavelength of sound in this tissue.
in a certain tissue, calculate the wavelength of sound in this tissue.
Speed of sound in the tissue is given as, $v_{T}=2 \mathrm{~km} / \mathrm{s}=2 \times 10^{3} \mathrm{~m} / \mathrm{s}$ Operating frequency of the scanner is given as $\mathrm{v}=4.2 \mathrm{MHz}=4.2...
A bat emits ultrasonic sound of frequency 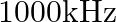 in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound? Speed of sound in air is
in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound? Speed of sound in air is 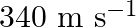 and in water
and in water 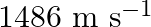
Frequency of the ultrasonic sound is given as $\mathrm{v}=1000 \mathrm{kHz}=10^{6} \mathrm{~Hz}$ Speed of sound in air is given as $v_{A}=340 \mathrm{~m} / \mathrm{s}$ As we know, (a) The wavelength...
We know that the function 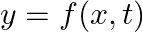 represents a wave travelling in one direction, where
represents a wave travelling in one direction, where  and
and 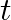 must appear in the combination
must appear in the combination 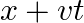 or
or 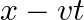 or i.e.
or i.e. 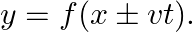 Is the converse true? Can the following functions for y possibly represent a travelling wave:
Is the converse true? Can the following functions for y possibly represent a travelling wave:
(i)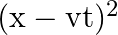
(ii) ![Rendered by QuickLaTeX.com \log \left[(x+v t) / x_{0}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-99d2bcfc07e0da1a668137fffad738d8_l3.png)
(iii) 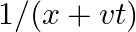
No, the opposite is not true, because a wave function representing a travelling wave must have a finite value for all $x$ and $t$ values. None of the functions above satisfy the criteria, hence none...
Using the formula 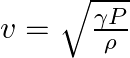 explain why the speed of sound in air increases with humidity.
explain why the speed of sound in air increases with humidity.
Given values are, $v=\sqrt{\frac{\gamma P}{\rho}}$ $\Rightarrow \mathrm{P}=\frac{\rho R T}{M}$ $\Rightarrow \frac{P}{\rho}=\frac{R T}{M}$ The effective density of the air decreases as humidity...
Using the formula 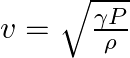 explain why the speed of sound in air
explain why the speed of sound in air
(a) does not depend upon pressure.
(b) increases with temperature and humidity.
Given values are, $v=\sqrt{\frac{\gamma P}{\rho}}$ $\Rightarrow \mathrm{P}=\frac{\rho R T}{M}$ $\Rightarrow \frac{P}{\rho}=\frac{R T}{M}$ (a) For a gas at a constant temperature, $\frac{P}{\rho}=...
Steel wire has a length of 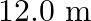 and a mass of
and a mass of 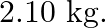 What should be the tension in the wire so that the speed of a transverse wave on the wire equals the speed of sound in dry air at
What should be the tension in the wire so that the speed of a transverse wave on the wire equals the speed of sound in dry air at 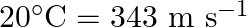
Length of the steel wire is given as $I=12 \mathrm{~m}$ Mass of the steel wire is given as $\mathrm{m}=2.0 \mathrm{~kg}$ Velocity of the transverse wave is given as $\mathrm{v}=343 \mathrm{~m} /...
A stone dropped from the top of a tower of height 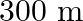 splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is
splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 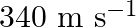 ?
? 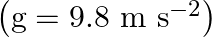
Height of the bridge is given as $s=300 \mathrm{~m}$ Initial velocity of the stone is given as $u=0$ Acceleration is known as $a=g=9.8 \mathrm{~m} / \mathrm{s}^{2}$ Speed of sound in air is given as...
A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film ?
Answer : The maximum weight the film can support, W = 1.5 × 10-2 N Length of the slider, l = 30 cm = 0.3 m Total length of liquid film, l = 2 x 30 cm = 60 cm = 0.6 m because the liquid film has two...
The cylindrical tube of a spray pump has a cross-section of 8.0 cm2 one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min–1, what is the speed of ejection of the liquid through the holes?
Answer : According to the question, Number of holes, n = 40 Spray pump's cross-sectional area, A1 = 8 cm -2= 8 × 10-4 m-2 Radius of each hole, r = 0.5 × 10-3 m Cross-sectional area the said hole, a...
Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect ? Why ?
Answer : Figure (a) is incorrect. The reason for this is that the velocity of liquid flow near the kink is high, hence applying Bernoulli's theorem, the pressure is low. As a result, when there is a...
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s–1 and 63 m s-1 respectively. What is the lift on the wing if its area is 2.5 m2 ? Take the density of air to be 1.3 kg m -3
Answer : According to the question, the Speed of wind on the upper side of the wing is V1 = 70 m/s And the speed of wind on the lower side of the wing is V2 = 63 m/s We are given that the area of...
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 × 10–3 kg s–1, what is the pressure difference between the two ends of the tube? (Density of glycerine = 1.3 × 103 kg m–3 and viscosity of glycerine = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct].
Answer : According to the question, the Length of the horizontal tube, l = 1.5 m and the radius of the tube is r = 1 cm = 0.01 m Therefore diameter of the tube becomes- d = 2r = 0.02 m It is given...
A refrigerator is to maintain eatables kept inside at 9 degrees C. If room temperature is 36 degrees C, calculate the coefficient of performance.
Solution: Given, Temperature inside the refrigerator, T1 = 90 C Temperature in kelvin = 273 + 9= 282 K Room temperature, T2 = 360 C Temperature in kelvin = 273 + 36= 309 K Coefficient of performance...
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain
Answer : No, it doesn't matter if Bernoulli's equation is applied using gauge pressures rather than absolute pressures, as long as the atmospheric pressures at the two sites where Bernoulli's...
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Fig. Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F.
Solution: From figure, DEF is the area of the gas's total work done from D through E and F. Area of ∆DEF = (1/2) x DE x EF Where, DF = Change in pressure = 600 N/m2 – 300 N/m2= 300 N/ m2 FE = Change...
Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain.
Answer : Bernoulli's equation cannot be used to describe the flow of water in a river since it only applies to perfect liquids in a streamlined flow, whereas the water in a stream is turbulent.
In the previous problem, if 15.0 cm of water and spirit each is further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)
Answer ; According to the question, h1 = 10.0 cm and ρ1 = 1 g cm-3 and for the spirit column in another arm of the U-tube, h2 = 12.5 cm We have to determine the value of p2 Let h be the difference...
An electric heater supplies heat to a system at a rate of 100W. If system performs work at a rate of 75 joules per second. At what rate is the internal energy increasing?
Given: As we know that the law of conservation of energy states that all energy is conserved. The total energy is equal to the sum of work done and internal energy. ΔQ = ΔW + ΔU Heating at a rate of...
A steam engine delivers 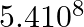 J of work per minute and services
J of work per minute and services 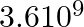 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
Solution: Given Amount of work done by the steam engine in one minute, W = 5.4 x 108 J Heat supplied from the boiler, H = 3.6 x 109 J...
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:(c) What is the change in the temperature of the gas? (d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
Answer: c) The gas's temperature will not change. Because gas expands, it does not operate. In this operation, the gas's temperature will not change....
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following: (a) What is the final pressure of the gas in A and B? (b) What is the change in internal energy of the gas?
Answer: (a). By allowing gas to flow from cylinder P to cylinder Q, the volume of gas will be doubled because both cylinders have identical capacity. Because pressure is inversely proportional to...
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Answer : According to the question, the height of the spirit column is h1 = 12.5 cm = 0.125 m And the height of the water column is h2 = 10 cm = 0.1 m Let A and B represent the points of contact...
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J)
Given 22.3 joules of work (W) are performed on the system while the gas transitions between states A and B. This is an example of an adiabatic process. As a result, the change in heat is zero. So,...
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?
Answer: The cylinder is fully isolated from the rest of the environment. There is no heat exchange between the system (cylinder) and its surroundings as a result of the design....
Explain why: (c) Air pressure in a car tyre increases during driving. (d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.
Answer: c)Because air molecules move, the temperature inside tires rises as the driver is moving. And, per Charles' law, temperature equals the pressure....
Explain why (a) Two bodies at different temperatures T1 and T2 if brought in thermal contact do not necessarily settle to the mean temperature (T1 + T2)/2. (b) The coolant in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.
Answer i) When two bodies with different temperatures, T1 and T2, are brought into thermal contact, heat flows from the hotter body to the cooler body until both bodies reach equilibrium, i.e., both...
What amount of heat must be supplied to 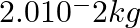 of nitrogen (at room temperature) to raise its temperature by 45 °C at constant pressure? (Molecular mass of
of nitrogen (at room temperature) to raise its temperature by 45 °C at constant pressure? (Molecular mass of 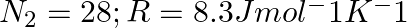 .)
.)
Solution: Given, The mass of nitrogen is equal to 2 x 10-2 kg =20 g Temperature increase = T. = 45 degrees Celsius Q = the amount of heat necessary Q = nCT is a mathematical expression....
A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents
Ans: Given: According to the question, the maximum stress that a structure can handle is P = 109 Pa And the depth of the sea is d = 3 km = 3 × 103 m We also have the density of water as ρ...
A geyser heats water flowing at the rate of 3.0 litres per minute from 27 °C to 77 °C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0 × 104 J/g?
Solution: Given The water is moving at a rate of 3.0 litres per minute. The geyser heats the water, elevating the temperature from 27 degrees Celsius to 77 degrees Celsius as a result. Initial...
Toricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m–3. Determine the height of the wine column for normal atmospheric pressure
Ans: According to the question, the density of mercury is ρ1 = 13.6 × 103 kg/m3 And the height of the mercury column is h1 = 0.76 m Also, the density of French wine is : ρ2 = 984 kg/m3 We have to...
A hot ball cools from 90 °C to 10 °C in 5 minutes. If the surrounding temperature is 20°C, what is the time taken to cool from 60 °C to 30 °C?
Answer: Newton's law of cooling states that the rate of cooling is directly proportional to the difference in temperature between two points. Here, average of $90 \mathrm{C}$ and $40^{\circ}...
Answer the following questions based on the P-T phase diagram of carbon dioxide: (c) What are the critical temperature and pressure for Carbon dioxide? What is its significance? (d) Is Carbon dioxide solid, liquid or gas at (a) –70 °C under 1 atm, (b) –60 °C under 10 atm, (c) 15 °C under 56 atm?
Answer: c) As a result, the critical temperature and pressure of carbon dioxide are 31.1 degrees Celsius and 73.0 atmospheres, respectively. Carbon dioxide will not liquefy above this temperature,...
Answer the following questions based on the P-T phase diagram of carbon dioxide: (a) At what temperature and pressure can the solid, liquid and vapour phases of 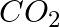 co-exist in equilibrium? (b) What is the effect of the decrease of pressure on the fusion and boiling point of
co-exist in equilibrium? (b) What is the effect of the decrease of pressure on the fusion and boiling point of  ?
?
Answer: (a) The liquid and vapor phases of $CO_2$ coexist at the triple point temperature and pressure of − 56.6 degrees Celsius and 5.11 atmospheres. (b) When the pressure of $CO_2$...
A body cools from 80 °C to 50 °C in 5 minutes. Calculate the time it takes to cool from 60 °C to 30 °C. The temperature of the surroundings is 20 °C.
Solution: Given: In this question, the initial temperature of the body is 80 degrees Celsius, and the final temperature of the body is 50 degrees Celsius. (T1 + T2)/2 is the average temperature. Avg...
Explain why : (e) heating systems based on the circulation of steam are more efficient in warming a building than those based on the circulation of hot water
Answer: (e) Steam at 100 degrees Celsius is significantly hotter than water at 100 degrees Celsius. This is due to the fact that steam contains a significant amount of heat in the form of latent...
Explain why : (c) an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace (d) the earth without its atmosphere would be inhospitably cold
Answer: (c) The radiation energy emitted by a red hot iron piece placed in a furnace can be calculated using the equation E=σT4...
Explain why : (a) a body with large reflectivity is a poor emitter (b) a brass tumbler feels much colder than a wooden tray on a chilly day
Answer: (a) A body with high reflectivity absorbs heat radiation poorly. Poor absorbers emit poor radiations. So a reflective body is a poor emitter. (b) Brass conducts heat well while wood does...
A brass boiler has a base area of 0.15 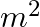 and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass =
and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass = 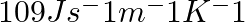 ; Heat of vaporisation of water = 2256 × 103
; Heat of vaporisation of water = 2256 × 103 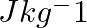 .
.
Solution: Given: A= 0.15 $m^2$ is the surface area of the brass boiler's base. D is the boiler's thickness, which is equal to 1 cm=0.01 m. The rate at which the brass boiler boils water is R=6.0...
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter of 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer : According to the question, the radius of the heel, r = d/2 = 0.005 m And the mass of the lady (m) = 50 kg We know that the expression for the Area of the heel can be written as - A = πr2 =...
A ‘thermacole’ icebox is a cheap and an efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side 30 cm has a thickness of 5.0 cm. If 4.0 kg of ice is put in the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45 °C, and the co-efficient of thermal conductivity of thermacole is 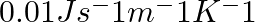 . [Heat of fusion of water = 335 × 103
. [Heat of fusion of water = 335 × 103 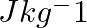 ]
]
Solution: Given: Side of the cubical icebox, s =30 cm=3 x 10-2 m Thickness of the icebox, L =5.0 cm=0.05 m Mass of ice kept in the icebox, m=4 kg Time, t=6 h=6×60×60 = 21600 Outside temperature, T1=...
A child running a temperature of 101°F is given an antipyrin (i.e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to 98 °F in 20 minutes, what is the average rate of extra evaporation caused, by the drug. Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of human body is approximately the same as that of water, and the latent heat of evaporation of water at that temperature is about 580 cal g–1.
Solution: Given: The initial temperature of the child, Ti =101o F The final temperature of the child, Tf=98oF Decrease in the temperature, △T=(101−98)= 30 F = 3×(5/9)= 1.670 C Mass of the child,...
Given below are observations on molar specific heats at room temperature of some common gases.Generally, the specific heat of a monoatomic gas is 2.92 cal (mol K )‑1 , which is significantly lower from the specific heat of the above gases. Explain. It can be observed that chlorine has little larger value of specific heat, what could be the reason?
Answer: The diatomic molecules in the preceding list can move in translation, vibration, and rotation. A monoatomic gas can only move translationally. Heat is required to increase translational,...
In an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150 °C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27 °C. The final temperature is 40 °C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for the specific heat of the metal?
Solution: Given the information in the question: Mass of the metal block, m = 0.20 kg = 200 g The initial temperature of the metal block, T1 = 1500C The final temperature of the metal block, T2 =...
A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500 °C and then placed on a large ice block. What is the maximum amount of ice that can melt?
Solution: Given, Mass of the copper block, m = 2.5 kg The temperature of the block, ΔT= 5000 C Specific heat of copper, c= 0.39 J g–1 K–1 Latent Heat of fusion of water, L = 335 J g–1 Let m’ be the...
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings.
Solution: Given: Power = 10 kW Mass of the small aluminium block, m = 8 kg = 8 x 103 g Time = 2.5×60=150 s Specific heat of aluminium, c= 0.91 J g–1 K–1. Total energy =P×t=104 ×150=15×105 J As 50%...
The coefficient of volume expansion of glycerine is 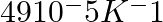 . What is the fractional change in its density for a 30 °C rise in temperature?
. What is the fractional change in its density for a 30 °C rise in temperature?
Given: Coefficient of volume expansion of glycerine, $\alpha_{v}=49 \times 10^{-5} \mathrm{~K}^{-1}$ Rise in temperature, $\Delta \mathrm{T}=30^{\circ} \mathrm{C}$ Fractional change in volume...
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 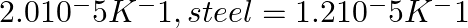 .
.
Solution: Given: Length of the brass rod = length of the steel rod = L0 = 50 cm Diameter of the brass rod = diameter of the steel rod = 3 mm Initial temperature ( T1) = 40°C Final temperature ( T2)...
A brass wire 1.8 m long at 27 °C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of –39 °C, what is the tension developed in the wire, if its diameter is 2.0 mm? Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1; Young’s modulus of brass = 0.91 × 1011 Pa.
Answer: Given: Initial temperature, T1=27oC Length of the brass wire at 27oC, l =1.8m Final temperature, T2=- 390C Diameter of the wire, d=2.0mm=2×10−3m Coefficient of linear expansion of...
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 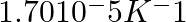 .
.
Solution: Given in the question: Diameter of hole ( D1) = 4.24 cm Initial Temperature, T1 = 27.0 °C = 27+ 273 = 300 K Final temperature, T2 =227 °C = 227+ 273 = 500K Let the diameter of the hole at...
A large steel wheel is to be fitted on to a shaft of the same material. At 27 °C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume the coefficient of linear expansion of the steel to be constant over the required temperature range: 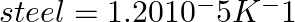 .
.
Solution: Given the information in the question: Temperature, T= 27 °C The outer diameter of the shaft at 27 °C is d1 = 8.70 cm The diameter of the central hole in the wheel at 27 °C is d2 = 8.69 cm...
A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0 °C? Coefficient of linear expansion of steel = 1.20 × 10–5 K–1
Solution: Given: The temperature at which tape is calibrated: T = 27 °C At the temperature of 27 °C, the length of the tape is 1m = 100 cm T1 = 45 °C The length of the tape is 63 cm when the...
Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made: a) What is the absolute temperature of the normal melting point of sulphur as read by thermometers A and B? (b) What do you think is the reason behind the slight difference in answers of thermometers A and B? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?
Solution: (a) Given: Triple point of water, T= 273.16K. Pressure in thermometer A at the triple point, PA =1.25×105 Pa Normal melting point of sulphur = T1 Pressure in thermometer A at this...
(c) The absolute temperature (Kelvin scale)  is related to the temperature tc on the Celsius scale by tc = T – 273.15. Why do we have
is related to the temperature tc on the Celsius scale by tc = T – 273.15. Why do we have 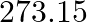 in this relation, and not 273.16? (d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale?
in this relation, and not 273.16? (d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale?
Solution: (iii) The relationship exists because the melting point of ice equates to $273.15 K$ on the Kelvin scale, and the triple point of water corresponds to $273.16 K$ on the Kelvin scale. (iv)...
(a) The triple-point of water is a standard fixed point in modern thermometer. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale)? (b) There were two fixed points in the original C elsius scale as mentioned above which were assigned the number 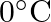 and
and 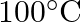 , respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number
, respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 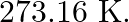 What is the other fixed point on this (Kelvin) scale?
What is the other fixed point on this (Kelvin) scale?
Solution: i) Due to the fact that the melting and boiling points of water fluctuate with changes in pressure, the temperature of the triple point of water is not considered to be a standard fixed...
The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law: ![Rendered by QuickLaTeX.com \mathbf{R}=\mathbf{R}_{\mathrm{o}}\left[1+\alpha\left(\mathrm{T}-\mathrm{T}_{0}\right)\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7d41138edf78cb4422493eb359a7f99c_l3.png) The resistance is
The resistance is 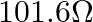 at the triple-point of water
at the triple-point of water 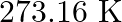 , and
, and 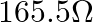 at the normal melting point of lead (600.5 K). What is the temperature when the resistance is
at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 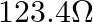 ?
?
Solution: Given information in the question, Triple point temperature, $T_{0}=273.16 \mathrm{~K}$ Resistance at the triple point, $R_{0}=101.6 \Omega$ Normal melting point of lead, $T_{1}=600.5...
Two absolute scales A and B have triple points of water defined to be 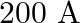 and
and 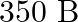 . What is the relation between TA and TB?
. What is the relation between TA and TB?
Solution: Given: Triple point of water on absolute scale $\mathrm{B}, \mathbf{T}_{2}=\mathbf{4 0 0} \mathbf{~ B}$ Triple point of water on absolute scale $A, T_{1}=200 A$ Triple point of water on...
A string of mass 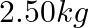 is under a tension of
is under a tension of 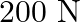 . The length of the stretched string is
. The length of the stretched string is 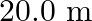 . If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
Mass of the string is given as $M=2.50 kg$ Tension in the string is given as $T=200 N$ Length of the string is given as $\mid=20.0 m$ Mass per unit length will be, $\mu=\mathrm{M} / \mathrm{I}=5 /...
A mild steel wire of cross-sectional area 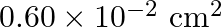 and length
and length 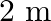 is stretched ( not beyond its elastic limit ) horizontally between two columns. If a
is stretched ( not beyond its elastic limit ) horizontally between two columns. If a 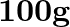 mass is hung at the midpoint of the wire, find the depression at the midpoint.
mass is hung at the midpoint of the wire, find the depression at the midpoint.
Solution: Let $Y Z$ be a mild steel wire with a cross sectional area of $A=0.60 \times 10^{-2} cm^{2}$ and a length of 2m. As indicated in the image, a mass of $m=100g=0.1kg$ is hanged from the...
The Marina trench is located in the Pacific Ocean, and at one place it is nearly eleven km beneath the surface of the water. The water pressure at the bottom of the trench is about 
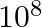 Pa. A steel ball of initial volume
Pa. A steel ball of initial volume 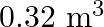 is dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches the bottom?
is dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches the bottom?
Water pressure at the bottom of the trench is given as $\mathrm{p}=1.1 \times 10^{8} \mathrm{~Pa}$ Initial volume of the steel ball is given as $V=0.32 \mathrm{~m}^{3}$ Bulk modulus of steel is...
Two strips of metal are riveted together at their ends by four rivets, each of diameter 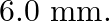 What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed
What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed  Pa? Assume that each rivet is to carry one-quarter of the load.
Pa? Assume that each rivet is to carry one-quarter of the load.
Diameter of the metal strips is given as $6 \mathrm{~mm}=6 \times 10^{-3} \mathrm{~m}$ Radius will be then, $r=3 \times 10^{-3} \mathrm{~m}$ Shearing stress on the rivet is given as $6.9 \times...
A mild steel wire of length 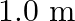 and cross-sectional area
and cross-sectional area 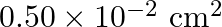 is stretched, well within its elastic limit, horizontally between two pillars. A mass of
is stretched, well within its elastic limit, horizontally between two pillars. A mass of  is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
Water pressure at the bottom is given as, $p=1000 a t m=1000 \times 1.013 \times 10^{5}$ Pa $p=1.01 \times 10^{8} \mathrm{~Pa}$ Initial volume of the steel ball is given as $V=0.30 \mathrm{~m}^{3}$...
A rod of length  having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in the figure. The cross-sectional areas of wires
having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in the figure. The cross-sectional areas of wires  and
and  are
are 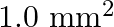 and
and 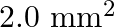 , respectively. At what point along the rod should a mass
, respectively. At what point along the rod should a mass 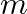 be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
Solution: Cross-sectional area of wire A is given as $a_{1}=1.0 \mathrm{~mm}^{2}=1.0 \times 10^{-6} \mathrm{~m}^{2}$ Cross-sectional area of wire B is given as $a_{2}=2 m m^{2}=2 \times 10^{-6}...
Anvils made of single crystals of diamond, with the shape as shown in the figure, are used to investigate the behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?
The diameter of the flat faces at the narrow end of the anvil is given as, $d=0.50mm=0.5\times 10^{-3} m$ Radius will be, $r=d/2=0.25\times 10^{-3} m$ Compressional force is given as $F=50000N$...
How much should the pressure on a litre of water be changed to compress it by 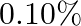 ?
?
Volume of water is given as $V=1$ litre Water should be compressed by $0.10 \%$ is given The fractional change in volume will be, $\Delta \mathrm{V} N=(0.1 / 100) \times 1=10^{-3}$ Bulk modulus,...
Determine the volume contraction of a solid copper cube, 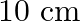 on an edge, when subjected to a hydraulic pressure of
on an edge, when subjected to a hydraulic pressure of 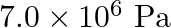 .
.
Side of the copper cube is given as $a=10 \mathrm{~cm}$ Therefore, Volume of the copper cube will be, $\mathrm{V}=\mathrm{a}^{3}=10^{-3} \mathrm{~m}^{3}$ Hydraulic pressure is given as...
What is the density of water at a depth where pressure is 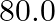 atm, given that its density at the surface is
atm, given that its density at the surface is 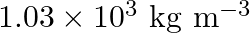 ?
?
Let the depth be 'd' Pressure at the given depth is given as $p=60\times1.01\times10^{5}Pa$ Density of water at the surface is given as $\rho_{1}=1.03\times10^{3}$ $kg$ $m^{3}$ Let $\rho_{2}$ be the...
Compute the bulk modulus of water from the following data: Initial volume = 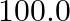 litre, Pressure increase
litre, Pressure increase 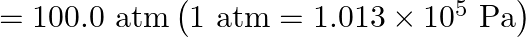 , Final volume
, Final volume 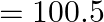 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
Initial volume is given as $V_{1}=100.0$ litre $=100.0 \times 10^{-3} \mathrm{~m}^{3}$ Final volume is given as $V_{2}=100.5$ litre $=100.5 \times 10^{-3} \mathrm{~m}^{3}$ $=101.3 \times 10^{5}...
A  mass, fastened to the end of a steel wire of unstretched length
mass, fastened to the end of a steel wire of unstretched length 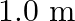 , is whirled in a vertical circle with an angular velocity of
, is whirled in a vertical circle with an angular velocity of 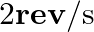 at the bottom of the circle. The crosssectional area of the wire is
at the bottom of the circle. The crosssectional area of the wire is 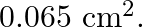 Calculate the elongation of the wire when the mass is at the lowest point of its path.
Calculate the elongation of the wire when the mass is at the lowest point of its path.
Mass is given as $m=14.5 \mathrm{~kg}$ Length of the steel wire is given as $\mid=1 \mathrm{~m}$ Angular velocity is given as $v=2$ rev/s Cross-sectional area of the wire is given as $A=0.065 \times...
A rigid bar of mass 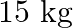 is supported symmetrically by three wires each
is supported symmetrically by three wires each 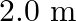 long. Those at each end are of copper and the middle one is of iron. Determine the ratios of their diameters if each is to have the same tension.
long. Those at each end are of copper and the middle one is of iron. Determine the ratios of their diameters if each is to have the same tension.
The extension of each wire will be the same because the stress on the wires is the same. Now that the wires are the same length, the tension on them will be the same. Now, we know: $Y=Stress /...
A steel cable with a radius of 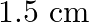 supports a chairlift at a ski area. If the maximum stress is not to exceed
supports a chairlift at a ski area. If the maximum stress is not to exceed 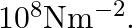 What is the maximum load the cable can support?
What is the maximum load the cable can support?
Radius of the steel cable is given as $r=1.5 \mathrm{~cm}=0.015 \mathrm{~m}$ Cross-sectional area of the cable will be, $\pi r^{2}=3.14 \times(0.015)^{2}$ $=7.06 \times 10^{-4} \mathrm{~m}$ Maximum...
Area of the copper piece is given as $A=19.1 \times 10^{-3} \times 15.2 \times 10^{-3}=2.9 \times 10^{-4} \mathrm{~m}^{2}$ Tension force applied on the piece of copper is given as $\mathrm{F}=44,500...
Four identical hollow cylindrical columns of mild steel support a big structure of a mass 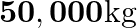 . The inner and outer radii of each column are
. The inner and outer radii of each column are 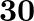 and
and 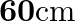 respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
Mass of the big structure is given as $M=50,000 \mathrm{~kg}$ Total force exerted on the four columns will be equal to the total weight of the structure, that is, $50000 \times 9.8 \mathrm{~N}$ The...
The edge of an aluminium cube is 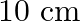 long. One face of the cube is firmly fixed to a vertical wall. A mass of
long. One face of the cube is firmly fixed to a vertical wall. A mass of 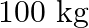 is then attached to the opposite face of the cube. The shear modulus of aluminium is
is then attached to the opposite face of the cube. The shear modulus of aluminium is 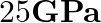 . What is the vertical deflection of this face?
. What is the vertical deflection of this face?
Edge of the aluminium cube is given as $L=10 \mathrm{~cm}=10 / 100=0.1 \mathrm{~m}$ Area of each face wil be, $A=(0.1)^{2}=0.01 \mathrm{~m}^{2}$ Mass attached to the opposite face of the cube is...
Two wires of diameter 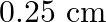 , one made of steel and the other made of brass are loaded as shown in Fig. The unloaded length of steel wire is
, one made of steel and the other made of brass are loaded as shown in Fig. The unloaded length of steel wire is 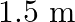 and that of brass wire is
and that of brass wire is 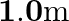 . Compute the elongations of the steel and the brass wires. [Young’s modulus of steel is
. Compute the elongations of the steel and the brass wires. [Young’s modulus of steel is 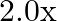
![Rendered by QuickLaTeX.com \left.10^{11} \mathrm{~Pa} .\left(1 \mathrm{~Pa}=1 \mathrm{~N} \mathrm{~m}^{2}\right)\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-36c8cbb599d2f5fc96ae57f00cbbd2ee_l3.png)
Diameter of the two wires is given as $d=0.25 \mathrm{~m}$ Radius of the wires is given as $r=d / 2=0.125 \mathrm{~cm}$ Unloaded length of the steel wire is given as $l_{1}=1.5 \mathrm{~m}$ Unloaded...
Read the following two statements below carefully and state, with reasons, if it is true or false.(a) The Young’s modulus of rubber is greater than that of steel;(b) The stretching of a coil is determined by its shear modulus.
(a) True. Stretching a coil does not affect its length; instead, it changes its shape, which requires shear modulus. (b) False. This is because rubber has more strain than steel for the same amount...
The stress-strain graphs for materials  and
and  are shown in the figure below.
are shown in the figure below.
(a) Which of the materials has the greater Young's modulus? (b) Which of the two is the stronger material? Solution: (a) We can observe from the graphs that for a given strain, $A$ has a higher...
Figure below shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strength for this material?
Solution: (a) Young's modulus, $Y=\frac{Stress}{Strain}$ $=150 \times 10^{6} / 0.002$ $=150 \times 10^{6} / 2 \times 10^{-3}$ $=75 \times 10^{9} \mathrm{Nm}^{-2}$ $=75 \times 10^{10}...
A steel wire of length 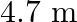 and cross-sectional area
and cross-sectional area 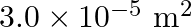 stretches by the same amount as a copper wire of length
stretches by the same amount as a copper wire of length 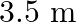 and cross-sectional area of
and cross-sectional area of 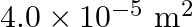 under a given load. What is the ratio of Young’s modulus of steel to that of copper?
under a given load. What is the ratio of Young’s modulus of steel to that of copper?
Length of the steel wire is given as $l_{1}=4.7 \mathrm{~m}$ Cross-sectional area of the steel wire is given as $a_{1}=3.0 \times 10^{-5} \mathrm{~m}^{2}$ Length of the copper wire is given as...
One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards the centre) is : (i) T (ii) T – mv2/l (iii) T + mv2/l (iv) 0 T is the tension in the string. [Choose the correct alternative].
T is the particle's net force, and it is directed towards the centre. It gives the particle the centrifugal force it needs to travel in a circle.
A train runs along an unbanked circular track of radius of 30 m at a speed of 54 km/h. The mass of the train is 106 kg. What provides the centripetal force required for this purpose the engine or the rails? What is the angle of banking required to prevent wearing out of the rail?
The track's radius is 30 metres. The train's speed = 54 km/h = 54 x (5/18) = 15 m/s The train's mass is 106 kg. The force of lateral friction created by the rails on the train wheels provides the...
Figure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 ms-2. What is the net force on the man? If the coefficient of static friction, between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man = 65 kg.)
Here, the conveyor belt's acceleration is a = 1 ms-2. s=0.2 is the static friction coefficient. m = 65 kg m = 65 kg m = 65 kg m = 65 kg m = 65 kg Ma = 65 x 1 = 65N is the Net Force. The friction...
Figure shows the position-time graph of a particle of mass 0.04 kg. Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the particle? What is the magnitude of each impulse?
This graph might represent a ball rebounding between two walls separated by two centimetres. Every two seconds, the ball bounces back and forth between the walls at a constant pace. 2 x 10-2)/2 =...
Explain why a cricketer moves his hands backwards while holding a catch.
The ball will have a lot of momentum when the batsman smashes it. When he slides his hands rearward, the contact duration increases, and the force decreases.
Explain why passengers are thrown forward from their seats when a speeding bus stops suddenly,
Because of the inertia of motion. When a bus abruptly stops, the bottom half of a person's body in touch with the seat comes to a halt, while the upper part of the body continues to move. As a...
Explain why a horse cannot pull a cart and run in empty space,
When the horse pulls the cart, it exerts a certain amount of force on the ground. The ground will exert an equal and opposite reaction force on the horse's feet if the third rule of motion is...
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev./min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
The stone weighs 0.25 kilogramme. r = 1.5 m Radius n= 40/60 = (23) rev/sec is the number of revolutions per second. = 2n = 2 x 3.14 x (23) is the angular velocity. The centripetal force is provided...
A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)
The ball's speed is 54 km/h. The ball is deflected backwards to a total angle of 450 degrees. The initial momentum of the ball is mucosӨ = (0.15 x 54 x 1000 x cos 22. 5)/3600 = 0.15 x 15 x 0.9239...
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a tight string. A horizontal force F = 600 N is applied to (i) A, (ii) B along the direction of string. What is the tension in the string in each case?
Given, A body mass of 10 kilogrames (m1) B, m2 = 20 kg, 600 N horizontal force m = m1 + m2 = 30 kg is the total mass of the system. Using Newton's second rule of motion, we can calculate ma = f...
Figure shows the position-time graph of a particle of mass 4 kg. What is the (a) force on the particle for t 4 s, 0 < t < 4 s? (b) impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only).
When t<0, the particle's distance travelled is zero. As a result, the particle's force is zero. When 0< t< 4s occurs, the particle is travelling at a constant speed. As a result, there will...
. A man of mass 70 kg, stands on a weighing machine in a lift, which is moving (a) upwards with a uniform speed of 10 ms-1. (b) downwards with a uniform acceleration of 5 ms-2. (c) upwards with a uniform acceleration of 5 ms-2. What would be the readings on the scale in each case? (d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
m = 70 kg 10 m/s2 = g In each scenario, the weighing machine measures the response R, or apparent weight. (a) The lift's acceleration equals 0 when it travels upwards at a uniform speed of 10 m/s. R...
A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is 1 ms-1. What is the trajectory of the bob if the string is cut when the bob is at one of its extreme positions?
(a) The velocity of the bob is zero when it is at one of its extreme positions. If the string is severed, the bob will fall vertically downward due to its weight F = mg.
A truck starts from rest and accelerates uniformly at 2.0 ms-2. At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the (a) velocity, and (b) acceleration of the stone at t = 11s? (Neglect air resistance.)
u = 0 is the initial velocity. a = 2 ms-2, a = 2 ms-2, a = 2 ms-2, a = 2 m t=10s t=10s t=10s t=10 We get v = u + at using the equation v = u + at. 20 m/s = v = 0 + 2 x 10 ...
A body of mass 0.40 kg moving initially with a constant speed of 10 ms-1 to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be t = 0, the position of the body at that time to be x = 0, and predict its position at t = -5 s, 25 s, 100 s.
Given, Body mass is 0.40 kg. u = 10 m/s initial velocity f = -8 N force (retarding force) Using the formula S = ut + (12) at2, (a) At time t = – 5 s, position From t = 0 s, the force acts on the...
The driver of a three-wheeler moving at a speed of 36 km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. What is the average retarding force on the vehicle? The mass of the three-wheeler is 400 kg, and the mass of the driver is 65 kg.
Given, u=36 km/h is the initial velocity. v = 0 is the final velocity. The three-mass wheeler's is m1=400 kg. The driver's mass is m2 = 65 kg. The time it took to bring the car to a complete stop...
. A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m s-1. How long does the body take to stop?
Here, – 50 N force (since it is a retarding force) m = 20 kg mass 0 = v u = 15 m s-1 u = 15 m s-1 u = 15 m F = ma force a = F/m = -50/20 = – 2.5 ms-2 v = u + at is the equation to use. 0 = 15 + (-...
Give the magnitude and direction of the net force acting on a stone of mass 0.1 kg, (a) just after it is dropped from the window of a stationary train (b) just after it is dropped from the window of a train running at a constant velocity of 36 km/h (c ) just after it is dropped from the window of a train accelerating with1 m s-2 (d) lying on the floor of a train which is accelerating with 1 m s-2, the stone being at rest relative to the train. Neglect air resistance throughout.
(a) Stone mass = 0.1 kg 10 ms^(-2)= acceleration F = mg = 0.1 x 10 = 1.0 N is the net force. The force is applied vertically and downwards. (b) The train maintains a steady...
Which of the following does not describe the elastic collision of two billiard balls? Distance between the centres of the balls is r.
(i), (ii), (iii), (iv) and (vi). The distance between two masses in a system is inversely proportional to their potential energy. As the two balls grow closer to each other, the potential energy of...
On a frictionless track, a trolley moves with a speed of 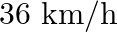 with a mass of
with a mass of 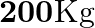 . A child whose mass is 20 kg runs on the trolley with a speed of
. A child whose mass is 20 kg runs on the trolley with a speed of 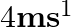 from one end to other which is
from one end to other which is 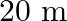 . The speed is relative to the trolley in the direction opposite to its motion. Find the final speed of the trolley and the distance the trolley moved from the time the child began to run.
. The speed is relative to the trolley in the direction opposite to its motion. Find the final speed of the trolley and the distance the trolley moved from the time the child began to run.
Mass is given as $m=200 \mathrm{Kg}$ Speed is given as $v=36 \mathrm{~km} / \mathrm{h}=10 \mathrm{~m} / \mathrm{s}$ Mass of boy is given as $=20 \mathrm{Kg}$ Initial momentum will be, $(M+m) v$...
A bolt of mass 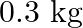 falls from the ceiling of an elevator moving down with a uniform speed of
falls from the ceiling of an elevator moving down with a uniform speed of 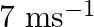 . It hits the floor of the elevator (length of elevator
. It hits the floor of the elevator (length of elevator 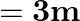 ) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?
) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?
Mass of the bolt is given as $m=0.3 \mathrm{~kg}$ Potential energy of the bolt is given as $m g h=0.3 \times 9.8 \times 3=8.82\rfloor$ The bolt does not return to its original position. As a result,...
A 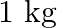 block situated on a rough incline is connected to a spring of spring constant 100
block situated on a rough incline is connected to a spring of spring constant 100 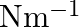 as shown in Fig. The block is released from rest with the spring in the unstretched position. The block moves
as shown in Fig. The block is released from rest with the spring in the unstretched position. The block moves 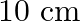 down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
Solution: Spring constant is given as $\mathrm{k}=100 \mathrm{~N} \mathrm{~m}^{m}$ Displacement in the block is given as $\mathrm{x}=10 \mathrm{~cm}=0.1 \mathrm{~m}$ At equilibrium: Normal reaction...
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track Fig. Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given 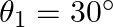 ,
, 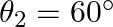 , and
, and 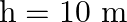 , what are the speeds and times taken by the two stones?
, what are the speeds and times taken by the two stones?
Solution: The sides $A B$ and $A C$ of the figure are both inclined to the horizontal at $\theta_{1}$ and $\theta_{2}$, respectively. According to the law of mechanical energy conservation,...
A bullet of mass 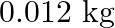 and horizontal speed
and horizontal speed 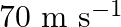 strikes a block of wood of mass
strikes a block of wood of mass 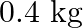 and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Mass of the bullet is given as $m_{1}=0.012 \mathrm{~kg}$ Initial speed of the bullet is given as $u_{1}=70 \mathrm{~m} / \mathrm{s}$ Mass of the wooden block is given as $m_{2}=0.4 \mathrm{~kg}$...
A family uses 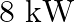 of power. (a) Direct solar energy is incident on the horizontal surface at an average rate of
of power. (a) Direct solar energy is incident on the horizontal surface at an average rate of 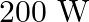 per square meter. If
per square meter. If 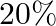 of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?(b) Compare this area to that of the roof of a typical house.
of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?(b) Compare this area to that of the roof of a typical house.
(a) Power used by family is given as $p=8 \mathrm{KW}=8000 \mathrm{~W}$ Solar energy received per square metre is given as $200 \mathrm{~W} / \mathrm{m}^{2}$ Percentage of energy converted to useful...
A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 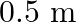 each time. Assume that the potential energy lost each time she lowers the mass is dissipated. (a) How much work does she do against the gravitational force? (b) Fat supplies
each time. Assume that the potential energy lost each time she lowers the mass is dissipated. (a) How much work does she do against the gravitational force? (b) Fat supplies 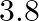
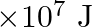 of energy per kilogram which is converted to mechanical energy with a
of energy per kilogram which is converted to mechanical energy with a 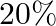 efficiency rate. How much fat will the dieter use up?
efficiency rate. How much fat will the dieter use up?
Mass is given as $\mathrm{m}=10 \mathrm{~kg}$ Height to which the mass is lifted is given as $h=0.5 \mathrm{~m}$ Number of times is hiven as $n=1000$ (a) Work done against gravitational force can be...
The windmill sweeps a circle of area A with their blades. If the velocity of the wind is perpendicular to the circle, find the air passing through it in time 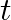 and also the kinetic energy of the air.
and also the kinetic energy of the air. 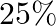 of the wind energy is converted into electrical energy and
of the wind energy is converted into electrical energy and 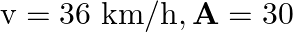
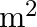 and the density of the air is
and the density of the air is 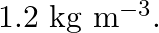 What is the electrical power produced?
What is the electrical power produced?
Area = A Velocity $=\mathrm{V}$ Density $=\rho$ (a) Volume of the wind through the windmill per sec is given by $=\mathrm{Av}$ Mass is given by $=\rho \mathrm{AV}$ So, Mass $m$ through the windmill...
A body of mass 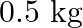 travels in a straight line with velocity
travels in a straight line with velocity 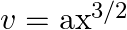 where
where 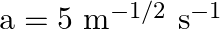 . What is the work done by the net force during its displacement from
. What is the work done by the net force during its displacement from 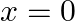 to
to 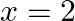 m?
m?
Let the mass of the body be $m$ $m=0.5 \mathrm{~kg}$ Velocity of the body is represented by $v=a x^{3 / 2}$ where, $a=5 \mathrm{~m}^{-1 / 2} \mathrm{~s}^{-1}$. Initial velocity at $x=0$ will be...
A trolley of mass 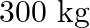 carrying a sandbag of
carrying a sandbag of 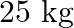 is moving uniformly with a speed of
is moving uniformly with a speed of 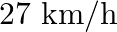 on a frictionless track. After a while, the sand starts leaking out of a hole on the floor of the trolley at the rate of
on a frictionless track. After a while, the sand starts leaking out of a hole on the floor of the trolley at the rate of 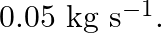 What is the speed of the trolley after the entire sandbag is empty?
What is the speed of the trolley after the entire sandbag is empty?
The sandbag is placed in the trolley, which travels at a constant speed of 27 km/h. There is no system that acts as an external force. There will be no external force operating on the system even if...
The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 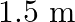 , what is the speed with which the bob arrives at the lowermost point, given that it dissipated
, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 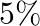 of its initial energy against air resistance?
of its initial energy against air resistance?
Length of the pendulum is given as $\mid=1.5 \mathrm{~m}$ Potential of the bob at the horizontal position is given as $=m g h=m g \mid$ When the bob goes from the horizontal position to the lowest...
A ball A which is at an angle 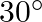 to the vertical is released and it hits a ball B of same mass which is at rest. Does the ball A rises after collision? The collision is an elastic collision.
to the vertical is released and it hits a ball B of same mass which is at rest. Does the ball A rises after collision? The collision is an elastic collision.
When the ball A collides with the stationary ball B in an elastic collision, the ball B gains the velocity of the ball A, while the ball A comes to a stop immediately after the collision....
Two identical ball bearings in contact with each other and resting on a frictionless table is hit head-on by another ball bearing of the same mass moving initially with a speed 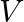 . If the collision is elastic, which of the following figure is a possible result after collision?
. If the collision is elastic, which of the following figure is a possible result after collision?
Solution: The mass of the ball bearing is given as $\mathrm{m}$ Before the collision, Total Kinetic Energy of the system will be $=1 / 2 m v^{2}+0=1 / 2 m v^{2}$ After the collision, Total Kinetic...
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble, (a) during its upward motion (b) during its downward motion (c) at the highest point where it is momentarily at rest. Do your Solutions change if the pebble was thrown at an angle of 45° with the horizontal direction? Ignore air resistance
(a) The acceleration due to gravity acts downwards throughout the upward motion of the pebble, thus the magnitude of the force on the pebble is 0.5 N = F = mg = 0.05 kg x 10 ms-2 The force is in a...
1. Give the magnitude and direction of the net force acting on (a) a drop of rain falling down with a constant speed (b) a cork of mass 10 g floating on water (c) a kite skillfully held stationary in the sky (d) a car moving with a constant velocity of 30 km/h on a rough road (e) a high-speed electron in space far from all material objects, and free of electric and magnetic fields.
(a)The raindrop continues to fall at the same rate. As a result, the acceleration will be zero. Because F = ma, the force exerted on the drop will be zero when the acceleration is zero. (b) The cork...
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 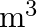 in
in 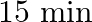 . If the tank is
. If the tank is 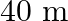 above the ground, and the efficiency of the pump is
above the ground, and the efficiency of the pump is 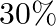 , how much electric power is consumed by the pump?
, how much electric power is consumed by the pump?
Volume of the tank is given as $30 \mathrm{~m}^{3}$ Time taken to fill the tank is given as $15 \mathrm{~min}=15 \times 60=900 \mathrm{~s}$ Height of the tank above the ground is given as $h=40...
A molecule in a gas container hits a horizontal wall with speed 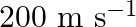 and angle
and angle 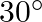 with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
For an elastic or inelastic collision, momentum is always preserved. The molecule approaches and rebounds with the same speed of $200 \mathrm{~m} / \mathrm{s}$. $u=v=200 \mathrm{~m}...
A raindrop of radius 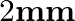 falls from a height of
falls from a height of 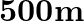 above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is
above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 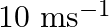 ?
?
Radius of the drop is given as $2 \mathrm{~mm}=2 \times 10^{-3} \mathrm{~m}$. Height from which the raindrops fall is given as $\mathrm{S}=500 \mathrm{~m}$. The density of water is given as...
An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 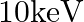 , and the second with
, and the second with 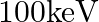 . Which is faster, the electron or the proton? Obtain the ratio of their speeds. (electron mass
. Which is faster, the electron or the proton? Obtain the ratio of their speeds. (electron mass  , proton mass
, proton mass 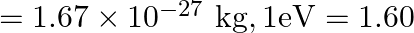
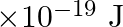 )
)
Electron mass is given as $m_{e}=9.11 \times 10^{-31} \mathrm{~kg}$ Proton mass is given as $m_{p}=1.67 \times 10^{-27} \mathrm{~kg}$ Electron's kinetic energy can be calculated as...
A body constrained to move along the z-axis of a coordinate system is subject to a constant force  given by
given by  where i,
where i, 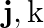 , are unit vectors along the
, are unit vectors along the  – and
– and 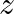 -axis of the system respectively. What is the work done by this force in moving the body at a distance of
-axis of the system respectively. What is the work done by this force in moving the body at a distance of 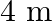 along the z-axis?
along the z-axis?
The body is displaced by $4 \mathrm{~m}$ along $z$-axis, so we have, $\vec{S}=0 \hat{i}+0 \hat{j}+4 \hat{k}$ $\vec{F}=-\hat{i}+2 \hat{j}+3 \hat{k}$ Work done can be calculated as, $W=\vec{F} \cdot...
A body is moving unidirectionally under the influence of a source of constant power. Its dis placement in time t is proportional to
(i) 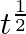
(ii) 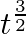
(iii) 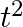
(iv) 
Power is given by, $P=F V$ $=\operatorname{mav}=\operatorname{mv} \frac{d v}{d t}$ vdv $=\frac{k}{m} \mathrm{dt}$ On integration, we get, 10 $\frac{v^{2}}{2}=\frac{k}{m} d t$...
A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time  is proportional to
is proportional to
(i) 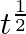
(ii) 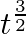
(iii) 
(iv) 
Let the body mass be $m$ Let the Acceleration be $a$ According to Newton's second law of motion, we have, $F=m a($ constant $)$ As, $\mathrm{a}=\frac{d v}{d t}=$ constant $d v=d t \times$ constant...
Answer carefully, with reasons :
(a) In an inelastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an inelastic collision of two balls?
(b) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during a collision, not gravitational potential energy).
(a) In an inelastic collision, there will be a loss of kinetic energy. After a collision, the K.E is always lower than the K.E before the impact. In an inelastic collision, the system's total linear...
Answer carefully, with reasons :
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?
(a) In an elastic collision, the initial and ultimate kinetic energy are equal. There is no kinetic energy conservation when the two balls contact. It is transformed into kinetic energy. (b) In an...
State if each of the following statements is true or false. Give reasons for your answer
(a) Work done in the motion of a body over a closed loop is zero for every force in nature.
(b) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
(a) False. The work done by the conservative force on the moving body in a closed loop is zero. (b) True
State if each of the following statements is true or false. Give reasons for your answer
(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.
(b) The total energy of a system is always conserved, no matter what internal and external forces on the body are present.
(a) False Both bodies' momentum and energy are conserved collectively, rather than separately. (b) False. External forces on the system have the ability to work on the body and modify the system's...
Underline the correct alternative:
(a) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system
(b) In an inelastic collision of two bodies, the quantities which do not change after the collision is the total kinetic energy/total linear momentum/total energy of the system of two bodies.
(a) External force Internal forces, regardless of their direction, cannot cause a change in momentum. As a result, the change in total momentum is proportional to the system's external force. (b)...
Underline the correct alternative:
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
(a) Decreases When a body is displaced in the direction of the force, the conservative force does positive work on it, causing the body to migrate to the center of force. As a result, the distance...
Answer the following:
(a) An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?(b) In the Figure, the man walks 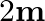 carrying a mass of
carrying a mass of 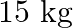 on his hands. In Fig., he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of
on his hands. In Fig., he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 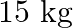 hangs at its other end. In which case is the work done greater?
hangs at its other end. In which case is the work done greater?
Solution: (a) As the satellite approaches the Earth, its potential energy drops, and since the system's total energy should remain constant, the kinetic energy increases. As a result, the...
Answer the following:
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(a) The mass of the rocket is lowered when the shell burns up owing to friction. As per the law of conservation of energy, we have, Total energy $=$ kinetic energy $+$ potential energy $=m g...
The potential energy function for a particle executing linear simple harmonic motion is given by 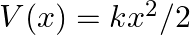 , where
, where  is the force constant of the oscillator. For
is the force constant of the oscillator. For 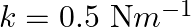 , the graph of
, the graph of 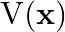 versus
versus  is shown in Figure. Show that a particle of total energy
is shown in Figure. Show that a particle of total energy 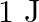 moving under this potential must ‘turn back’ when it reaches
moving under this potential must ‘turn back’ when it reaches 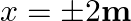 .
.
Solution: Energy of the particle will be, $\mathrm{E}=1 \mathrm{~J}$ $\mathrm{K}=0.5 \mathrm{~N} \mathrm{~m}^{-1}$ $\mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{mv}^{2}$ Based on law of conservation...
Given in Figure, are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
(a) (b) The total energy is given by the relation, $E=K . E .+P . E$. So, $K_{. E}=E-P . E .$ There can never be a negative amount of kinetic energy. In the region where K.E. becomes negative, the...
Given in Figure, are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
The total energy is given by the relation, $E=K . E .+P . E$. So, $K_{. E}=E-P . E .$ There can never be a negative amount of kinetic energy. In the region where K.E. becomes negative, the particle...
A body of mass 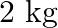 initially at rest moves under the action of an applied horizontal force of
initially at rest moves under the action of an applied horizontal force of 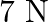 on a table with the coefficient of kinetic friction
on a table with the coefficient of kinetic friction 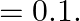 Compute the
Compute the
(a) work done by the net force on the body in 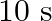 ,
,
(b) change in kinetic energy of the body in 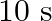 .
.
Mass of the body is given as $2 \mathrm{~kg}$ Horizontal force applied is given as $7 \mathrm{~N}$ Coefficient of kinetic friction is given as $0.1$ Acceleration produced by the applied force can be...
A body of mass 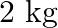 initially at rest moves under the action of an applied horizontal force of
initially at rest moves under the action of an applied horizontal force of 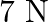 on a table with the coefficient of kinetic friction
on a table with the coefficient of kinetic friction 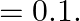 Compute the
Compute the
(a) work done by the applied force in 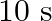 ,
,
(b) work done by friction in 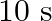
Mass of the body is given as $2 \mathrm{~kg}$ Horizontal force applied is given as $7 \mathrm{~N}$ Coefficient of kinetic friction is given as $0.1$ Acceleration produced by the applied force can be...
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Work completed is negative. It is noticed that the bob's orientation and the air resistance acting on it are in different directions.
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by friction on a body sliding down an inclined plane,
(b) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity
(a) The direction of motion of the object is opposite the direction of the frictional force, as can be seen. As a result, the work completed is negative. (b) The frictional force acting on an object...
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) work done by the gravitational force in the above case
(a) Work done is positive. It is obvious that both the force and the displacement are in the same direction. (b) It should be observed that the object's displacement is upward, but the force of...
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(i) Show 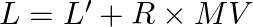 where
where 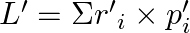 is the angular momentum of the system about the centre of mass with velocities considered with respect to the centre of mass. Note
is the angular momentum of the system about the centre of mass with velocities considered with respect to the centre of mass. Note 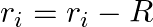 , rest of the notation is the standard notation used in the lesson. Note L’ and MR
, rest of the notation is the standard notation used in the lesson. Note L’ and MR 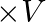 can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(ii) Prove that : 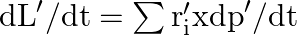 Further prove that:
Further prove that: 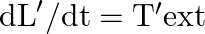 Where t’ext is the sum of all external torques acting on the system about the centre of mass. (Clue : A pply Newton’s Third Law and the definition of centre of mass. Consider that internal forces between any two particles act along the line connecting the particles.)
Where t’ext is the sum of all external torques acting on the system about the centre of mass. (Clue : A pply Newton’s Third Law and the definition of centre of mass. Consider that internal forces between any two particles act along the line connecting the particles.)
Here $\vec{r}_{i}=\vec{r}_{i}+\vec{R}+R \ldots$ (1) also, $\vec{V}_{i}=\vec{V}_{i}+\vec{V} \ldots \ldots .$ (2) Where $\vec{r}_{i}^{\overrightarrow{3}}$ and $\vec{v}_{i}^{\overrightarrow{3}}$ denote...
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
 Show
Show  Where
Where  is the momentum of the
is the momentum of the 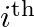 particle (of mass
particle (of mass 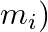 and
and 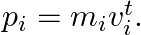 Note
Note 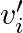 is the velocity of the
is the velocity of the 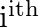 particle with respect to the centre of mass.Also, verify using the definition of the centre of mass that
particle with respect to the centre of mass.Also, verify using the definition of the centre of mass that 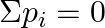
(ii) Prove that 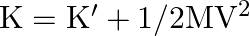 Where
Where  is the total kinetic energy of the system of particles,
is the total kinetic energy of the system of particles, 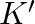 is the total kinetic energy of the system when the particle velocities are taken relative to the center of mass and
is the total kinetic energy of the system when the particle velocities are taken relative to the center of mass and 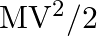 is the kinetic energy of the translation of the system as a whole.
is the kinetic energy of the translation of the system as a whole.
i)Here $\vec{r}_{i}=\vec{r}_{i}+\vec{R}+R \ldots$ also, $\vec{V}_{i}=\vec{V}_{i}+\vec{V} \ldots \ldots .$ Where $\vec{r}_{i}^{\overrightarrow{3}}$ and $\vec{v}_{i}^{\overrightarrow{3}}$ denote the...
Read the statement below carefully, and state, with reasons, if it is true or false; A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
True. Rolling happens only when there is a frictional force to provide the torque; otherwise, the wheel merely slips down the plane on its own weight.
Read each statement below carefully, and state, with reasons, if it is true or false;
(a) The instantaneous acceleration of the point of contact during rolling is zero.
(b) For perfect rolling motion, work done against friction is zero.
(a) False. The instantaneous acceleration of a rolling object will have a value that is not zero. (b) True. Because the frictional force is zero during perfect rolling, no work is done against it.
Read each statement below carefully, and state, with reasons, if it is true or false;
(a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
(b) The instantaneous speed of the point of contact during rolling is zero.
(a) False. The direction of frictional force is the polar opposite of the centre of mass's motion. Because the centre of mass of a rolling object moves backwards, the frictional force acts in the...
A cylinder of mass 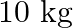 and radius
and radius 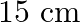 is rolling perfectly on a plane of inclination
is rolling perfectly on a plane of inclination 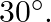 The coefficient of static friction
The coefficient of static friction 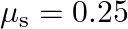 . If the inclination
. If the inclination  of the plane is increased, at what value of
of the plane is increased, at what value of  does the cylinder begin to skid, and not roll perfectly?
does the cylinder begin to skid, and not roll perfectly?
The given situation can be depicted as: Mass is given as $m=10 \mathrm{~kg}$ Radius is given as $r=15 \mathrm{~cm}=0.15 \mathrm{~m}$ Co-efficient of kinetic friction is given as $\mu_{s}=0.25$ Angle...
A cylinder of mass 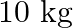 and radius
and radius 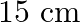 is rolling perfectly on a plane of inclination
is rolling perfectly on a plane of inclination 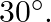 The coefficient of static friction
The coefficient of static friction 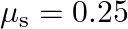
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
The above situation can be depicted as: Mass is given as $m=10 \mathrm{~kg}$ Radius is given as $r=15 \mathrm{~cm}=0.15 \mathrm{~m}$ Co-efficient of kinetic friction is given as $\mu_{s}=0.25$ Angle...
A solid disc and a ring, both of radius 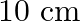 are placed on a horizontal table simultaneously, with an initial angular speed equal to
are placed on a horizontal table simultaneously, with an initial angular speed equal to 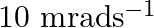 . Which of the two will start to roll earlier? The coefficient of kinetic friction is
. Which of the two will start to roll earlier? The coefficient of kinetic friction is 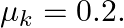
The radius of the ring and the disc is given as r = 10 cm = 0.10 m Initial angular speed is given as ω0 =10 π rad s–1 The coefficient of kinetic friction is given as μk = 0.2 According to Newton’s...
A disc rotating about its axis with angular speed  is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points
is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points 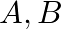 and
and  on the disc shown in Figure. Will the disc roll in the direction indicated?
on the disc shown in Figure. Will the disc roll in the direction indicated?
Solution: The respective linear velocities are : For point $A, v_{A}=r \omega_{0}$ For point $B, v_{B}=r \omega_{0}$ both in the direction of arrow For point $C, v_{c}=(R / 2) \omega_{0}$ in the...
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height 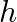 is given by
is given by 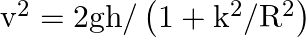 using dynamical consideration (i.e. by consideration of forces and torques). Note
using dynamical consideration (i.e. by consideration of forces and torques). Note 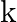 is the radius of gyration of the body about its symmetry axis, and
is the radius of gyration of the body about its symmetry axis, and  is the radius of the body. The body starts from rest at the top of the plane.
is the radius of the body. The body starts from rest at the top of the plane.
The given question can be represented as: where, $R$ is the body's radius $g$ is the acceleration due to gravity $\mathrm{K}$ is the body's radius of gyration $v$ is the body's translational...
(a) Prove the theorem of perpendicular axes. (Hint: Square of the distance of a point 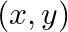 in the
in the  plane from an axis through the origin and perpendicular to the plane is
plane from an axis through the origin and perpendicular to the plane is 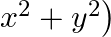 .
.
(b) Prove the theorem of parallel axes. (Hint: If the centre of mass of a system of n particles is chosen to be the origin 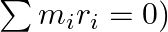 .
.
(a) The moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in...
Two discs of moments of inertia 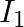 and
and 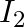 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds
about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds 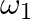 and
and 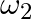 are brought into contact face to face with their axes of rotation coincident.
are brought into contact face to face with their axes of rotation coincident.
(a) What is the angular speed of the two-disc system?
(b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take 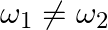
(a) Let I1 and I2 be the moment of inertia of the two turntables respectively. Let ω1 and ω2 be the angular speed of the two turntables respectively. So, we can say, Angular momentum of turntable...
A bullet of mass  and speed
and speed  is fired into a door and gets embedded exactly at the centre of the door. The door is
is fired into a door and gets embedded exactly at the centre of the door. The door is  wide and weighs
wide and weighs 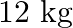 . It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
Velocity is given as v = 500 m/s Mass of bullet is given as m = 10 g or 10 × 10–3 kg The width of the door is given as L = 1 m The radius of the door is given as r = 1 / 2 Mass of the door is given...
A man stands on a rotating platform, with his arms stretched horizontally holding a 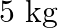 weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from
weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from 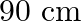 to
to 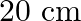 . The moment of inertia of the man together with the platform may be taken to be constant and equal to
. The moment of inertia of the man together with the platform may be taken to be constant and equal to 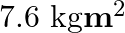 .
.
(a) What is his new angular speed? (Neglect friction.)
(b) Is kinetic energy conserved in the process? If not, from where does the change come about?
Mass of each weight is given as 5 kg The moment of inertia of the man-platform system is given as 7.6 kg m2 So, the moment of inertia when his arms are fully stretched to 90 cm can be calculated as,...
As shown in Figure the two sides of a step ladder BA and CA are 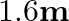 long and hinged at A. A rope DE,
long and hinged at A. A rope DE,  m is tied halfway up. A weight
m is tied halfway up. A weight 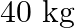 is suspended from a point F,
is suspended from a point F,  from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take
from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take 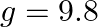
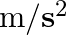 ) (Hint: Consider the equilibrium of each side of the ladder separately.)
) (Hint: Consider the equilibrium of each side of the ladder separately.)
Solution: The above figure can be redrawn as, where, $N_{B}$ is the force being applied by floor point $B$ on the ladder $N_{c}$ is the force being applied by floor point $C$ on the ladder The...
A solid cylinder rolls up an inclined plane of the angle of inclination 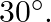 At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of
At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 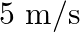 .
.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
initial velocity of the solid cylinder is given $v=5 \mathrm{~m} / \mathrm{s}$ Angle of inclination is given as $\theta=30^{\circ}$ We assume that the cylinder goes up to a height of $h$, so we get:...
The oxygen molecule has a mass of  and a moment of inertia of
and a moment of inertia of 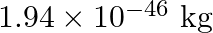
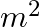 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is
about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 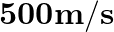 and that its kinetic energy of rotation is two-thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
and that its kinetic energy of rotation is two-thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Mass of one oxygen molecule is given as $m=5.30\times10^{-26}kg$ So, the mass of each oxygen atom will be $\frac{m}{2}$ Moment of inertia is given as $I=1.94\times10^{-46}kg m^{2}$ Velocity of the...
A hoop of radius 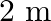 weighs
weighs 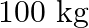 . It rolls along a horizontal floor so that its centre of mass has a speed of
. It rolls along a horizontal floor so that its centre of mass has a speed of 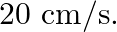 How much work has to be done to stop it?
How much work has to be done to stop it?
Radius of the ring is given as $r=2 \mathrm{~m}$ Mass of the ring s given as $m=100 \mathrm{~kg}$ Velocity of the hoop is given as $v=20 \mathrm{~cm} / \mathrm{s}=0.2 \mathrm{~m} / \mathrm{s}$ Total...
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
(a) Let m be the mass of the ball let h be the height of the ball let v be the final velocity of the ball at the bottom of the plane The ball possesses Potential energy $mgh$ at the top of the...
Explain why (d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel (e) A spinning cricket ball in air does not follow a parabolic trajectory
Answer : (d) This is due to the conservation of momentum principle. The vessel gains backward motion while the flowing fluid gains forward momentum. (e) If there had been no air, a spinning cricket...
Explain why (c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
Answer : (c) The needle size determines the flow velocity, while thumb pressure determines the pressure. Bernoulli's theorem states that P + 1/2pv2 = constant. The pressure P has a single power in...
Explain why (a) To keep a piece of paper horizontal, you should blow over, not under, it (b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
Answer : (a) When we blow over a piece of paper, the velocity of the air above it becomes greater than the velocity of the air below it. According to Bernoulli's theorem, as the K.E. of air above...
Fill in the blanks using the word(s) from the list appended with each statement:
(c) For solids with an elastic modulus of rigidity, the shearing force is proportional to … , while for fluids, it is proportional to … (shear strain/rate of shear strain) (d) For a fluid in a...
Fill in the blanks using the word(s) from the list appended with each statement: (a) The surface tension of liquids generally … with temperatures (increases/decreases) (b) The viscosity of gases … with temperature, whereas the viscosity of liquids … with temperature (increases/decreases)
Answer : (a) Decreases (b) increases; decreases
Explain why (c) Surface tension of a liquid is independent of the area of the surface (d) Water with detergent disolved in it should have small angles of contact. (e) A drop of liquid under no external forces is always spherical in shape
Answer : (c) Because of surface tension, a liquid will always try to obtain the smallest possible surface area. A liquid drop will always take the shape of a sphere under zero external pressures...
Explain why (a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute. (b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Answer : (a) Water molecules exhibit weak intermolecular interactions but are attracted to solids by a strong force. As a result, they flow out. Mercury molecules, on the other hand, have a stronger...
A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of a radius of 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Answer : According to the question, the speed of the cyclist is 27 km/h Or, 27 x (5/18) = 7.5 m/s And radius of the road is 80 m The braking and the centripetal acceleration cause the net...
A fighter plane flying horizontally at an altitude of 1.5 km with a speed of 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s-1 to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take g = 10 m s-2 ).
Answer : According to the question, speed of the fighter plane is 720 km/h or, 720 x (5/18) = 200 m/s Altitude of the plane is1.5 km and the velocity of the shell is 600 m/s From the diagram above,...
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.
Ans: According to the question, the bullet is fired at an angle of 30° And the bullet impacts the ground at a distance = 3km or 3000 m Exprsssion for the Horizontal range is : R = u2 sin2θ/g Upon...
The position of a particle is given by
\[r=3.0t\hat{i}-2.0{{t}^{2}}\hat{j}+4.0\hat{k}m\] Where t is in seconds and the coefficients have the proper units for r to be in meters. (a) Find the ‘v’ and ‘a’ of the particle? (b) What is the...
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is 30°, what is the speed of the aircraft?
Answer : According to the question, the aircraft is flying at a height = 3400 m Let A and B represent the positions of aircraft which make an angle ∠AOB = 300. OC is a perpendicular drawn on AB. OC...
Can we associate a vector with (i) a sphere (ii) the length of a wire bent into a loop (iii) a plane area Clarify for the same.
Answer - No, No, Yes (i) We can't identify a sphere's volume with a vector, but we can associate a sphere's area with an area vector. (ii) A vector cannot be associated with the length of a wire...
As a vector is having both direction and magnitude, then is it necessary that if anything is having direction and magnitude it is termed as a vector? The rotation of an object is defined by the angle of rotation about the axis and the direction of rotation of the axis. Will it be a rotation of a vector?
Answer - No and no A physical quantity that has both direction and magnitude is not always referred to as a vector. The current, for example, is a scalar quantity despite having direction and...
Does a vector have a location in space? Will it fluctuate with time? Can two equivalent vectors x and y at various locations in space fundamentally have indistinguishable physical effects? Give cases in support of your answer.
Ans: No, Yes and No. In space, a vector has no defined place. The reason for this is that when a vector displaces in such a way that its direction and magnitude do not change, it remains invariant....
Read each statement below carefully and state, with reasons and examples, if it is true or false: A scalar quantity is one that (a) is conserved in a process (b) can never take negative values (c) must be dimensionless
Answer : (a) False Energy is not preserved in inelastic collisions, despite being a scalar quantity. b) False The temperature, although being a scalar quantity, can have negative values. c) False...
