Find the slope and the equation of the line passing through the points: (a, b) and ( – a, b)
Find the slope and the equation of the line passing through the points: (5, 3) and ( – 5, – 3)
Find the slope and the equation of the line passing through the points: (i) (3, – 2) and ( – 5, – 7)
Find the equation of the line passing through the point P( – 3, 5) and perpendicular to the line passing through the points A(2, 5) and B( – 3, 6)
Find the equation of the line passing through the point P(4, – 5) and parallel to the line joining the points A(3, 7) and B( – 2, 4).
Find the equation of a line which cuts off intercept 5 on the x – axis and makes an angle of 600 with the positive direction of the x – axis.
Find the equation of a line
Find the equation of a line whose slope is 4 and which passes through the point (5, – 7)
Find the equation of a line which is equidistant from the lines x = – 2 and x = 6.
Answer : For the equation of line equidistant from both lines, we will find point through which line passes and is equidistant from both line. As any point lying on x = - 2 line is ( - 2, 0) and on...
Find the equation of a vertical line passing through the point ( – 5, 6).
Answer : Equation of line parallel to y - axis (vertical) is given by x = constant, as x - coordinate is constant for every point lying on line i.e. 6. So, the required equation of line is given as...
Find the equation of a horizontal line passing through the point (4, – 2).
Answer : Equation of line parallel to x - axis (horizontal) is y = constant, as y - coordinate of every point on the line parallel to x - axis is - 2 i.e. constant. Therefore equation of the line...
Find the equation of a line parallel to the x – axis and having intercept – 3 on the y – axis.
Answer: Equation of line parallel to x - axis is given by y = constant, as x - coordinate of every point on the line parallel to y - axis is - 3 i.e. constant. So, the required equation of line is y...
Find the equation of a line parallel to the x – axis at a distance of
(i) 4 units above it
(ii) 5 units below it
Answer : (i) Equation of line parallel to x - axis is given by y = constant, as the y - coordinate of every point on the line parallel to x - axis is 4,i.e. constant. Now the point lies above x -...
. A(1, 1), B(7, 3) and C(3, 6) are the vertices of a ΔABC. If D is the midpoint of BC and AL ⊥ BC, find the slopes of (i) AD and (ii) AL.
Show that the points A(0, 6), B(2, 1) and C(7, 3) are three corners of a square ABCD. Find (i) the slope of the diagonal BD and (ii) the coordinates of the fourth vertex D.
If θ is the angle between the diagonals of a parallelogram ABCD whose vertices are A(0, 2), B(2,-1), C(4,
If θ is the angle between the lines joining the points (0, 0) and B(2, 3), and the points C(2, -2) and D(3, 5), show that
If A(1, 2), B(-3, 2) and C(3, 2) be the vertices of a ΔABC, show that
Find the angle between the lines whose slopes are
Find the slope of the line which makes an angle of 300 with the positive direction of the y-axis, measured anticlockwise.
The vertices of a quadrilateral are A(-4, -2), B(2, 6), C(8, 5) and D(9, -7). Using slopes, show that the midpoints of the sides of the quad. ABCD from a parallelogram.
A line passes through the points A(4, -6) and B(-2, -5). Show that the line AB makes an obtuse angle with the x-axis.
If the points A(a, 0), B(0, b) and P(x, y) are collinear, using slopes, prove that
If the three points A(h, k), B(x1, y1) and C(x2, y2) lie on a line then show that (h – x1)(y2 – y1) = (k – y1)(x2 – x).
Using slopes show that the points A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3) taken in order, are the vertices of a rectangle.
Using slopes show that the points A(6, -1), B(5, 0) and C(2, 3) are collinear.
If A(2, -5), B(-2, 5), C(x, 3) and D(1, 1) be four points such that AB and CD are perpendicular to each other, find the value of x.
Show that the line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (3, -3) and (5, -9).
Show that the line through the points (5, 6) and (2, 3) is parallel to the line through the points (9, -2) and (6, -5)
If the slope of the line joining the points A(x, 2) and B(6, -8) is value of x.
Find the inclination of a line whose slope is
Find the slope of a line whose inclination is
(i) 30°
(ii) 120°
(iii) 135°
(iv) 90°
Find the slope of a line whose inclination is (i) 30°
(ii) 120°
(iii) 135°
(iv) 90°
In what ratio is the line segment joining the points A(-4, 2) and B(8, 3) divided by the y-axis? Also, find the point of intersection.
Find the ratio in which the x-axis cuts the join of the points A(4, 5) and B(- 10, -2). Also, find the point of intersection.
Find the coordinates of the point which divides the join of A(-5, 11) and B(4, -7) in the ratio 2 : 7.
Find the area of ΔABC, the midpoints of whose sides AB, BC and CA are D(3, -1), E(5, 3) and F(1, -3) respectively.
Find the area of the quadrilateral whose vertices are A(-4, 5), B(0, 7), C(5, -5) and D(-4, -2).
Find the value of k for which the points A(-2, 3), B(1, 2) and C(k, 0) are collinear
Show that the points A(-5, 1), B(5, 5) and C(10, 7) are collinear.
Find the area of ΔABC whose vertices are A(-3, -5), B(5, 2) and C(-9, -3).
If the points A (-2, -1), B(1, 0), C(x, 3) and D(1, y) are the vertices of a parallelogram, find the values of x and y.
Show that the points A(2, -1), B(3, 4), C(-2, 3) and D(-3, -2) are the vertices of a rhombus.
Show that A(1, -2), B(3, 6), C(5, 10) and D(3, 2) are the vertices of a parallelogram.
Show that A(3, 2), B(0, 5), C(-3, 2) and D(0, -1) are the vertices of a square.
Show that the points A(2, -2), B(8, 4), C(5, 7) and D(-1, 1) are the angular points of a rectangle.
Show that the points A(1, 1), B(-1, -1) and C(-√3, √3) are the vertices of an equilateral triangle each of whose sides is 22 units.
Show that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right-angled triangle.
Using the distance formula, show that the points A(3, -2), B(5, 2) and C(8,8) are collinear.
Find a point on the y-axis which is equidistant from A(-4, 3) and B(5, 2).
A is a point on the x-axis with abscissa -8 and B is a point on the y-axis with ordinate 15. Find the distance AB.
Find the distance between the points A(x1, y1) and B(x2, y2), when
(i)AB is parallel to the x-axis
(ii) AB is parallel to the y-axis.
Find a point on the x-axis which is equidistant from the points A(7, 6) and B(- 3, 4).
If a point P(x, y) is equidistant from the points A(6, -1) and B(2, 3), find the relation between x and y.
. Find the distance of the point P(6, -6) from the origin.
Find the distance between the points:
(i) A(2, -3) and B(-6, 3)
(ii) C(-1, -1) and D(8, 11)
(iii) P(-8, -3) and Q(-2, -5)
(iv) R(a + b, a – b) and S(a – b, a + b)
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5o and the prism is made of a material of refractive index 1.5, the angle of incidence is
a) 7.5o
b) 5o
c) 15o
d) 2.5o
Answer: a) 7.5o The distance between the refracting surfaces is negligible with thin prisms, thus the prism angle (A) is very small. Because A = r1 + r2, if A is tiny, both r1 and r2 will be little...
The velocity-displacement graph of a particle is shown in the figure. a) Write the relation between v and x. b) Obtain the relation between acceleration and displacement and plot it.
a) Consider the point P(x,v) at any time t on the graph such that angle ABO is θ such that tan θ = AQ/QP = (v0-v)/x = v0/x0 When the velocity decreases from v0 to zero during the displacement, the...
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building?
For a free fall at 9m, the horizontal distance covered by the man should be at least 10 m. u = 0 a = 10 m/s2 s = 9 m t = t s = ut + 1/2 at2 Substituting the values, we get t = √9/3 = 3/√5 sec The...
A ball is dropped and its displacement vs time graph is as shown in the figure where displacement x is from the ground and all quantities are positive upwards. a) Plot qualitatively velocity vs time graph b) Plot qualitatively acceleration vs time graph
a) At t=0 and v=0 , v-t graph is: b) At x = 0, a-t graph is:
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
V = v1 = ? U = 0 h = 45 m a = g t = t V = u + at v1 = 0 + gt v1 = gt Therefore, when the ball is thrown upward, v1 = -gt V = v2 u = 40 m/s a = g t = t V = u + at v2 = 40 – gt The relative velocity...
It is a common observation that rain clouds can be at about a kilometre altitude above the ground. a) If a rain drop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h b) A typical rain drop is about 4 mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground. c) Estimate the time required to flatten the drop. d) Rate of change of momentum is force. Estimate how much force such a drop would exert on you. e) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
a) Velocity attained by the rain drop which is falling freely through the height h is: v2 = u2 – 2g(-h) As u = 0 v = √2gh = 100√2 m/s = 510 km/h b) Diameter of the drop, d = 2r = 4 mm Radius of the...
A motor car moving at a speed of 72 km/h cannot come to a stop in less than 3 s while for a truck this time interval is 5 s. On a highway the car is behind the truck both moving at 72 km/h. The truck gives a signal that it is going to stop at emergency. At what distance the car should be from the truck so that it does not bump onto the truck. Human response time is 0.5 s.
For truck, u = 20 m/s v = 0 a = ? t = 5s v = u + at a = 4 m/s2 For car, t = 3 s u = 20 m/s v = 0 a = ac v = u + at ac = -20/3 m/s2 Let s be the distance between the car and the truck when the truck...
A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 – t); 0
a) For maximum velocity v(t) dv(t)/dt = 0 Substituting the value for v, we get t = 1.5 seconds b) For average velocity = total distance/time taken Average velocity = 3 m And the average velocity is...
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval. The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15m at t = 2s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
Let the speed of ball 1 = u1 = 2u m/s Then the speed of ball 2 = u2 = u m/s The height covered by ball 1 before coming to rest = h1 The height covered by ball 2 before coming to rest = h2 We know...
A bird is tossing between two cars moving towards each other on a straight road. One car has a speed of 18 m/h while the other has the speed of 27 km/h. The bird starts moving from first car towards the other and is moving with the speed of 36 km/h and when the two cars were separated by 36 km. What is the total distance covered by the bird? What is the total displacement of the bird?
The relative speed of the cars = 27 + 18 = 45 km/h When the two cars meet together, time t is given as t = distance between cars/relative speed of cars = 36/(27+18) t = 4/5 h Therefore, distance...
A particle executes the motion described by x(t) = x0 (1 – e-γt) where t ≥ 0, x0 > 0 a) Where does the particles start and with what velocity? b) Find maximum and minimum values of x(t), v(t), a(t). Show that x(t) and a(t) increase with time and v(t) decreases with time.
a) x(t) = x0 (1 – e-γt) v(t) = dx(t)/dt = +x0 γ e-γt a(t) = dv/dt = x0 γ2 e-γt v(0) = x0 γ b) x(t) is minimum at t = 0 since t = 0 and [x(t)]min = 0 x(t) is maximum at t = ∞ since t = ∞ and...
An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
The concept used in this question will be based on the behaviour of a spherical object when it is dropped through a viscous fluid. When a spherical body of radius r is dropped, it is first...
Give example of a motion where x>0, v<0, a>0 at a particular instant.
Let the motion be represented as: x(t) = A + Be– γ t Let A>B and γ >0 Velocity is x(t) = dx/dt = -Be– γ t Acceleration is a(t) = dx/dt = B γ 2e– γ t Therefore, it can be said that x(t) > 0,...
Give examples of a one-dimensional motion where a) the particle moving along positive x-direction comes to rest periodically and moves forward b) the particle moving along positive x-direction comes to rest periodically and moves backwardπ
When an equation has sine and cosine functions, the nature is periodic. a) When the particle is moving in positive x-direction, it is given as t > sin t When the displacement is as a function of...
A uniformly moving cricket ball is turned back by hitting it with a bat for a very short time interval. Show the variation of its acceleration with taking acceleration in the backward direction as positive.
The force which is generated by the bat is known as impulsive force. When the effect of gravity is ignored, it can be said that the ball moves with a uniform speed horizontally and returns back to...
Refer to the graphs below and match the following:
Graph Characteristics a) i) has v > 0 and a < 0 throughout b) ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0 c) iii) has a point with zero displacement for t...
A ball is bouncing elastically with a speed 1 m/s between walls of a railway compartment of size 10 m in a direction perpendicular to walls. The train is moving at a constant velocity of 10 m/s parallel to the direction of motion of the ball. As seen from the ground, a) the direction of motion of the ball changes every 10 seconds b) speed of ball changes every 10 seconds c) average speed of ball over any 20 seconds intervals is fixed d) the acceleration of ball is the same as from the train
The correct option is b) speed of ball changes every 10 seconds, c) average speed of ball over any 20 seconds intervals is fixed, and d) the acceleration of the ball is the same as from the train
A spring with one end attached to a mass and the other to a rigid support is stretched and released. a) magnitude of acceleration, when just released is maximum b) magnitude of acceleration, when at equilibrium position is maximum c) speed is maximum when mass is at equilibrium position d) magnitude of displacement is always maximum whenever speed is minimum
The correct answer is a) magnitude of acceleration, when just released is maximum and c) speed is maximum when mass is at equilibrium position
For the one-dimensional motion, describe by x = t – sint a) x(t)>0 for all t>0 b) v(t)>0 for all t>0 c) a(t)>0 for all t>0 d) v(t) lies between 0 and 2
The correct answer is a) x(t)>0 for all t>0 and d) v(t) lies between 0 and 2
A graph of x versus t is shown in the figure. Choose correct alternatives from below. a) the particle was released from rest at t=0 b) at B, the acceleration a>0 c) at C, the velocity and the acceleration vanish d) average velocity for the motion A and D is positive e) the speed at D exceeds that at E
The correct answer is a) the particle was released from rest at t=0, c) at C, the velocity and the acceleration vanish and e) the speed at D exceeds that at E
The variation of quantity A with quantity B, plotted in figure describes the motion of a particle in a straight line. a) quantity B may represent time b) quantity A is velocity if motion is uniform c) quantity A is displacement if motion is uniform d) quantity A is velocity if motion is uniformly accelerated
The correct answer is a) quantity B may represent time, c) quantity A is displacement if motion is uniform, and d) quantity A is velocity if motion is uniformly accelerated
At a metro station, a girl walks up a stationary escalator in time t1. If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be a) (t1 + t2)/2 b) t1t2/(t2 – t1) c) t1t2/(t2 + t1) d) t1 – t2
The correct answer is c) t1t2/(t2 + t1)
The displacement of a particle is given by x = (t-2)2 where x is in metres and t is seconds. The distance covered by the particle in first 4 seconds is a) 4 m b) 8 m c) 12 m d) 16 m
The correct answer is b) 8 m
A vehicle travels half the distance L with speed V1 and the other half with speed V2, then its average speed is a) (V1+V2)/2 b) (2V1+V2)/(V1+V2) c) (2V1V2)/(V1+V2) d) L(V1+V2)/V1V2
The correct answer is c) (2V1V2)/(V1+V2)
A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct? a) x<0, v<0, a>0 b) x>0, v<0, a<0 c) x>0, v<0, a>0 d) x>0, v>0, a<0
The correct answer is a) x<0, v<0, a<0 The value of x and v becomes negative as the lift is moving from the 8th floor to the 4th floor whereas acceleration is acting upwards and stays...
Among the four graphs, there is only one graph for which average velocity over the time interval (0,T) can vanish for a suitably chosen T. Which one is it?
The correct answer is (b)
What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
Solution: It is given that a cube with 2 units edge, one of whose vertices coincides with the origin and the 3 edges passing through the origin, coincides with the positive direction of the axes...
Choose the correct answer from the given four options indicated against each of the Exercises if the distance between the points 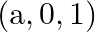 and
and 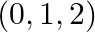 is
is 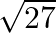 , then the value of
, then the value of 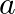 is
is
(A) 5
(B) 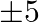
(C) 5
(D) none of these
Solution: Option(B) $\pm 5$ Explanation: Suppose $P$ be the point whose coordinate is $(a, 0,1)$ and $Q$ represents the point $(0,$, $(1,2) .$ It is given that, $\mathrm{PQ}=\sqrt{27}$ From the...
Choose the correct answer from the given four options indicated against each of the Exercises distance of the point 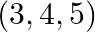 from the origin
from the origin 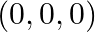 is
is
(A) 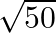
(B) 3
(C) 4
(D) 5
Solution: Option (A) $\sqrt{50}$ Explanation: Suppose $\mathrm{P}$ be the point whose coordinate is $(3,4,5)$ and $\mathrm{Q}$ represents the origin. From the distance formula it can be written as...
Choose the correct answer from the given four options indicated against each of the Exercises what is the length of foot of perpendicular drawn from the point 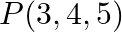 on
on  -axis
-axis
(A) 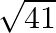
(B) 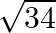
(C) 5
(D) none of these
Solution: Option(B) $\sqrt{34}$ Explanation: As it is known that $y$-axis lies on $x$ y plane and $y z$. Therefore, its distance from $x y$ and $y z$ plane is 0 . $\therefore$ By the basic...
Choose the correct answer from the given four options indicated against each of the Exercises the distance of point P (3, 4, 5) from the y z-plane is
(A) 3 units
(B) 4 units
(C) 5 units
(D) 550
Solution: (A) 3 units Explanation: From basic ideas of three-dimensional geometry, it is known that $x$-coordinate of a point is its distance from $y z$ plane. $\therefore$ The distance of Point $P...
Prove that the points (0, – 1, – 7), (2, 1, – 9) and (6, 5, – 13) are collinear. Find the ratio in which the first point divides the join of the other two.
Solution: It is given that the three points $A(0,-1,-7), B(2,1,-9)$ and $C(6,5,-13)$ are collinear So it can be written as $\begin{array}{l} A...
The mid-point of the sides of a triangle are (1, 5, – 1), (0, 4, – 2) and (2, 3, 4). Find its vertices. Also find the centroid of the triangle.
Solution: It is given that the mid-point of the sides of a triangle are $(1,5,-1),(0,4,-2)$ and $(2,3,$, 4). Suppose the vertices be $A\left(x_{1}, y_{1}, z_{1}\right), B\left(x_{2}, y_{2},...
Show that the three points 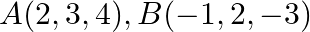 and
and 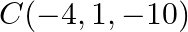 are collinear and find the ratio in which
are collinear and find the ratio in which  divides
divides 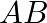 .
.
Solution: It is given that the three points are A $(2,3,4), \mathrm{B}(-1,2,-3)$ and $\mathrm{C}(-4,1,-10)$ We need to find collinear points, $\begin{array}{l}...
Let A 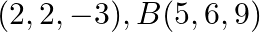 and C
and C 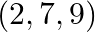 be the vertices of a triangle. The internal bisector of the angle
be the vertices of a triangle. The internal bisector of the angle  meets
meets 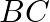 at the point
at the point 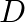 . Find the coordinates of
. Find the coordinates of 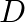 .
.
Solution: It is given $A(2,2,-3), B(5,6,9)$ and $C(2,7,9)$ are the vertices of a triangle. And it is also given that the internal bisector of the angle A meets BC at the point D....
If the origin is the centroid of a triangle ABC having vertices A (a, 1, 3), B (– 2, b, – 5) and C (4, 7, c), find the values of a, b, c.
Solution: It is given that the triangle ABC having vertices $A(a, 1,3), B(-2, b,-5)$ and $C(4,7, c)$ and origin is the centroid. The coordinates of the centroid for a triangle is given by the...
Find the coordinate of the points which trisect the line segment joining the points A 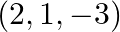 and
and 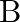
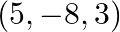
Solution: It is given the line segment joining the points are A $(2,1,-3)$ and $B(5,-8,3)$ Now suppose $P\left(x_{1}, y_{1}, z_{1}\right)$ and $Q\left(x_{2}, y_{2}, z_{2}\right)$ be the points which...
Three vertices of a Parallelogram ABCD are A (1, 2, 3), B (– 1, – 2, – 1) and C (2, 3, 2). Find the fourth vertex D.
Solution: It is given that the three consecutive vertices of a parallelogram ABCD are A $(1,2,3), B(-1,$, $-2,-1)$ and $C(2,3,2)$ Suppose the fourth vertex be $D(x, y, z)$. By using midpoint...
The mid-points of the sides of a triangle are (5, 7, 11), (0, 8, 5) and (2, 3, – 1). Find its vertices.
Solution: It is given that the mid-points of the sides of a triangle are $(5,7,11),(0,8,5)$ and $(2,3,-$ 1). Suppose the vertices be $A\left(x_{1}, y_{1}, z_{1}\right), B\left(x_{2}, y_{2},...
Find the centroid of a triangle, the mid-point of whose sides are 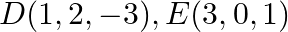 and
and 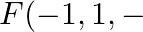 4).
4).
Solution: It is given that: Mid-points of sides of triangle $\mathrm{DEF}$ are: $\mathrm{D}(1,2,-3), \mathrm{E}(3,0,1)$ and $\mathrm{F}(-1,1,-4)$ Using the geometry of centroid, It is known that the...
Find the third vertex of triangle whose centroid is origin and two vertices are (2, 4, 6) and (0, –2, –5).
Solution: It is given the centroid is origin and two vertices are $(2,4,6)$ and $(0,-2,-5)$ Suppose the third vertex be $(x, y, z)$ The coordinates of the centroid for a triangle is given by the...
Show that the triangle 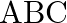 with vertices
with vertices 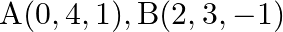 and
and 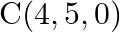 is right angled.
is right angled.
Solution: The given vertices are $A(0,4,1), B(2,3,-1)$ and $C(4,5,0)$ We need to prove right angled triangle, consider $\begin{array}{l}...
Three consecutive vertices of a parallelogram ABCD are A (6, – 2, 4), B (2, 4, – 8), C (–2, 2, 4). Find the coordinates of the fourth vertex.
Solution: The three consecutive vertices of a parallelogram $A B C D$ are as given $A(6,-2,4), B$ (2, $4,-8), C(-2,2,4)$ Suppose the forth vertex be $D(x, y, z)$ Midpoint of diagonal $A...
Show that the point 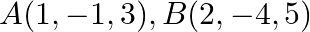 and
and 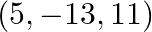 are collinear.
are collinear.
Solution: The given points are $A(1,-1,3), B(2,-4,5)$ and $(5,-13,11)$. We need to prove collinear, $\begin{array}{l} \mathrm{AB}=\sqrt{(1-2)^{2}+(-1+4)^{2}+(3-5)^{2}}=\sqrt{1+9+4}=\sqrt{14} \\...
Show that if 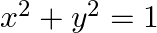 , then the point
, then the point 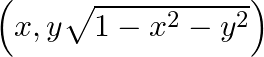 is at a distance 1 unit from the origin.
is at a distance 1 unit from the origin.
Solution: It is given that $x^{2}+y^{2}=1 \Rightarrow 1-x^{2}-y^{2}=0$ Distance of the point $\left(x, y \sqrt{1-x^{2}-y^{2}}\right)$ from origin is $=$ $\begin{array}{l}...
Find the distance from the origin to (6, 6, 7).
Solution: The distance from the origin to (6, 6, 7) $=\sqrt{{6^2}+{6^2}+{7^2}}$ $=\sqrt{{36}+{36}+{49}}$ $=\sqrt{121}$ $=11$ units
How far apart are the points (2, 0, 0) and (–3, 0, 0)?
Solution: The points $(2, 0, 0)$ and $(–3, 0, 0)$ are at a distance of $=$ $|2 − (−3)| = 5$ units.
Let A, B, C be the feet of perpendiculars from a point P on the xy, yz and zx planes respectively. Find the coordinates of A, B, C in each of the following where the point P is
(i) (4, – 3, – 5).
Solution: (i) $(4, – 3, – 5):- A (4, −3, 0), B (0, −3, −5), C (4, 0, −5)$
Let A, B, C be the feet of perpendiculars from a point P on the xy, yz and zx planes respectively. Find the coordinates of A, B, C in each of the following where the point P is
(i) (3, 4, 5)
(ii) (–5, 3, 7)
Solution: (i) $(3, 4, 5):- A (3, 4, 0), B (0, 4, 5), C (3, 0, 5)$ (ii) $(–5, 3, 7):- A (−5, 3, 0), B (0, 3, 7), C (−5, 0, 7)$
Let A, B, C be the feet of perpendiculars from a point P on the x, y, z-axis respectively. Find the coordinates of A, B and C in each of the following where the point P is :
(i) (4, – 3, – 5)
Solution: (i) $(4, – 3, – 5):- A (4, 0, 0), B (0, −3, 0), C (0, 0, −5)$
Let A, B, C be the feet of perpendiculars from a point P on the x, y, z-axis respectively. Find the coordinates of A, B and C in each of the following where the point P is :
(i) A = (3, 4, 2)
(ii) (–5, 3, 7)
Solution: (i) $(3, 4, 2):- A (3, 0, 0), B (0, 4, 0), C (0, 0, 2)$ (ii) $(–5, 3, 7):- A (−5, 0, 0), B (0, 3, 0), C (0, 0, 7)$
Name the octant in which each of the following points lies.
(i) (2, – 4, – 7)
(ii) (– 4, 2, – 5).
Solution: (i) $(2, – 4, – 7)$:- 8th Octant, (ii) $(– 4, 2, – 5)$:- 6th Octant.
Name the octant in which each of the following points lies.
(i) (– 4, 2, 5)
(ii) (–3, –1, 6)
Solution: (i) $(– 4, 2, 5)$:- 2nd Octant, (ii) $(–3, –1, 6)$:- 3rd Octant,
Name the octant in which each of the following points lies.
(i) (4, –2, –5)
(ii) (4, 2, –5)
Solution: (i) $(4, –2, –5)$:- 8th Octant, (ii) $(4, 2, –5)$:- 5th Octant,
Name the octant in which each of the following points lies.
(i) (1, 2, 3),
(ii) (4, – 2, 3),
Solution: (i) $(1, 2, 3)$:- 1st Octant, (ii) $(4, – 2, 3)$:- 4th Octant,
Locate the following points:
(i) (– 2, – 4, –7)
(ii) (– 4, 2, – 5).
Solution: (i) $(– 2, – 4, –7)$:- 7th octant, (ii) $(– 4, 2, – 5)$:- 6th octant.
Locate the following points:
(i) (1, – 1, 3),
(ii) (– 1, 2, 4)
Solution: (i) $(1, – 1, 3)$:- 4th octant, (ii) $(– 1, 2, 4)$:- 2nd octant,
Arrange them in a sequential manner, starting from the center – phellem, phellogen, phelloderm.
Solution: Phelloderm → Phellogen → Phellem Phellem or cork is the outermost layer, followed by phellogen (cork cambium) which in turn is followed by phelloderm.
Find the vector equation of the line passing through the point (1,2,-4) and perpendicular to the two lines: 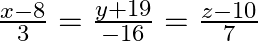 and
and 
Solution: The vector eq. of a line passing through a point with position vector $\vec{a}$ and parallel to a vector $\overrightarrow{\mathrm{b}}$ is...
If 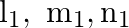 and
and 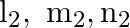 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are
are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are 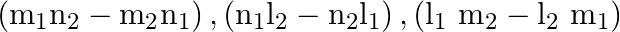
Solution: Let's consider $l, m, n$ be the direction cosines of the line perpendicular to each of the given lines. Therefore, $ll_{1}+m m_{1}+n n_{1}=0 \ldots(1)$ And...
In the following cases, find the distance of each of the given points from the corresponding given plane. Point Plane
(a) (0, 0, 0) 3x – 4y + 12 z = 3
(b) (3, -2, 1) 2x – y + 2z + 3 = 0
Solution: (a) The distance of the point $(0,0,0)$ from the plane $3 x-4 y+12=3 \Rightarrow$ $3 x-4 y+12 z-3=0$ is $\begin{array}{l} \frac{\left|a x_{1}+b y_{1}+c...
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Solution: (a) $7 x+5 y+6 z+30=0$ and $3 x-y-10 z+4=0$ It is given that The eq. of the given planes are $7 x+5 y+6 z+30=0$ and $3 x-y-10 z+4=0$ Two planes are $\perp$ if the direction ratio of the...
Find the angle between the planes whose vector equations are 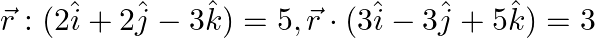
Solution: It is given that The eq. of the given planes are $\vec{r}(2 \hat{i}+2 \hat{j}-3 \hat{k})=5 \text { and } \vec{r}(3 \hat{i}-3 \hat{j}+5 \hat{k})=5$ If $\mathrm{n}_{1}$ and $\mathrm{n}_{2}$...
Find the vector equation of the plane passing through the intersection of the planes 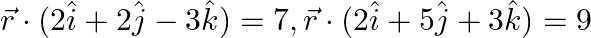 and through the point
and through the point 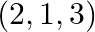
Solution: Let's consider the vector eq. of the plane passing through the intersection of the planes are $\overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})=7...
Find the intercepts cut off by the plane 2x + y – z = 5.
Solution: It is given that The plane $2 x+y-z=5$ Let us express the equation of the plane in intercept form $x / a+y / b+z / c=1$ Where $a, b, c$ are the intercepts cut-off by the plane at $x, y$...
Find the vector and Cartesian equations of the planes
(a) that passes through the point 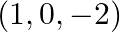 and the normal to the plane is
and the normal to the plane is 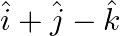
(b) that passes through the point 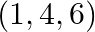 and the normal vector to the plane is
and the normal vector to the plane is 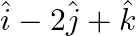
Solution: (a) That passes through the point $(1,0,-2)$ and the normal to the plane is $\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$ Let's say that the position vector of the point $(1,0,-2)$...
Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector 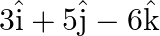
Solution: It is given that, The vector $3 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}-6 \hat{\mathrm{k}}$ Vector equation of the plane with position vector $\overrightarrow{\mathrm{r}}$ is $\vec{r} \cdot...
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = 1
Solution: (a) $z=2$ It is given that The eq. of the plane, $z=2$ or $0 x+0 y+z=2 \ldots (1) .$ The direction ratio of the normal $(0,0,1)$ Using the formula, $\begin{array}{l}...
Find the shortest distance between the lines whose vector equations are 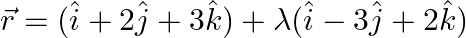 and
and 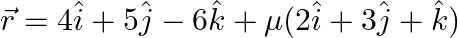
Solution: It is known to us that shortest distance between two lines $\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}$ and $\vec{r}=\overrightarrow{a_{2}}+\mu \overrightarrow{b_{2}}$...
A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR.
Let E1 be the event that the letter comes from TATA NAGAR, E2 be the event that the letter comes from CALCUTTA And, E3 be the event that on the letter, two consecutive letters TA are visible Now,...
Find the equation of the line in vector and in Cartesian form that passes through the point with position vector 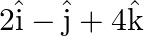 and
and 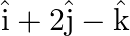 . is in the direction
. is in the direction
Solution: Given: Vector equation of a line that passes through a given point whose position vector is $\vec{a}$ and parallel to a given vector $\vec{b}$ is $\vec{r}=\vec{a}+\lambda \vec{b}$ Let,...
Show that the three lines with direction cosines 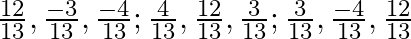 Are mutually perpendicular.
Are mutually perpendicular.
Solution: Consider the direction cosines of $L_{1}, L_{2}$ and $L_{3}$ be $l_{1}, m_{1}, n_{1} ; l_{2}, m_{2}, n_{2}$ and $l_{3}, m_{3}, n_{3}$. It is known that If $\mathrm{f}_{1}, \mathrm{~m}_{1},...
Lifetimes of the molecules in the excited states are often measured by using pulsed radiation source of duration nearly in the nanosecond range. If the radiation source has the duration of 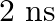 and the number of photons emitted during the pulse source is
and the number of photons emitted during the pulse source is 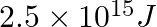 , calculate the energy of the source.
, calculate the energy of the source.
Frequency of radiation $(\nu)$, $\nu=\frac{1}{2.0 \times 10^{-9} s}$ $\nu=5.0 \times 10^{8} s^{-1}$ Energy $(E)$ of source $=$ Nhv Where, $N$ is the no. photons emitted $\mathrm{h}$ is Planck's...
Arrange the following type of radiations in increasing order of frequency: (a) radiation from microwave oven (b) amber light from traffic signal (c) radiation from FM radio (d) cosmic rays from outer space and (e) X-rays.
The following is the frequency order in ascending order: Radiation from FM radio < amber light < radiation from microwave oven < X- rays < cosmic rays The following is the increasing...
Explain, giving reasons, which of the following sets of quantum numbers are not possible.
a) 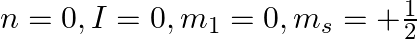
b) 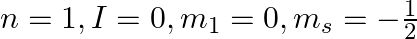
c) 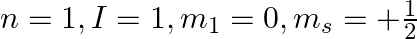
d) 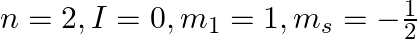
e) 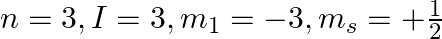
f) 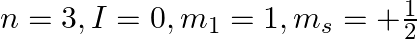
a) This is not possible. The number n cannot be zero. (b) Possible. (c) This is not possible. The value of l can't be the same as the value of n. (d) This is not possible. Because mt can't be 1 when...
What is the lowest value of n that allows g orbitals to exist?
For g-orbitals, l = 4. The possible values of ‘l’ range from 0 to (n-1),. For any given value of ‘n’, Hence, least value of n = 5, l = 4 (g orbital),
(II) What are the atomic numbers of elements whose outermost electrons are represented by (a) 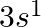 (b)
(b) 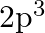 and (c)
and (c) 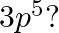
(II) (a) $3 \mathrm{~s}^{1}$ Complete electronic configuration: $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{6} 3 \mathrm{~s}^{1}$ Total no. electrons in the atom $=2+2+6+1=11 \quad...
The electron energy in hydrogen atom is given by 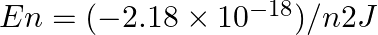 . Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Required energy for the ionization from $\mathrm{n}=2$ is: $ \begin{array}{l} \Delta E=E_{\infty}-E_{2} \\ =\left[\left(\frac{-\left(2.18 \times...
What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is 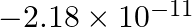 ergs. The ground-state electron energy is
ergs. The ground-state electron energy is 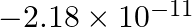 ergs.
ergs.
$ E_{5}=\frac{-\left(2.18 \times 10^{-18}\right) Z^{2}}{(n)^{2}} $ Where, $Z$ denotes the atom's atomic number Ground state energy $=-2.18 \times 10^{-11}$ ergs $=-2.18 \times 10^{-11} \times...
Calculate the wavenumber for the longest wavelength transition in the Balmer series of atomic hydrogen.
The Balmer series of the hydrogen emission spectrum, ni = 2. Hence, wavenumber expression ν is: $ \bar{\nu}=\left[\frac{1}{(2)^{2}}-\frac{1}{n_{f}^{2}}\right]\left(1.097 \times 10^{7}...
How can the production of dihydrogen, obtained from ‘coal gasification’, be increased?
Solution: By the course of coal gasification, dihydrogen is created as $C_{(g)}+H_{2} O_{(g)} \rightarrow C O_{(g)}+H_{2(g)}$ [C-Coal] Response with carbon monoxide with steam within the sight of an...
Write the negation of the following simple statements
(i) All similar triangles are congruent.
(ii) Area of a circle is same as the perimeter of the circle.
(i) "Not p" is the negation of the assertion p. The negation of p is represented by $\sim p$. The truth value of $\sim p$ is the opposite of the truth value of p. The negation of the statement is...
Write the negation of the following simple statements
(i) 2 is not a prime number.
(ii) Every real number is an irrational number.
(i) "Not p" is the negation of the assertion p. The negation of p is represented by $\sim p$. The truth value of $\sim p$ is the opposite of the truth value of p. The negation of the statement is “2...
Write the negation of the following simple statements
(i) The number 17 is prime.
(ii) 2 + 7 = 6.
(i) "Not p" is the negation of the statement p. The negation of p is represented by the "$\sim p$." The truth value of $\sim p$ is the opposite of the truth value of p. The negation of the statement...
Find the component statements of the following compound statements.
(i) √7 is a rational number or an irrational number.
(ii) 0 is less than every positive integer and every negative integer.
(i) A compound statement is made up of two or more statements (Components). As a result, the components of the given statement 7are a rational or irrational number, respectively. p: √7is a rational...
Find the component statements of the following compound statements.
(i) Number 7 is prime and odd.
(ii) Chennai is in India and is the capital of Tamil Nadu.
(i) A compound statement is made up of two or more statements (Components). As a result, the elements of the provided statement "Number 7 is prime and odd" are as follows: p: The number 7 is prime....
Which of the following sentences are statements? Justify
(i) Where is your bag?
(ii) Every square is a rectangle.
(i) If a statement is true or false but not both, it is a declarative sentence. "Where is your bag?" is a question in this context. As a result, it is not a statement. (ii) Every square is a...
Which of the following sentences are statements? Justify
(i) A triangle has three sides.
(ii) 0 is a complex number.
(i) A statement is a declarative sentence if it is either true or false but not both. Hence, it is a true statement (ii) If a statement is true or false but not both, it is a declarative sentence....
The two successive terms in the expansion of 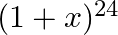 whose coefficients are in the ratio 1: 4 are
whose coefficients are in the ratio 1: 4 are
(A) 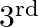 and
and 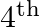
(B) 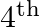 and
and 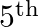
(C) 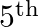 and
and 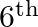
(D) 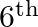 and
and 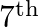
(C) $5^{\text {th }}$ and $6^{\text {th }}$ Explanation: Let $(r+1)^{\text {th }}$ and $(r+$ 2 ) th term be the two successive terms in the expansion of $(1+x)^{24}$. Now, $T_{r+1}={ }^{24} C_{r}...
The total number of terms in the expansion of 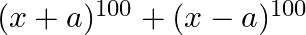 after simplification is
after simplification is
(A) 50
(B) 202
(C) 51
(D) none of these
(C) 51 Explanation: Given expression is $(x+a)^{100}+(x-a)^{100}$ $\begin{aligned} =&\left({ }^{100} C_{0} x^{100}+{ }^{100} C_{1} x^{99} a+{ }^{100} C_{2} x^{98} a^{2}+\ldots\right) \\...
Find 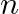 in the binomial
in the binomial ![Rendered by QuickLaTeX.com \left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^{n}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b941f4ec469c3c55a0487ec33d7c20a1_l3.png) , if the ratio of
, if the ratio of 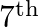 term from the beginning to the
term from the beginning to the 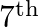 term from the end is
term from the end is 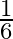 .
.
Given expression is $\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^{n}$ Now, the $7^{\text {th }}$ term from beginning will be, $T_{7}=T_{6+1}={ }^{n}...
If the coefficient of second, third and fourth terms in the expansion of 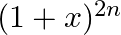 are in A.P. Show that
are in A.P. Show that 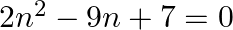 .
.
Given function is $(1+x)^{2 n}$ ${ }^{2 n} C_{1},{ }^{2 n} C_{2}$ and ${ }^{2 n} C_{3}$ are the Coefficient of $2^{\text {nd }}, 3^{\text {rd }}$ and $4^{\text {th }}$ terms are respectively. ${...
Find the sixth term of the expansion 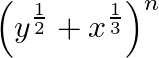 if the binomial coefficient of the third term from the end is
if the binomial coefficient of the third term from the end is 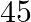
Given function is $\left(y^{1 / 2}+x^{1 / 3}\right)^{n}$ Given the binomial coefficient of the third phrase from the beginning, $=45$ So, ${ }^{n} C_{n-2}=45$ The above expression can be re-written...
Find the coefficient of 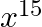 in the expansion of
in the expansion of 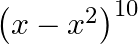
Given function is $\left(x-x^{2}\right)^{10}$ $T_{r+1}={ }^{10} C_{r} x^{10-r}\left(-x^{2}\right)^{r}=(-1)^{r 10} C_{r} x^{10-r} x^{2 r}=(-1)^{r 10} C_{r} x^{10+r}$ For the coefficient of $x^{15}$,...
Find the middle term (terms) in the expansion of
(i) 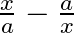
(ii) 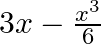
(i) Given function is $\left(\frac{x}{a}-\frac{a}{x}\right)^{10}$ Here, Index of $n$ is $10$ which is even number. So, there is one middle term which is $(10 / 2+1)^{\text {th }}$ term that is...
Find the term independent of  in the expansion of
in the expansion of 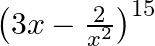
Given function is $\left(3 x-\frac{2}{x^{2}}\right)^{15}$ We know from the standard formula of $T_{r+1}$ we get, $\mathrm{T}_{r+1}={ }^{15} C_{r}(3 x)^{15-r}\left(\frac{-2}{x^{2}}\right)^{r}={...
If the term free from  in the expansion of
in the expansion of 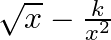 is 405, find the value of k.
is 405, find the value of k.
Given is, $\sqrt{x}-\frac{k}{x^{2}}$ From the standard formula of $T_{r+1}$ we know, $T_{r+1}={ }^{10} C_{r}(\sqrt{x})^{10-r}\left(\frac{-k}{x^{2}}\right)^{r}={ }^{10}...
Find the term independent of  , in the expansion of
, in the expansion of 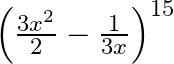
Given function is $\left(\frac{3 x^{2}}{2}-\frac{1}{3 x}\right)^{15}$ We know, the standard formula of $T_{r+1}$ will be, $T_{r+1}={ }^{15} C_{r}\left(\frac{3...
A helicopter of mass 2000 kg rises with a vertical acceleration of 15 m/s2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the a) force on the floor of the helicopter by the crew and passengers b) action of the rotor of the helicopter on the surrounding air c) force on the helicopter due to the surrounding air
Given, M = 2000 kg helicopter mass m = 500 kg m = 500 kg m = 500 kg m = 500 kg m = 500 kg m = 500 kg Helicopter acceleration with crew and passengers = 15 m/s2 a) Force exerted by the crew and...
A racing car travels on a track ABCDEFA. ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The coefficient of friction on the road is μ = 0.1. The maximum speed of the car is 50 m/s. Find the minimum time for completing one round.
Time taken from $A$ to $B$ to $C$ $\mathrm{S} 1=$ length $\mathrm{pf}$ path $=3 / 42 \pi(2 \mathrm{R})=300 \pi \mathrm{m}$ $\mathrm{V} 1=$ speed(maximum) along the circular path of the car $...
Below figures show (vx, t) and (vy, t) diagrams for a body of unit mass. Find the force as a function of time.
For graph a) $ \begin{array}{l} v_{x}=2 t \text { for } 0<t<1 s \\ a_{x}=2 / 1 \text { for } 0<t<1 s \\ v_{x}=2(2-t) \text { for } 1<t<2 s \\ a_{x}=-2 / 1=-2 \text { for }...
When a body slides down from rest along a smooth inclined plane making an angle of 45 degree with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the coefficient of friction between the body and the rough plane.
The inclined plane angle is $45^{\circ}$ such that $ \begin{array}{l} u=0 \\ s=s \\ t=T \\ a=g \sin 45^{\circ}=g / \sqrt{2} \\ s=u t+1 / 2 a t^{2} \\ s=g T^{2} / 2 \sqrt{2} \end{array} $ $...
A bock of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the ginger to hold the block against the wall?
F is the force exerted by the finger on a body of mass M that is resting on the wall. Using the balanced state as a starting point, $ \begin{array}{l} \mathrm{F}=\mathrm{N} \\ \mathrm{f}=\mathrm{Mg}...
Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in the figure. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 m/s2.
The acceleration of the whole system is, $\mathrm{a}=2 \mathrm{~m} / \mathrm{s} 2$ $ \begin{array}{l} \mathrm{m} 1=5 \mathrm{~kg} \\ \mathrm{~m} 2=3 \mathrm{~kg} \\ \mathrm{~g}=9.8 \mathrm{~m} /...
Why does a child feel more pain when falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
When a kid falls on a hard cement floor, the child feels more pain than when the child falls on soft muddy ground in the yard, since the time it takes the child to stop on the cemented ground is...
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
F1 is the force exerted on the heavy box, which is equal to F1 and is resisted by the lesser frictional force f1. F = Fs, which is the maximum static frictional force, is required for the box to...
The velocity of a body of mass 2 kg as a function of t is given by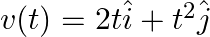 Find the momentum and the force acting on it at time t = 2 sec.
Find the momentum and the force acting on it at time t = 2 sec.
m=2kg $ \underset{v}{\rightarrow}(t)=2 t \hat{i}+t^{2} \hat{j} $ $ \vec{v} \text { at } 2 \mathrm{sec}, \underset{v}{\vec{v}}(2 t)=2(2 t) \hat{i} 2^{2} \hat{j}, v(2)=4 \hat{i}+4 \hat{j} $ $ \text {...
solve the following:
Solution:
Find the equation of a circle which touches both the axes and the line 3x – 4y + 8 = 0 and lies in the third quadrant.
The equation of the given circle is \[{{x}^{2}}~+\text{ }{{y}^{2}}~+\text{ }4x\text{ }+\text{ }4y\text{ }+\text{ }4\text{ }=\text{ }0.\]
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
Given lines are 6x – 8y + 8 = 0 and 6x – 8y – 7 = 0. Distance d between two parallel lines y = mx + c1 and y = mx + c2 is given by d = |C1–C2|/√(A2 + B2 ) These parallel lines are tangent to a...
Consider the non-empty set consisting of children in a family and a relation R defined as aRb if a is brother of b. Then R is (A) symmetric but not transitive (B) transitive but not symmetric (C) neither symmetric nor transitive (D) both symmetric and transitive
The correct option is (B) transitive but not symmetric Given aRb ⇒ a is brother of b. This does not mean b is also a brother of a as b can be a sister of a. Therefore, R is not symmetric. aRb ⇒ a is...
. Let ![Rendered by QuickLaTeX.com \[\mathbf{A}\text{ }=\text{ }\left\{ \mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3},\text{ }\ldots \text{ }\mathbf{9} \right\}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4bba703b875f44961cf66438db00c2aa_l3.png)
and R be the relation in A ×A defined by (a, b) R (c, d) if a + d = b + c for (a, b), (c, d) in ![Rendered by QuickLaTeX.com \[A\text{ }\times A\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b2d867ff818b6c236e399d822f63f0a7_l3.png)
. Prove that R is an equivalence relation and also obtain the equivalent class ![Rendered by QuickLaTeX.com \[\left[ \left( \mathbf{2},\text{ }\mathbf{5} \right) \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3affb3b24e311584fc304dd1f72979fc_l3.png)
.
Given, \[\mathbf{A}\text{ }=\text{ }\left\{ \mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3},\text{ }\ldots \text{ }\mathbf{9} \right\}\]and (a, b) R (c, d) if a + d = b + c for \[\left( a,\text{ }b...
Let R be relation defined on the set of natural number N as follows: ![Rendered by QuickLaTeX.com \[\mathbf{R}\text{ }=\text{ }\{\left( \mathbf{x},\text{ }\mathbf{y} \right):\text{ }\mathbf{x}\in \mathbf{N},\text{ }\mathbf{y}\in \mathbf{N},\text{ }\mathbf{2x}\text{ }+\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{41}\}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-88df5ebd7ad6cdd01200d5d66cf2b418_l3.png)
. Find the domain and range of the relation R. Also verify whether R is reflexive, symmetric and transitive.
Given function: \[\mathbf{R}\text{ }=\text{ }\{\left( \mathbf{x},\text{ }\mathbf{y} \right):\text{ }\mathbf{x}\in \mathbf{N},\text{ }\mathbf{y}\in \mathbf{N},\text{ }\mathbf{2x}\text{ }+\text{...
. If A = ![Rendered by QuickLaTeX.com \[\left\{ \mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3},\text{ }\mathbf{4}\text{ } \right\}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ddb4a1a003ed727977a64339fa0c6859_l3.png)
,define relations on A which have properties of being: (a) reflexive, transitive but not symmetric (b) symmetric but neither reflexive nor transitive (c) reflexive, symmetric and transitive.
According to the question, \[A\text{ }=\text{ }\left\{ 1,\text{ }2,\text{ }3 \right\}\]. (i) Let \[{{R}_{1}}~=\text{ }\left\{ \left( 1,\text{ }1 \right),\text{ }\left( 1,\text{ }2 \right),\text{...
The domain of the function by f(x) = ![Rendered by QuickLaTeX.com \[\mathbf{si}{{\mathbf{n}}^{-\mathbf{1}}}~\sqrt{\left( \mathbf{x}\text{ }\text{ }\mathbf{1} \right)}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dfbf35cc7cb2d872feaf569485ef4904_l3.png)
is (a) ![Rendered by QuickLaTeX.com \[\left[ \mathbf{1},\text{ }\mathbf{2} \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fcfcb28dd59583bc3e7a020a8cf5f451_l3.png)
(b) ![Rendered by QuickLaTeX.com \[\left[ -\mathbf{1},\text{ }\mathbf{1} \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b21f7411312e08e9e9c76b1a5369f211_l3.png)
(c) ![Rendered by QuickLaTeX.com \[\left[ \mathbf{0},\text{ }\mathbf{1} \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4951cedbbb831e919142a21d14151c6a_l3.png)
(d) none of these
The correct option is (a) \[\left[ \mathbf{1},\text{ }\mathbf{2} \right]\] We know that, \[si{{n}^{-1}}~x\] is defined for \[x\in \left[ -1,\text{ }1 \right]\] So, f(x) =...
Find the derivative of 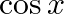 from first principle.
from first principle.
Assume, $f(x) = \cos x$. Then, $f(x + h) = \cos (x + h)$. Using first principle we get, ${{\text{f}}^\prime }({\text{x}}) = \mathop {\lim }\limits_{h \to 0} \frac{{{\text{f}}({\text{x}} +...
Evaluate 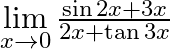 .
.
We are given, $\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x + 3x}}{{2x + \tan 3x}}$. Multiplying and dividing the numerator by $2x$ then, $\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x +...
Evaluate 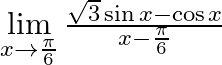 .
.
We are given, $\mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{\sqrt 3 \sin x - \cos x}}{{x - \frac{\pi }{6}}}$ Simplifying the numerator, $\sqrt 3 {\sin ^^\circ } - \cos x = 2\left(...
Evaluate 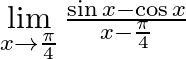 .
.
We are given, $\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin x - \cos x}}{{x - \frac{\pi }{4}}}$ $\sin x - \cos x = \sqrt 2 \left( {\frac{{\sin x}}{{\sqrt 2 }} - \frac{{\cos x}}{{\sqrt 2...
Evaluate 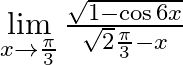 .
.
We are given, $\mathop {\lim }\limits_{x \to \frac{\pi }{3}} \frac{{\sqrt {1 - \cos 6x} }}{{\sqrt 2 \frac{\pi }{3} - x}}$. Using the identity, $\cos 6x = 1 - 2{\sin ^2}3x$ to get, $\mathop {\lim...
Evaluate 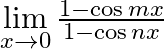 .
.
We are given, $\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos mx}}{{1 - \cos nx}}$ Using the identities, $\cos mx = 1 - 2{\sin ^2}\frac{{mx}}{2}$ and $\operatorname{cosn} x = 1 - 2{\sin...
Evaluate 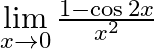 .
.
We are given, $\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 2x}}{{{x^2}}}$. Using the identity, $\cos 2x = 1 - 2{\sin ^2}x$ to get, $\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos...
Evaluate 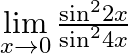 .
.
We are given, $\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}2x}}{{{{\sin }^2}4x}}$ To simplify we have to multiply and divide the numerator and denominator by $\frac{{4{x^2}}}{{16{x^2}}}$ to...
Find 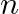 if
if 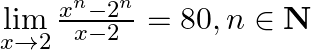 .
.
We are given, $\mathop {\lim }\limits_{x \to 2} \frac{{{x^n} - {2^n}}}{{x - 2}} = 80,n \in {\mathbf{N}}$ Using the formula, $\mathop {\lim }\limits_{x \to a} \frac{{{x^n} - {a^n}}}{{x - a}} = n{a^{n...
Evaluate 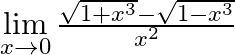 .
.
We are given, $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + {x^3}} - \sqrt {1 - {x^3}} }}{{{x^2}}}$ Rationalize the numerator to get, $ = \mathop {\lim }\limits_{{\text{x}} \to 0}...
Evaluate 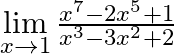 .
.
We solve the given limit by using L. Hospital’s rule which is, If $\mathop {\lim }\limits_{{\text{x}} \to {\text{a}}} \frac{{{\text{f}}({\text{x}})}}{{{\text{g}}({\text{x}})}} = \frac{0}{0}$. Then,...
Evaluate 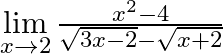 .
.
We are given, $\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{\sqrt {3x - 2} - \sqrt {x + 2} }}$ Rationalize the denominator to get, $ = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} -...
Evaluate 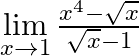 .
.
We are given, $\mathop {\lim }\limits_{x \to 1} \frac{{{x^4} - \sqrt x }}{{\sqrt x - 1}}$ Rationalize the denominator to get, $\mathop {\lim }\limits_{x \to 1} \frac{{{x^4} - \sqrt x }}{{\sqrt x -...
Evaluate 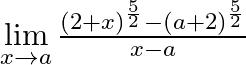 .
.
We are given, $\mathop {\lim }\limits_{x \to a} \frac{{{{(2 + x)}^{\frac{5}{2}}} - {{(a + 2)}^{\frac{5}{2}}}}}{{x - a}}$ $ = \mathop {\lim }\limits_{x \to a} \frac{{{{(2 + x)}^{\frac{5}{2}}} - {{(a...
Evaluate 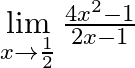 .
.
We are given, $\mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{4{x^2} - 1}}{{2x - 1}}$ $ = \mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{{{(2x)}^2} - 1}}{{2x - 1}}$ Simplifying to get, $ =...
Evaluate: 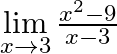 .
.
We are given, $\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{x - 3}}$ $ = \mathop {\lim }\limits_{x \to 3} \frac{{(x - 3)(x + 3)}}{{x - 3}}$ Applying the limits to get, $ = \mathop {\lim...
For the harmonic travelling wave y = 2 cos 2 π(10t-0.0080x+3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of
a) 4 m b) 0.5 m c) λ/2 d) 3 λ/4 e) what is the phase difference between the oscillation of a particle located at x = 100 cm at t = Ts and t = 5s? Answer: According to the questions, we have: y = 2...
In the given progressive waves y = 5 sin (100 πt – 0.4 πx) where y and x are in m, t is in s. What is the
a) amplitude b) wavelength Answer: According to the question, the wave is travelling in +x direction and the equation is given by; y = 5 sin (100 πt – 0.4 πx) The standard equation is as follows: y...
Given below are some functions of x and t to represent the displacement of an elastic wave.
a) y = 5 cos (4x) sin (20t) b) y = 4 sin (5x-t/2) + 3 cos (5x-t/2) c) y = 10 cos [(252-250)πt] cos [(252+250) πt] d) y = 100 cos (100 πt + 0.5x) State which of these represent a) a traveling wave...
If c is r.m.s speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
Answer: We know that the equation for molecules is: $ c=\sqrt{\frac{3RT}{M}} $ Where, M represents the molar mass of the gas $ v=\sqrt{\frac{\gamma P}{\rho }}=\sqrt{\frac{\gamma RT}{M}} $ We know...
The earth has a radius of 6400 km. The inner core of the 1000 km radius is solid. Outside it, there is a region from 1000 km to a radius of 3500 km which is in a molten state. Then again from 3500 km to 6400 km the earth is solid. Only longitudinal (P) waves can travel inside a liquid. Assume that the P wave has a speed of 8 km/s in solid parts and of 5 km/s in liquid parts of the earth. An earthquake occurs at someplace close to the surface of the earth. Calculate the time after which it will be recorded in a seismometer at a diametrically opposite point on the earth if wave travels along diameter?
Answer: According to the question, r1 = 1000 km, r2 = 3500 km, r3 = 6400 km and d1 = 1000 km And we can calculate, d2 = 3500 – 1000 d2 = 2500 km d3 = 6400 – 3500 d3 = 2900 km Expression for the...
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops, and 4 loops, the frequencies are in the ratio 1:2:3:4.
Answer: When n = 1, f1 = v/2L This is known as the fundamental frequency. When n = 2, f2 = 2(v/2L) This is known as the first overtone. When n = 3, f3 = 3(v/2L) This is known as the second overtone....
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water. The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, the maximum intensity of sound is heard. If the room temperature is 20oC, calculate
c) if the water in the tube is replaced with mercury, will there be any difference in your observations? Answer: (c) Sound is reflected into the air column by water and mercury in the tube, forming...
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water. The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, the maximum intensity of sound is heard. If the room temperature is 20oC, calculate
a) speed of sound in air at room temperature b) speed of sound in air at 0oC Answer: According to the question, the frequency of the tuning fork is f = 512 Hz a) When the first maxima are taken...
The pattern of standing waves formed on a stretched string at two instants of time are shown in the figure. The velocity of two waves superimposing to form stationary waves is 360 m/s and their frequencies are 256 Hz.
a) calculate the time at which the second curve is plotted b) mark nodes and antinodes on the curve c) calculate the distance between A’ and C’ Answer: According to the quetion, the frequency of the...
The wave pattern on a stretched string is shown in the figure. Interpret what kind of wave this is and find its wavelength.
Answer: A stationary wave which is at its mean position when the particles at t = T/4 and 3T/4 are at rest. The displacement of medium particles at distances of 10, 20, 30, 40, and 50 cm is always...
A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz still air. The train beings to move with a speed of 10 m/s towards the platform. What is the frequency of the sound for an observer standing on the platform?
Answer: It is given that v0 = 400 Hz and vz = 10 m/s We know that the velocity of sound in air is va = 330 m/s The frequency heard by the observer on the platform is v'. Therefore, we can write: v’...
