Answer : Given: three jobs, I, II and III to be assigned to three persons A, B and C. To find: In how many ways this can be done. Condition: one person is assigned only one job and all are capable...
Answer : To find: number of natural numbers less than 1000 that can be formed from the digits 0, 1, 2, 3, 4, 5 when a digit may be repeated any number of times For forming a 3 digit number less than...
Answer : To find: number of numbers that can be formed from the digits 1, 3, 5, 9 if repetition of digits is not allowed Forming a 4 digit number:4! Forming a 3 digit number:4C3 × 3! Forming a 2...
Answer : To find: Number of 4 digit numbers when a digit may be repeated any number of times The first place has possibilities of any of 9 digits. (0 not included because 0 in starting would make...
Answer : Each letter has 4 possible letter boxes option. So the number of ways in which 5 letters can be posted in 4 letter boxes =4 × 4 × 4 × 4 × 4=45 (Each 4 for each letter.)
Answer : Given:6 rings and 4 fingers. Each ring has 4 different fingers that they can be worn. So total number of ways in which 6 rings of different types can be worn in 4 fingers =4 × 4 × 4 × 4 × 4...
Answer : Given: A gentleman has 6 friends to invite. He has 3 servants to carry the cards. Each friend can be invited by 3 possible number of servants. So the number of ways of inviting 6 friends...
Answer : Given: 5 objective-type question, each question having 4 choices. To find: the number of ways of answering them. Each objective-type question has 4 choices. So the total number of ways of...
Answer : Given: 20 students. The number of ways of giving first and second prizes in mathematics to a class of 20 students=20 × 19. (First prize can be given to any one of the 20 students but the...
Answer : Given: a set of five true – false questions. To find: the maximum number of students in the class. Condition: no student has written the all correct answer and no two students have given...
Answer : A bulb can be good or defective, so there are 2 different possibilities of a bulb. So number of all possible outcomes (of all bulbs)=2 × 2 × 2=8
Answer : Given: 36 teachers are there in a school. To find: Number of ways in which one principal and one vice-principal can be appointed. There are 36 options of appointing principal and 35 option...
Answer : To find: types of February calendars that can be prepared. There are two factors to develop FEBRUARY metallic calendars The day on the start of the year of which possibility=7 Whether the...
Answer : Given: Two sets: {1, 2, 3} & {2, 3, 4} To find: number of A.P. with 10n terms whose first term is in the set {1, 2, 3} and whose common difference is in the set {2, 3, 4} Number of...
Answer : This is the example of Cartesian product of two sets. The pairs in which the first entry is an element of A and the second is an element of B are : (2,0),(2,1),(3,0),(3,1),(5,0),(5,1) ⇒ 3 ×...
Answer : Given: first 10 letters of the English alphabet. In 4 letter code for first position there are 10 possibilities for second position there are 9 possibilities, for third position there are 8...
Answer : (a) A coin is tossed three times So possible number of outcomes=23=8 (HHH,HHT,HTH,HTT,THH,THT,TTH,TTT) (b) i) A coin is tossed four times So possible number of outcomes=24=16...
Answer : To find: number of ways in which 5 ladies draw water from 5 taps. Condition: no tap remains unused The condition given is that no well should remain unused. So possible number of ways are:...
Answer : Given: 12 steamers plying between A and B. To find: number of ways the round trip from A can be made. The steamer which will go from A to B will be returning back, since the given condition...
Answer : Given: 5 routes from A to B and 3 routes from B to C. To find: number of different routes from A to C via B. Let E1 be the event : 5 routes from A to B Let E2 be the event : 3 routes from B...
: 
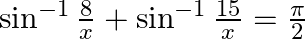
Solution: To find: value of $x$ Given: $\sin ^{-1} \frac{\mathrm{g}}{\mathrm{x}}+\sin ^{-1} \frac{15}{\mathrm{x}}=\frac{\pi}{2}$ We know $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$...
Answer : Given: 10 buses running between Delhi and Agra. To Find: Number of ways a man can go from Delhi to Agra and return by a different bus. There are 10 buses running between Delhi and Agra so...
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{17}}+\cos ^{-1} \frac{9}{\sqrt{85}}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
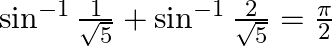
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{5}}+\sin ^{-1} \frac{2}{\sqrt{5}}=\frac{\pi}{2}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
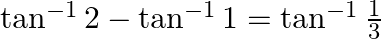
Solution: To Prove: $\tan ^{-1} 2-\tan ^{-1} 1=\tan ^{-1} \frac{1}{3}$ Formula Used: $\tan ^{-1} \mathrm{x}-\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}-\mathrm{y}}{1+\mathrm{xy}}\right)$...
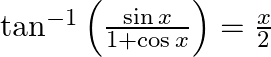
Solution: To Prove: $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)=\frac{x}{2}$ Formula Used: 1) $\sin A=2 \times \sin \frac{A}{2} \times \cos \frac{A}{2}$ 2) $1+\cos A=2 \cos ^{2} \frac{A}{2}$...
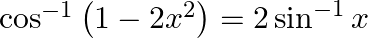
Solution: To Prove: $\cos ^{-1}\left(1-2 x^{2}\right)=2 \sin ^{-1} x$ Formula Used: $\cos 2 A=1-2 \sin ^{2} A$ Proof: $\operatorname{LHS}=\cos ^{-1}\left(1-2 x^{2}\right) \ldots(1)$ Let $x=\sin A...
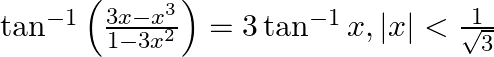
Solution: To Prove: $\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)=3 \tan ^{-1} x$ Formula Used: $\tan 3 A=\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}$ Proof: $\text { LHS }=\tan...
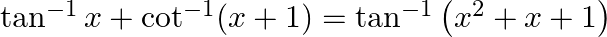
Solution: To Prove: $\tan ^{-1} x+\cot ^{-1}(x+1)=\tan ^{-1}\left(x^{2}+x+1\right)$ Formula Used: 1) $\cot ^{-1} \mathrm{x}=\tan ^{-1} \frac{1}{\mathrm{x}}$ 2) $\tan ^{-1} \mathrm{x}+\tan ^{-1}...
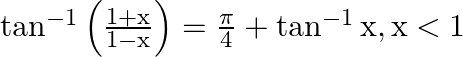
Solution: To Prove: $\tan ^{-1}\left(\frac{1+x}{1-x}\right)=\frac{\pi}{4}+\tan ^{-1} x$ Formula Used: $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ Proof: $\mathrm{LHS}=\tan...
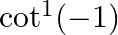
Solution: $\cot ^{-1}(-1)=\pi-\cot ^{-1}(1)$ [Formula: $\left.\cot ^{-1}(-x)=\pi-\cot ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{4} \\ =\frac{3 \pi}{4} \end{array}$
Answer : This equation is a quadratic equation. Solution of a general quadratic equation ax2 + bx + c = 0 is given by: Given: ⇒x2 + 2 = 0 ⇒x2 = -2 ⇒x = ± √ (-2) But we know that √ (-1) = i ⇒ x = ±√2...
Answer:
Answer:
Answer:
Answer:
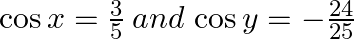, where 
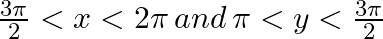, find the values of (iii) tan (x + y)Answer: (iii)Here first we will calculate value of tanx and tany,
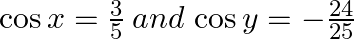, where 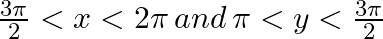, find the values of (i) sin (x + y) (ii) cos (x – y)Answer: Given: $\cos x=\frac{3}{5}\,and\,\cos y=-\frac{24}{25}$ We will first find out value of sinx and siny, (i)sin(x + y) = sinx.cosy + cosx.siny (ii)cos(x - y) = cosx.cosy +...
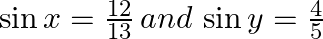, where 
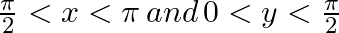, find the values of (iii) tan (x – y)Answer: Given: $\sin x=\frac{12}{13}\,and\,\sin y=\frac{4}{5}$ (iii)Here first we will calculate value of tanx and tany
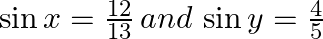, where 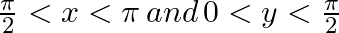, find the values of (i) sin (x + y) (ii) cos (x + y)Answer: Given: $\sin x=\frac{12}{13}\,and\,\sin y=\frac{4}{5}$ Here we will find values of cosx and cosy (i) sin(x + y) = sinx.cosy + cosx.siny (ii)cos(x + y) = cosx.cosy +...
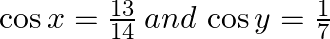, prove that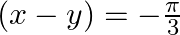 
Answer: Given: $\cos x=\frac{13}{14}\,and\,\cos y=\frac{1}{7}$ Now we will calculate value of sinx and siny Hence, Cos(x - y) = cosx.cosy + sinx.siny
Answer : Given: ⇒ x + 3i = (1 – i)(2 + iy) ⇒ x + 3i = 1(2 + iy) – i(2 + iy) ⇒ x + 3i = 2 + iy – 2i – i2y ⇒ x + 3i = 2 + i(y – 2) – (-1)y [i2 = -1] ⇒ x + 3i = 2 + i(y – 2) + y ⇒ x + 3i = (2 + y) +...