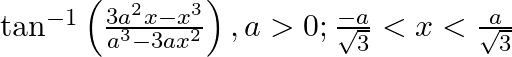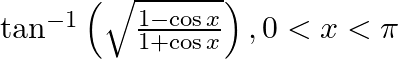Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
Find the principal value of each of the following :
(i) 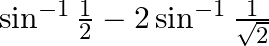
(ii) 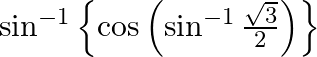
Solution: (i) We can write the given question as, $\sin ^{-1} \frac{1}{2}-2 \sin ^{-1} \frac{1}{\sqrt{2}}=\sin ^{-1} \frac{1}{2}-\sin ^{-1}\left(2 \times \frac{1}{\sqrt{2}}...
Find the principal value of the following:
(i) 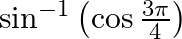
(ii) 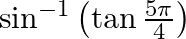
Solution: (i) Suppose $\sin ^{-1}\left(\cos \frac{3 \pi}{4}\right)=\mathrm{y}$ Therefore we can write the above equation as $\sin \mathrm{y}=\cos \frac{3 \pi}{4}=-\sin \left(\pi-\frac{3...
Find the principal value of the following:
(i) 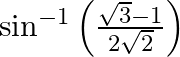
(ii) 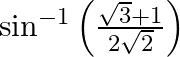
Solution: (i) It is given that functions can be written as $\sin ^{-1}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\sin ^{-1}\left(\frac{\sqrt{3}}{2 \sqrt{2}}-\frac{1}{2 \sqrt{2}}\right) $Taking $1 /...
Find the principal value of the following:
(i) 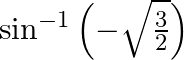
(i i) 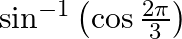
Solution: $(i)$ Let $\sin ^{-1}\left(\frac{-\sqrt{3}}{2}\right)=y$ Therefore $\sin y=\left(\frac{-\sqrt{3}}{2}\right)$ $\begin{array}{l} =-\sin \left(\frac{\pi}{3}\right) \\ =\sin...
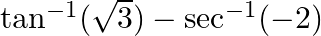 is equal to (A) \pi (B)
is equal to (A) \pi (B) 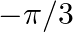 (C)
(C) 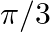 (D)
(D) 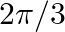
The correct option is Option (B). $\tan ^{-1}(\sqrt{3})-\sec ^{-1}(-2)=\tan ^{-1}(\tan \pi / 3)-\sec ^{-1}(-\sec \pi / 3)$ $=\pi / 3-\sec ^{-1}(\sec (\pi-\pi / 3))$ $=\pi / 3-2 \pi / 3=-\pi /...
If 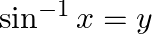 , then (A)
, then (A) 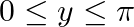 (B)
(B) 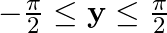 (C)
(C) 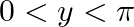 (D)
(D) 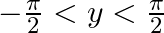
The correct option is Option (B) . Since, $\sin ^{-1} x=y$, The range of $\sin ^{-1}$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ Therefore, $-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$
Find the values of the following: 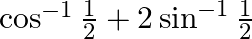
Assume $\cos ^{-1}\left(\frac{1}{2}\right)=x$. Then, $\cos x=\frac{1}{2}=\cos \left(\frac{\pi}{3}\right)$ $\cos ^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{3}$ Assume, $\sin...
Find the principal values of the following: 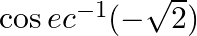
${\cos e c^{-1}(-\sqrt{2})}$ assume, $y=\operatorname{cosec}^{-1}(-\sqrt{2})$ $\operatorname{cosec} y=-\sqrt{2}$ $\cos e c y=\cos e c \frac{-\pi}{4}$ Since$\operatorname{cosec}^{-1}$ is...
Find the principal values of the following: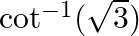
${\cot ^{-1}(\sqrt{3})}$ $y=\cot ^{-1}(\sqrt{3})$ $\cot y=\sqrt{3}$ $\cot y=\pi / 6$ Since $\cot ^{1}$ is $[0, \pi]$ Therefore, ${\cot ^{-1}(\sqrt{3})}$ is $\pi / 6$.
Find the principal values of the following:\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)$
\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)$ $y=\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)$ $\sec y=2 / \sqrt{3}$ $\sec y=\sec \frac{\pi}{6}$ Since $\sec ^{-1}$ is $[0, \pi]$ Therefore, $\sec...
Find the principal values of the following: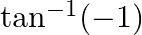
$\tan ^{-1}(-1)$ Let $y=\tan ^{-1}(-1)$ $\tan (y)=-1$ $\tan y=-\tan \pi / 4$ $\tan y=\tan \left(-\frac{\pi}{4}\right)$ Since tan $^{-1}$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ Therefore,...
Find the principal values of the following: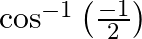
$y=\cos ^{-1}\left(\frac{-1}{2}\right)$ $\cos y=-1 / 2$ Since principle is $\cos ^{-1}$ is [0, \pi] Therefore, $\cos ^{-1}\left(\frac{-1}{2}\right)$ is $2 \pi / 3$.
Find the principal values of the following: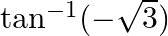
$\tan ^{-1}(-\sqrt{3})$ Let $y=\tan ^{-1}(-\sqrt{3})$ $\tan y=-\tan \pi / 3$ or $\tan y=\tan (-\pi / 3)$ Since range is tan $^{-1}$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ Therefore,$\tan...
Find the principal values of the following: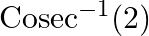
Let $y=\operatorname{cosec}^{-1}(2)$ $\operatorname{Cosec} y=2$ since,$\operatorname{cosec} \pi / 6=2$ So $\operatorname{cosec} y=\operatorname{cosec} \pi / 6$ Since range is...
Find the principal values of the following: 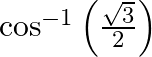
assuming, $y=\cos ^{-1}\left(\frac{\sqrt{3}}{2}\right)$ $\cos y=\cos \pi / 6 \quad(\operatorname{as} \cos \pi / 6=\sqrt{3} / 2)$ $y=\pi / 6$ Since range is $\cos ^{-1}$ is $[0, \pi]$ Therefore,...
Find the principal values of the following: 1. 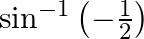
Considering $y=\sin ^{-1}\left(-\frac{1}{2}\right)$ Solveing the above equation, we get $\sin \mathrm{y}=-1 / 2$ since, $\sin \pi / 6=1 / 2$ therefore, $\sin y=-\sin$ $\sin y=\sin...
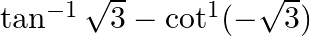 is equal to
is equal to
(A) 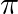
(B) –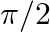
(C) 0
(D) 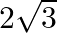
the correct Option is OPTION (B). Reason: $\tan ^{-1} \sqrt{3}-\cot ^{1}(-\sqrt{3})$ can be written as $=\tan ^{-1} \tan \frac{\pi}{3}-\cot ^{-1}\left(-\cot \frac{\pi}{6}\right)$...
![Rendered by QuickLaTeX.com \sin \left[\frac{\pi}{3}-\sin ^{-1}\left(-\frac{1}{2}\right)\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-89ba927cd58dd9b1d74bd9821a287fc2_l3.png) is equal to
is equal to
(A) ${ }^{1 / 2}$ (B) $1 / 3$ (C) ${ }^{1 / 4}$ (D) 1 The corect option is OPTION(D) Reason: solving for: $\sin ^{-1}\left(-\frac{1}{2}\right)$ we get $=\sin (\pi / 2)$ which is equal to...
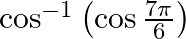 is equal to
is equal to
(A) $7 \mathrm{\pi} / 6$ (B) $5 \mathrm{~m} / 6$ (C) $\pi / 3$ (D) $\pi / 6$ The correct option is Option (B)because, $\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2...
Find the values of each of the expressions in: 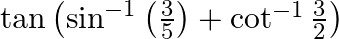
$\tan \left(\sin ^{-1}\left(\frac{3}{5}\right)+\cot ^{-1} \frac{3}{2}\right)$ replacing $\sin ^{-1}\left(\frac{3}{5}\right)by x$ and $\cot ^{-1}\left(\frac{3}{2}\right)by y$ Or $\sin (x)=3 / 5$ and...
Find the values of each of the expressions in: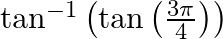
$\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$splitting $\frac{3 \pi}{4}$ as $\frac{(4 \pi-\pi)}{4}$ or $\pi-\frac{\pi}{4}$ and substituting the same given equation we get, $\tan...
Find the values of each of the expressions in :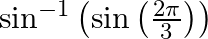
$\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ splitting $\frac{2 \pi}{3}$ as $\frac{(3 \pi-\pi)}{3}$ or $\pi-\frac{\pi}{3}$ and substitute the same in given equation we get,$\sin...
If 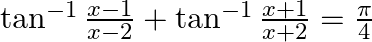 , then find the value of x.
, then find the value of x.
usig the identity:: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1} \frac{x+y}{1-x y}$we conclude: $\tan ^{-1}...
If 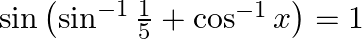 , then find the value of
, then find the value of  .
.
since, $\sin 90$ $=\sin \pi / 2=1$ using the above we get,, $\sin ^{-1} \frac{1}{5}+\cos ^{-1} x=\frac{\pi}{2}$ $\cos ^{-1} x=\frac{\pi}{2}-\sin ^{-1} \frac{1}{5}$ Using identity: $\sin ^{-1} t+\cos...
![Rendered by QuickLaTeX.com \tan \frac{1}{2}\left[\sin ^{-1} \frac{2 x}{1+x^{2}}+\cos ^{-1} \frac{1-y^{2}}{1+y^{2}}\right],|x|<1, y>0](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a3d0089ff967a11fe8c59df47e80a07a_l3.png) and
and 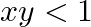
replacing x by $\tan \theta$ and y by $\tan \Phi$, we get, $\tan \frac{1}{2}\left[\sin ^{-1} \frac{2 \tan \theta}{1+\tan ^{2} \theta}+\cos ^{-1} \frac{1-\tan ^{2} \phi}{1+\tan ^{2} \phi}\right]$...
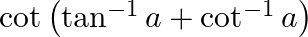 }
}
$\cot \left(\tan ^{-1} a+\cot ^{-1} a\right)=\cot \pi / 2=0$ formula used is: $\tan ^{-1} a+\cot ^{-1} a=\pi / 2$
Find the values of each of the following:![Rendered by QuickLaTeX.com \tan ^{-1}\left[2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-388f85be8482c753cd47645d15dc5ac1_l3.png)
$=\tan ^{-1}\left[2 \cos \left(2 \sin ^{-1} \sin \frac{\pi}{6}\right)\right]$ 8$=\tan ^{-1}\left[2 \cos \left(2 \times \frac{\pi}{6}\right)\right]$ $=\tan ^{-1}(2 \cos \pi / 3)$$=\tan ^{-1}(2 \times...
dividing both numerator and denominator by a $^{\wedge} 3$ we get,$\tan ^{-1}\left(\frac{3\left(\frac{x}{a}\right)-\left(\frac{x}{a}\right)^{3}}{1-3\left(\frac{x}{a}\right)^{2}}\right)$ Putting $x /...
replacing x by $a \sin \theta$, which is equal to $\sin \theta=x / a$ and $\theta=\sin ^{-1}(x / a)$ Substituting the values in the given function, we get $\tan ^{-1}...
tan^-1(cos x-sin x/ cosx + sinx); -pi/4
dividing both numerator and denominator by $\cos x$,we get $\tan ^{-1}\left(\frac{\frac{\operatorname{cox}(x)}{\cos (x)}-\frac{\sin (x)}{\cos (x)}}{\frac{\cos (x)}{\cos (x)}+\frac{\sin (x)}{\cos...
Solution: $\tan ^{-1}\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)=\tan ^{-1}\left(\sqrt{\frac{2 \sin ^{2} \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}}\right)$ $=\tan ^{-1}\left(\frac{\sin...
putting, $x=\sec \theta$, which means $\theta=\sec ^{-1} x$ $\tan ^{-1} \frac{1}{\sqrt{x^{2}-1}}=\tan ^{-1} \frac{1}{\sqrt{\sec ^{2} \theta-1}}$ $=\tan ^{-1} \frac{1}{\sqrt{\tan ^{2} \theta}}$...
putting $x=\tan \theta$ which means $\theta=\tan ^{-1} x$ $\tan ^{-1} \frac{\sqrt{1+x^{2}}-1}{x}=\tan ^{-1}\left(\frac{\sqrt{1+\tan ^{2} \theta}-1}{\tan \theta}\right)$ $=\tan ^{-1}\left(\frac{\sec...
2tan-1 (1/2)+tan-1(1/7)= tan-1(31/17)
identity used is: $2 \tan ^{-1} x=\tan ^{-1} \frac{2 x}{1-x^{2}}$ LHS $=2 \tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{7}$ $=\tan ^{-1} \frac{2 \times \frac{1}{2}}{1-\left(\frac{1}{2}\right)^{2}}+\tan...
$3 \cos ^{-1} x=\cos ^{-1}\left(4 x^{3}-3 x\right), x \in\left[\frac{1}{2}, 1\right]$ identity used is: $\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$ $\operatorname{Putting} x=\cos \theta$...
$3 \sin ^{-1} x=\sin ^{-1}\left(3 x-4 x^{3}\right), x \in\left[-\frac{1}{2}, \frac{1}{2}\right]$ (identity used is: $\sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta$ ) putting $x=\sin \theta$ then...
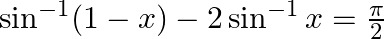 then
then  is equal to
is equal to 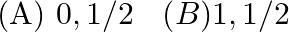 (C) 0 (D)
(C) 0 (D) 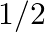
The correct option is OPTION(C): Reason:replacing $\sin ^{-1} x=\theta \quad$ So, $x=\sin \theta$ $\sin ^{-1}(1-x)-2 \sin ^{-1} x=\frac{\pi}{2}$ $\sin ^{-1}(1-x)-2 \theta=\frac{\pi}{2}$ $\sin...
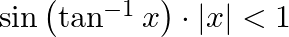 is equal to
is equal to
(A) $\frac{x}{\sqrt{1-x^{2}}}$ (B) $\frac{1}{\sqrt{1-x^{2}}}$ (c) $\frac{1}{\sqrt{1+x^{2}}}$ (D) $\frac{x}{\sqrt{1+x^{2}}}$ The correct Option is OPTION(D) Reason: put $\theta=\tan ^{-1} x$ so that,...
Solve tan-1(1-x/1+x)=1/2 tan-1x, (x>0)
replacingx by $\tan \theta$ $\tan ^{-1}\left(\frac{1-x}{1+x}\right)=\frac{1}{2} \tan ^{-1} x$ $\tan ^{-1}\left(\frac{1-x}{1+x}\right)=\frac{1}{2} \tan ^{-1} x$ $\tan ^{-1}\left(\frac{1-\tan...
Solve: 2tan-1(cos x) = tan-1(2 cosec x)
$2 \tan ^{-1}(\cos x)=\tan ^{-1}(2 \operatorname{cosec} x)$ $\tan ^{-1}\left(\frac{2 \cos x}{1-\cos ^{2} x}\right)=\tan ^{-1}\left(\frac{2}{\sin x}\right)$ $\frac{2 \cos x}{1-\cos ^{2}...
Prove that ????????/????-????/????????????????−????(????/3)= ????/ ???? ????????????−????(????√????/3)
LHS $=\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1} \frac{1}{3}$ $=\frac{9}{4}\left(\frac{\pi}{2}-\sin ^{-1} \frac{1}{3}\right)$ $=\frac{9}{4} \cos ^{-1} \frac{1}{3}$ $\ldots \ldots .(1)$ (identity used...
Prove that ????????????−????(√????+???? −√????−????)/(√????+???? + √????−????) =????/????-????/????????????????−???? ???? , −????√????≤ ???? ≤ ????[Hint: Put x = cos 2 θ]
Putting $x=\cos 2 \theta \quad$ so that, $\theta=\frac{1}{2} \cos ^{-1} x$ LHS $=\tan ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right)$ $=\tan ^{-1}\left(\frac{\sqrt{1+\cos 2...
Prove that cot-1(√????+???????????????? + √????−????????????????)/(√????+???????????????? − √????−????????????????) =????/????, x ∈ (0, π/4)
$1+\sin x$ = $$1+\sin x=\cos ^{2} \frac{x}{2}+\sin ^{2} \frac{x}{2}+2 \cos \frac{x}{2} \sin \frac{x}{2}=\left(\cos \frac{x}{2}+\sin \frac{x}{2}\right)^{2}$$also, $$1-\sin x=\cos ^{2}...
Prove that ????????????−????√????=????/????????????????−????(????−????)/(????+????), x ∈ (0, 1)
Let tan−1 √???? = θ , then, at that point √???? = tan θ Figuring out both the sides tan2 θ = x Presently, substitute the worth of x in 1/2 cos−1 (1−????)/(1+x) , we get = ½ cos-1 (cos 2 θ) = ½ (2 θ)...
Prove that 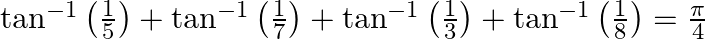
$\mathrm{LHS}=\left(\tan ^{-1}\left(\frac{1}{5}\right)+\tan ^{-1}\left(\frac{1}{7}\right)\right)+\left(\tan ^{-1}\left(\frac{1}{3}\right)+\tan ^{-1}\left(\frac{1}{8}\right)\right)$ Solving the given...
Prove that tan-1(63/16)=sin-1(5/13)+cos-1(3/5)
Settle the articulation, Using character: = 63/16 (θ + ϕ) = tan-1 (63/16) Returning the worth of θ and ϕ, we get tan−1 63) = sin−1 ( 5 ) + cos−1 3) 63/16 Thus Proved.
Prove that ????????????−???? (12/13) + sin-1(3/5) = sin-1(56/65)
Address the articulation, Using personality: sin (θ + ϕ) = sin θ cos ϕ + cos θ sin ϕ = 12/13 x 3/5 + 12/13 x 3/5 = (20+36)/65 = 56/65 or then again sin (θ + ϕ) = 56/65 or then again θ + ϕ) = sin - 1...
Prove that ????????????−???? (4/5 ) + ????????????−???? (12/13) + ????????????−???? (33/65)
Tackle the articulation, Using character: cos (θ + ϕ) = cosθ cos ϕ - sinθ sin ϕ = 4/5 x 12/13 – 3/5 x 5/13 = (48-15)/65 = 33/65 This infers cos (θ + ϕ) = 33/65 or on the other hand θ + ϕ = cos-1...
Prove that ????????????−????/???? + ????????????−????/???? = ????????????−????/????????
Let sin−1 ( 8 ) = ???? then, at that point sin x = 8/17 Once more, cos x = √1 − sin2 ???? = √1 − 64 289= 15/17 Furthermore, tan x = sin x/cos x = 8/15 Once more, Let sin−1/3( ) = ????5 then, at that...
Prove that ???? ????????????−????/ ???? = ????????????−???? /????????
Stage 1: Find the worth of cos x and tan x Allow us to consider sin−1 3 = ????, then, at that point sin x = 3/5 Thus, cos x = √1 − sin2 ???? = √1 − ( ) = 4/5 tan x = sin x/cos x = ¾ Accordingly, x =...
Find the value of the following:
2. ????????????−????(???????????? ????????) First settle for, tan 7???? = tan(???? + ????) = tan ???? Presently: ????????????−1(tan 7????) = tan−1(tan ????) = ???? ∈ (- π/2, π/2) [As tan-1 tan(x) =...
Find the value of the following:
1. ????????????−????(???????????? ????????????/6) First address for, cos 13???? = 6 \[cos\left( 2+ \right)\text{ }6\] \[=\text{ }cos/6\] Presently: cos−1(cos 13????/6) = cos−1(cos ????/6) = ???? ∈...