Answer: Consider, e be the identity element in I+ with respect to * such that a * e = a = e * a, ∀ a ∈ Q – {-1} a * e = a and e * a = a, ∀ a ∈ Q – {-1} a + e + ae = a and e + a + ea = a, ∀ a ∈ Q –...
Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
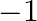with respect to * defined by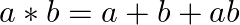 
Assume ‘e’ be the identity element in ${{I}^{+}}$ with respect to * such that $a*e=a=e*a,\forall a\in Q-\left\{ -1 \right\}$ $a*e=a$and $e*a=a,\forall a\in Q-\left\{ -1 \right\}$ $a+e+ae=a$and...
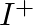of all positive integers defined by 
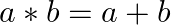for all 
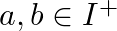.Assume ‘e’ be the identity element in ${{I}^{+}}$ with respect to * such that $a*e=a=e*a,\forall a\in {{I}^{+}}$ $a*e=a$and $e*a,\forall a\in {{I}^{+}}$ $a+e=a$ and $e+a=a$, $\forall a\in {{I}^{+}}$...