Solution: Given that $f(x)$ is differentiable at each $x \in R$ For $x \leq 1$ $f(x)=x^{2}+3 x+a$ i.e. a polynomial for $x>1$ $f(x)=b x+2$, which is also a polynomial As, a polynomial function is...
Find the values of
If 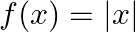 show that
show that 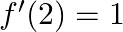
Solution: The given function is $f(x)=|x|$ $\text{Left Hand Derivative}$ at $\mathrm{x}=2$ $\begin{array}{l} \operatorname{Lim}_{x \rightarrow 2^{-}} \frac{f(x)-f(2)}{x-2}=\lim _{h \rightarrow 0}...
Let 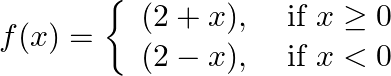 Show that
Show that 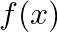 is not derivable at
is not derivable at 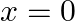 .
.
Solution: The given function $f(x)=\left\{\begin{array}{l}(2+x), \text { if } x \geq 0 ; \\ (2-x), i f x<0\end{array}\right.$ Left Hand Derivative at $x=0$ : $\begin{array}{l}...
Show that function 
Solution: The given function $f(x)=\left\{\begin{array}{l}(1-x), \text { when } x<1 \\ \left(x^{2}-1\right), \text { when } x \geq 1\end{array}\right.$ L.H.L. at $\mathrm{x}=1$ :...
Show that ![Rendered by QuickLaTeX.com f(x)=[x]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8f47443f1f11afcdf4c5b6911afea463_l3.png) is neither continuous nor derivable at
is neither continuous nor derivable at 
Solution: L.H.L. at $x=2$ $\lim _{x \rightarrow 2^{-}} f(x)=\lim _{h \rightarrow 0} f(2-h)=\lim _{h \rightarrow 0}[2-h]=\lim _{h \rightarrow 0} 1=1$ R.H.L. at $x=2$ $\lim _{x \rightarrow 2^{+}}...
Let 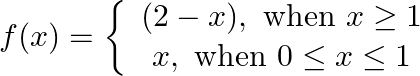 Show that
Show that 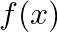 is continuous but not differentiable at
is continuous but not differentiable at 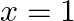
Solution: L.H.L. at $x=1$ $\operatorname{Lim}_{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1} x=1$ $f(x)=x$ is polynomial function and a polynomial function is continuous everywhere R.H.L. at...
Show that 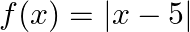 is continuous but not differentiable at
is continuous but not differentiable at 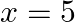
Solution: L.H.L. at $x=5$ $\lim _{x \rightarrow 5^{-}}|x-5|=\lim _{x \rightarrow 5}(5-x)=0$ R.H.L. at $\mathrm{x}=5$ $\lim _{x \rightarrow 5^{+}}|x-5|=\lim _{x \rightarrow 5}(x-5)=0$ Also...
Show that constant function is always differentiable.
Solution: Asumme that $a$ is any constant number. Therefore, $f(x)=a$ $\mathrm{f}^{\prime}(\mathrm{x})=\lim _{\mathrm{h} \rightarrow 0}...
Show that 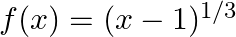 is not differentiable at
is not differentiable at 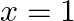
Solution: The given function $f(x)=(x-1)^{1 / 3}$ $\mathrm{Left Hand Derivative}$ at $\mathrm{x}=1$ $\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}} \frac{f(x)-f(1)}{x-1}=\lim _{h...
Show that 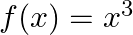 is continuous as well as differentiable at
is continuous as well as differentiable at 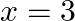
Solution: It is given that: $f(x)=x^{3}$ If a function is differentiable at a point, it is necessary that it is continuous at that point. Left hand derivative at $x=3$ $\begin{array}{l} \lim _{x...
Discuss the continuity of the function 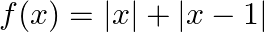 in the interval of
in the interval of ![Rendered by QuickLaTeX.com [-1,2]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-52c22156b1ec8e0e25e594fd399bce34_l3.png)
Solution: The given function $f(x)=|x|+|x-1|$ A function $f(x)$ is said to be continuous on a closed interval $[a, b]$ if and only if, (i) $\mathrm{f}$ is continuous on the open interval...
Locate the point of discontinuity of the function 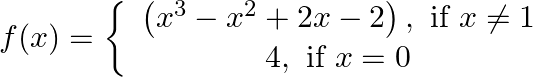
Solution: The given function $f(x)=\left\{\begin{array}{c}\left(x^{3}-x^{2}+2 x-2\right), \text { if } x \neq 1 \\ 4, \text { if } x=1\end{array}\right.$ L.H.L. at $\mathrm{x}=1: \lim _{\mathrm{x}...
Show that 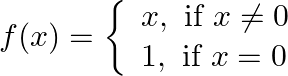 is continuous at each point except 0 .
is continuous at each point except 0 .
Solution: The given function is $f(x)=\left\{\begin{array}{l}x, \text { if } x \neq 0 \\ 1, \text { if } x=0\end{array}\right.$ L.H.L. at $\mathrm{x}=0$ $\lim _{x \rightarrow 0^{-}} f(x)=\lim _{h...
Show that 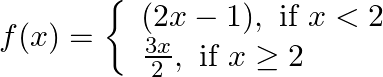 is continuous.
is continuous.
Solution: The given function $f(x)=\left\{\begin{array}{c}(2 x-1), \text { if } x<2 \\ \frac{3 x}{2}, \text { if } x \geq 2\end{array}\right.$ L.H.L. at $x=2$ $\lim _{x \rightarrow 2^{-}}...
Discuss the continuity of ![Rendered by QuickLaTeX.com f(x)=[x]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8f47443f1f11afcdf4c5b6911afea463_l3.png)
Solution: Assume that $n$ be any integer $[\mathrm{x}]=$ Greatest integer less than or equal to $x$ Some values of $[x]$ for specific values of $x$ $\begin{array}{l} {[3]=3} \\ {[4.4]=4} \\...
Show that function 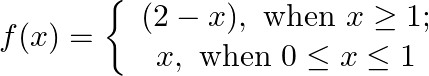 is continuous.
is continuous.
Solution: It is known that $\sin x$ is continuous everywhere Now considering the point $x=0$ L.H.L: $\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{-}}\left(\frac{\sin x}{x}\right)=\lim...
Show that sec 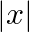 is a continuous function.
is a continuous function.
Solution: Assume $f(x)=\sec |x|$ and a be any real number. Then, L.H.L. at $\mathrm{x}=\mathrm{a}$ $\lim _{x \rightarrow \mathrm{a}^{-}} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow...
Show that sec  is a continuous function.
is a continuous function.
Solution: Assume $f(x)=\sec x$ So, $f(x)=\frac{1}{\cos x}$ $f(x)$ is not defined when $\cos x=0$ And $\cos x=0$ when, $x=\frac{\pi}{2}$ and odd multiples of $\frac{\pi}{2}$ like $-\frac{\pi}{2}$...
Show that function 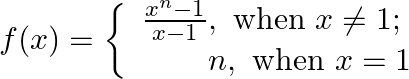
Solution: It is given that: $f(x)=\left\{\begin{array}{c} \frac{x^{n}-1}{x-1}, \text { when } x \neq 1 \\ n, \text { when } x=1 \end{array}\right.$ L.H.L. and $\mathrm{x}=1$ $\begin{array}{l} \lim...
Show that function 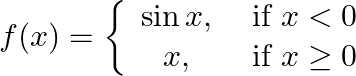 is continuous.
is continuous.
Solution: It is given that: $f(x)=\left\{\begin{array}{c} \sin x, \text { if } x<0 \\ x, \text { if } x \geq 0 \end{array}\right.$ L.H.L. at $\mathrm{x}=0$ $\lim _{x \rightarrow 0^{-}}...
Show that function 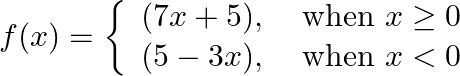 is continuous function.
is continuous function.
Solution: It is given that: $f(x)=\left\{\begin{array}{l} (7 x+5), \text { when } x \geq 0 \\ (5-3 x), \text { when } x<0 \end{array}\right.$ Let us now calculate the limit of $f(x)$ when $x$...
Prove that the function 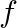 given
given 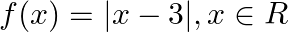 is continuous but not differentiable at
is continuous but not differentiable at 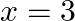
Solution: $f(x)=|x-3|$ As every modulus function is continuous for all real $x, f(x)$ is continuous at $x=3$. $f(x)=f(x)=\left\{\begin{array}{l} 3-x, x<0 \\ x-3, x \geq 0 \end{array}\right.$ In...
Find the values of a and b such that the following functions 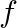 , defined as
, defined as  at
at 
Solution: $: \mathrm{f}$ is continuous at $x=0$ $\lim _{x \rightarrow 0-} f(x)=\lim _{x \rightarrow 0+} f(x)$ $\lim _{x \rightarrow 0-}\left(\operatorname{asin} \frac{\pi}{2}(x+1)\right)=\lim _{x...
Find the values of a and b such that the following functions continuous. 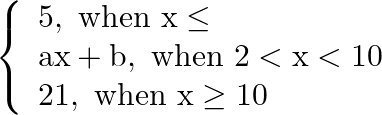
Solution: $f$ is continuous at $x=2$ $\begin{array}{l} \lim _{x \rightarrow 2-} f(x)=\lim _{x \rightarrow 2+} f(x)=f(2) \\ \lim _{x \rightarrow 2-}(5)=\lim _{x \rightarrow 2+}[a x+b]=5 \\...
Show that: 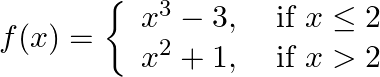 is continuous at
is continuous at 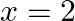
Solution: Left Hand Limit: $\lim _{x \rightarrow 2-} f(x)=\lim _{x \rightarrow 1-} x^{3}-3$ $=5$ Right Hand Limit: $\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{-}} x^{2}+1$ $=5$...
Show that: 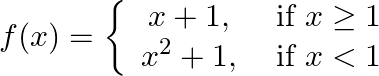 is continuous at
is continuous at 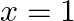
Solution: $\begin{array}{l} : \mathrm{Left Hand Limit}: \lim _{\mathrm{x} \rightarrow 1^{-}} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 1-} \mathrm{x}^{2}+1 \\ =2 \end{array}$...
Show that function: 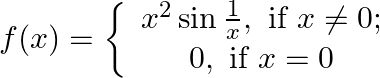
Solution: $\lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0} x^{2} \sin \frac{1}{x}$ As $\lim _{x \rightarrow 0} x^{2}=0$ and $\sin \left(\frac{1}{x}\right)$ is bounded function between $-1$ and...
For what valve of  is the following function
is the following function 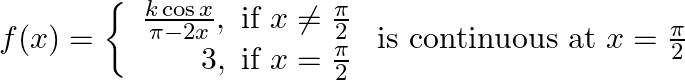 Ans.
Ans. 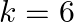
Solution: $f$ is continuous at $x=\frac{\pi}{2}$ $\begin{array}{l} \Rightarrow \lim _{x \rightarrow-\frac{\pi}{r}} f(x)=f\left(\frac{\pi}{2}\right) \\ \Rightarrow \lim _{x \rightarrow \frac{\pi}{r}}...
For what value of  is the following function
is the following function 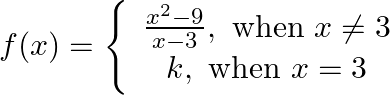 is continuous at
is continuous at 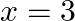 Ans.
Ans. 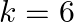
Solution: As, $f(x)$ is continuous at $x=3$ $\begin{array}{l} \Rightarrow \lim _{x \rightarrow 3} \frac{x^{2}-9}{x-3}=f(3) \\ \Rightarrow \lim _{x \rightarrow 3} \frac{(x-3)(x+3)}{x-3}=f(3) \\...
For what value of  is the following function continuous at
is the following function continuous at 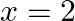
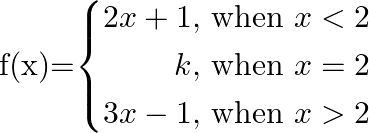
Solution: As, $f(x)$ is continuous at $x=2$ $\begin{array}{l} \Rightarrow \lim _{x \rightarrow 2-} 2 x+1=\lim _{x \rightarrow 2^{*}} 3 x-1=f(2) \\ \Rightarrow \lim _{x \rightarrow 2^{-}} 2 x+1=f(2)...
Find the value of 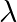 for which
for which 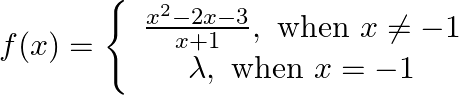
; is continuous at x=-1
Solution: As, $f(x)$ is continuous at $x=0$ $\begin{array}{l} \Rightarrow \lim _{x \rightarrow-1} \frac{x^{2}-2 x-3}{x+1}=f(0) \\ \Rightarrow \lim _{x \rightarrow-1} \frac{(x-3)(x+1)}{x+1}=\lambda...
Find the value of  for which
for which 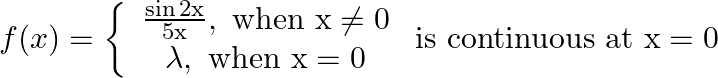
Solution: As, $f(x)$ is continuous at $x=0$ $\begin{array}{l} \Rightarrow \lim _{x \rightarrow 0} \frac{\sin 2 \mathrm{x}}{5 \mathrm{x}}=\mathrm{f}(0) \\ \Rightarrow \frac{1}{5} \lim _{\mathrm{x}...
Prove that 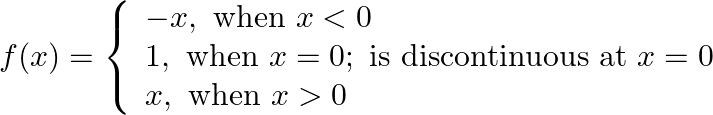
Solution: $\begin{array}{l} \text { Left Hand Limit: } \lim _{x \rightarrow 0-} f(x)=-x \\ =0 \end{array}$ Right Hand Limit: $\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2 *} x$ $=0$...
Prove that 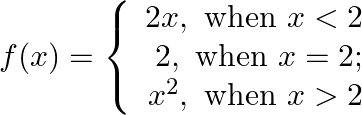
is discontinuous at x=2
Solution: Left Hand Limit: $\lim _{\mathrm{x} \rightarrow 2-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 2^{-}} 2 \mathrm{x}$ $=4$ Right Hand Limit: $\lim _{\mathrm{x} \rightarrow 2^{-}}...
Prove that 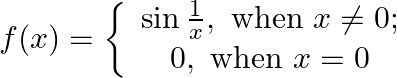
Solution: $\lim _{x \rightarrow 0} \sin \frac{1}{x}=0$ $\sin _{\mathrm{x}}^{1}$ is bounded function between $-1$ and $+1$ Also, $f(0)=0$ As, $\lim _{x \rightarrow 0} f(x)=f(0)$ As a result,...
Prove that 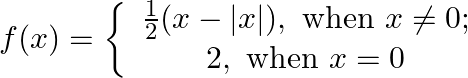 is discontinuous at x=0
is discontinuous at x=0
Solution: Left Hand Limit: $\lim _{\mathrm{x} \rightarrow 0-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 0-2} \frac{1}{2}(\mathrm{x}-|\mathrm{x}|)$ $=\lim _{x \rightarrow 0-2}...
Prove that 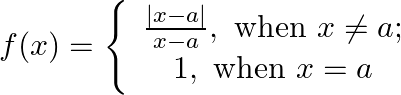
Solution: Left Hand Limit: $\lim _{\mathrm{x} \rightarrow \mathrm{a}-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow \mathrm{a}-} \frac{|\mathrm{x}-\mathrm{a}|}{\mathrm{x}-\mathrm{a}}$ $=\lim...
Prove that 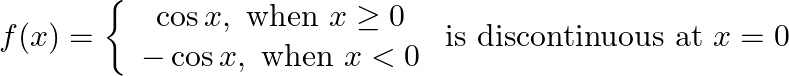
Solution: $\begin{array}{l} \text { Left Hand Limit: } \lim _{x \rightarrow 0-} f(x)=\lim _{x \rightarrow 0-} \cos x \\ =1 \end{array}$ Right Hand Limit: $\lim _{\mathrm{x} \rightarrow 0_{-}}...
Prove that 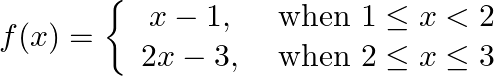 is continuous at
is continuous at 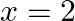
Solution: Left Hand Limit: $\lim _{\mathrm{x} \rightarrow 2-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 2^{-}} \mathrm{x}-1$ $=1$ Right Hand Limit: $\lim _{x \rightarrow 2^{-}} f(x)=\lim...
Prove that 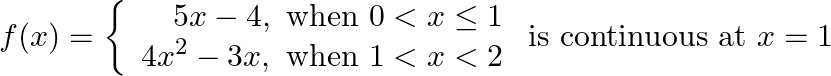
Solution: $\begin{array}{l} \text { Left Hand Limit: } \lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1-} 5 x-4 \\ =1 \end{array}$ Right Hand Limit: $\lim _{\mathrm{x} \rightarrow 1^{*}}...
Prove that 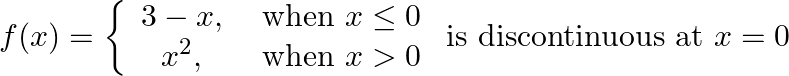
Solution: $\begin{array}{l} \text { Left Hand Limit: } \lim _{x \rightarrow 0-} f(x)=\lim _{x \rightarrow 0-} 3-x \\ =3 \end{array}$ $\begin{array}{l} \text { Right Hand Limit: } \lim _{x...
Prove that 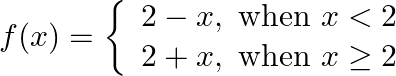 is discontinuous at
is discontinuous at 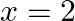
Solution : Left Hand Limit: $\lim _{\mathrm{x} \rightarrow 2-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 2-} 2+\mathrm{x}$ $=4$ Right Hand Limit: $\lim _{x \rightarrow 2^{-}} f(x)=\lim...
Prove that 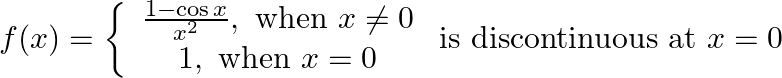
Solution: $\begin{array}{l} \text { Left Hand Limit: } \lim _{x \rightarrow 0-} f(x)=\lim _{x \rightarrow 0-} \frac{1-\operatorname{cosx}}{x^{2}} \\ =\lim _{x \rightarrow 0-} \frac{2 \sin ^{2}...
Prove that 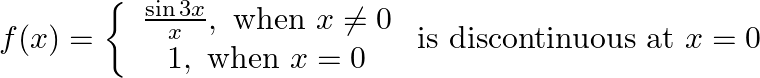
Solution: Left Hand Limit: $\lim _{\mathrm{x} \rightarrow 0-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 0-} \frac{\sin 3 \mathrm{x}}{\mathrm{x}}$ $=3$ $\left[\lim _{x \rightarrow a}...
Prove that 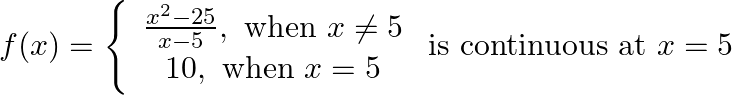
Solution: Left Hand Limit: $\lim _{x \rightarrow 5-} f(x)=\lim _{x \rightarrow 5-} \frac{x^{2}-25}{x-5}$ $=\lim _{x \rightarrow 5-} \frac{(x+5)(x-5)}{x-5}$ [By middle term splitting]...
Prove that 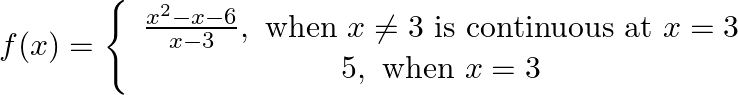
Solution: Left Hand Limit: $\lim _{x \rightarrow 3-} f(x)=\lim _{x \rightarrow 3-} \frac{x^{2}-x-6}{x-3}$ $=\lim _{\mathrm{x} \rightarrow 3-} \frac{(\mathrm{x}+2)(\mathrm{x}-3)}{\mathrm{x}-3}$ [By...
Show that 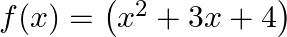 is continuous at
is continuous at 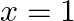
Solution: L.H.L.: $\lim _{\mathrm{x} \rightarrow 1-} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 1^{-}} \mathrm{x}^{2}+3 \mathrm{x}+4$ $=7$ R.H.L.: $\lim _{x \rightarrow 1^{-}} f(x)=\lim...
Show that 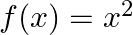 is continues at
is continues at 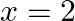
Solution: L.H.L.: $\lim _{x \rightarrow 2-} f(x)=\lim _{x \rightarrow 2-} x^{2}$ $=4$ R.H.L.: $\lim _{\mathrm{x} \rightarrow 2^{*}} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 2^{*}}...
Verify Mean Value Theorem if 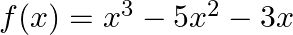 in the interval
in the interval ![Rendered by QuickLaTeX.com [a, b]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-63a0ed19b0a8ee859f2a1feb04156252_l3.png) where
where 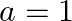 and
and 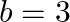 . Find all
. Find all 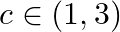 for which
for which 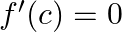 .
.
Solution: (a) Function is a polynomial as polynomial function is always continuous. As a result,it is continuous in $[1,3]$ (b) $f^{\prime}(x)=3 x^{2}-10 x_{5} f^{\prime}(x)$ exists in $[1,3]$, as a...

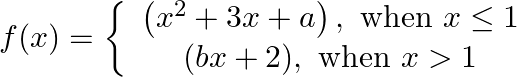 is differentiable at each
is differentiable at each