Let $I=\int _{\pi /6}^{\pi /2}\frac{\cos ecx\cot x}{1+\cos e{{c}^{2}}x}dx=\int _{\pi /6}^{\pi /2}\frac{\cos x}{1+{{\sin }^{2}}x}dx$ Let $\sin x=t$ $\Rightarrow \cos xdx=dt$ Also, when...
Let $I=\int _{1}^{2}\frac{1}{x{{(1+{{\log }_{e}}x)}^{2}}}dx$ Let $1+{{\log }_{e}}x=t$ $\Rightarrow \frac{1}{x}dx=dt$ Also, when $x=1,t=1$and when $x=2$ $t=1+{{\log }_{e}}2$ Hence, $I=\int...
Let $I=\int _{0}^{{{\left( \frac{\pi }{2} \right)}^{\frac{1}{3}}}}{{x}^{2}}\sin \left( {{x}^{3}} \right)dx$ Let ${{x}^{3}}=t$ $\Rightarrow 3{{x}^{2}}=dt$ Also, when $x=0,t=0$and when $t=\frac{\pi...
Let $I=\int _{\pi /4}^{\pi /2}\frac{\cos x}{{{\left( \cos \left( \frac{x}{2} \right)+\sin \left( \frac{x}{2} \right) \right)}^{3}}}dx$ $\cos x={{\cos }^{2}}\left( \frac{x}{2} \right)-{{\sin...
Let $I=\int _{2}^{3}\frac{2-x}{\sqrt{5x-6-{{x}^{2}}}}dx$ Let $2-x=\frac{ad}{dx}\left( 5x-6-{{x}^{2}} \right)+b$ $=-2ax+5a+b$ Hence $-2a=-1$and $5a+b=2$ Solving these equations, We get and...
Let $I=\int _{0}^{\pi /2}\left( \sqrt{\tan x}+\sqrt{\cos tx} \right)dx=\int _{0}^{\pi /2}\frac{\sin x+\cos x}{\sqrt{\sin x\cos x}}dx$ Let $\sin x-\cos x=t$ $\Rightarrow \left( \cos x+\sin x...
Let $I=\int _{0}^{1}\frac{1-{{x}^{2}}}{{{(1+{{x}^{2}})}^{2}}}dx$ Let $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ Also, when $x=0,t=0$and when $x=1,t=\frac{\pi }{4}$ Hence, $I'=\int _{0}^{\pi...
Let $I=\int _{0}^{1}{{x}^{3}}\sqrt{1+3{{x}^{4}}}dx$ Let $1+3{{x}^{4}}=t$ $\Rightarrow 12{{x}^{3}}dx=dt$ Also, when $x=0,t=1$and when $x=1,t=4$ $I=\frac{1}{12}\int _{1}^{4}\sqrt{t}dt$...
Let $I=\int _{0}^{9}\frac{1}{1+\sqrt{x}}$ Let $\sqrt{x}=u$ $\Rightarrow \frac{1}{2\sqrt{x}}=dx=du$ Or $dx=2udu$ $=\frac{1}{2u}dx$ Also, when $x=0,u=0$and $x=9,u=3$ Hence, $I=\int...
Let $I=\int _{0}^{a}{{\sin }^{-1}}\sqrt{\frac{x}{a+x}}dx$ Let $x=a{{\tan }^{2}}y$ $\Rightarrow dx=2a\tan y{{\sec }^{2}}ydy$ Also, when $x=0,y=0$ And when $x=a$ $y=\frac{\pi }{4}$ Hence, $I=\int...
Let $I=\int _{0}^{1}{{\sin }^{-1}}\sqrt{x}dx$ Let $\sqrt{x}=1$ $\Rightarrow \frac{1}{2\sqrt{x}}=dx=dt$ Or $dx=2tdt$ When $x=0,t=0$ And when $x=1,t=1$ Hence, $I=2\int _{0}^{1}t{{\sin }^{-1}}tdt$...
Let $I=\int _{0}^{1}x{{(a{{\tan }^{-1}}x)}^{2}}dx$ Using integration by parts, we get $I=\frac{{{\left( {{\tan }^{-1}}x \right)}^{2}}{{x}^{2}}}{2}|_{0}^{1}-\int _{0}^{1}\frac{2{{\tan...
Let $I=\int _{0}^{1}{{\left( {{\cos }^{-1}}x \right)}^{2}}dx$ Let $x=\cos t\Rightarrow dx=-\sin tdt$ Also, when $x=0,t=\frac{\pi }{2}$ And when $x=1,t=0$ Hence, $I=-\int _{\pi /2}^{0}{{t}^{2}}\sin...
Let \[I=\int _{\pi /3}^{\pi /2}\frac{\sqrt{1+\cos x}}{(1-\cos x)\frac{5}{2}}dx\] Using $1+\cos x=2\cos {{x}^{2}}\left( \frac{x}{2} \right)$ $1-\cos x=2{{\sin }^{2}}\left( \frac{x}{2} \right)$ we get...
Let $I=\int _{0}^{\pi /2}\frac{\sin 2x}{{{\sin }^{4}}x+{{\cos }^{4}}x}dx$ Using $\sin 2x=2\sin x\cos x$, we get $=2\int _{0}^{\pi /2}\frac{\tan x{{\sec }^{2}}x}{({{\tan }^{4}}x+1)}dx$ $I=\int...
Let $I=\int _{0}^{\pi /2}\frac{\sin x\cos x}{{{\cos }^{2}}x+3\cos x+2}dx$ Let $\cos x=t$ $\Rightarrow -\sin xdx=dt$ Also, when $x=0,t=1$ And when $t=0$ $x=\frac{\pi }{2}$ Hence, $I=-\int...
Let $I=\int _{0}^{\pi /4}\frac{{{\tan }^{3}}x}{1+\cos 2x}dx$ Using $1+\cos 2x=2{{\cos }^{2}}x$, we get $I=\frac{1}{2}\int _{0}^{\pi /4}{{\tan }^{3}}x{{\sec }^{2}}xdx$ Let $\tan x=t$ $\Rightarrow...
Let $I=\int _{0}^{\pi }\frac{1}{3+\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2}...
$f(x)$is continuous in $\left[ a,b \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=\left( b-a \right)/n$ $\int...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{1}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
Since it is modulus function so we need to break the function and then solve it $f\left( x \right)=\int _{0}^{1/3}\left( 1-3x \right)dx+\int _{1/3}^{1}(3x-1)dx$it is continuous in $\left[ 0,1...
$f\left( x \right)$is continuous in $\left[ 0,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ $\int _{0}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
$f(x)$is continuous in $\left[ 2,4 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ And $\cos x=\frac{1-{{\tan...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ And $\cos x=\frac{1-{{\tan...
Let $I=\int{_{0}^{\pi }}\frac{1}{5+4\cos x}dx$ Using, we get $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $I=\int{_{0}^{\pi...
$I=\int{_{0}^{\pi }}\frac{1}{6-\cos x}dx$ Using, we get $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $I=\int{_{0}^{\pi }}\frac{1-{{\tan...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{5+4\sin x}dx$ $$$\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{4+9{{\cos }^{2}}x}dx$ Dividing by ${{\cos }^{2}}x$ in numerator and denominator, we get $$$I=\int{_{0}^{\frac{\pi }{2}}}\frac{{{\sec }^{2}}x}{2{{\sec...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{1+{{\cos }^{2}}x}dx$ Dividing by ${{\cos }^{2}}x$in numerator and denominator, we get $I=\int{_{0}^{\frac{\pi }{2}}}\frac{{{\sec...
Let $I=\int{_{0}^{\frac{\pi }{2}}\frac{1}{{{a}^{2}}{{\cos }^{2}}x+{{b}^{2}}{{\sin }^{2}}x}dx}$ Dividing by ${{\cos }^{2}}x$in numerator and denominator, we get $I=\int{_{0}^{\frac{\pi...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{1+\sin x}dx$ Using and ${{\sin }^{2}}\frac{x}{2}+\cos \frac{x}{2}=1$ $\sin x=2\sin \frac{x}{2}\cos \frac{x}{2}$ $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{{{\left(...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{1+\cos x}dx$ Using, we get $1+\cos x=2{{\cos }^{2}}\frac{x}{2}$ $I=\sqrt{2\sin }\left( \frac{x}{2} \right)\left| _{0}^{\frac{\pi }{2}} \right.=2$
Let $I=\int{_{0}^{1}}{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)dx$ Let $\int{\left( x \right)}={{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)$ Let $x=\tan \theta $ $\Rightarrow \theta...
Let $I=\int{_{0}^{2}x\sqrt{2-xdx}}$ Using the property that, we get $\int{_{a}^{b}f(x)dx=\int{_{a}^{b}f(a+b-x)dx}}$ $I=\int{_{0}^{2}(2-x)\sqrt{xdx}}$...
Let $I=\int{_{0}^{1}\frac{x}{\sqrt{{{a}^{2}}+{{x}^{2}}}}dx}$ Let ${{a}^{2}}+{{x}^{2}}={{t}^{2}}$ $\Rightarrow xdx=tdt.$ Also when $x=0,t=a$ And when x=a, $t=\sqrt{2a}$ Hence ,...
Let $I=\int{_{0}^{a}\frac{{{x}^{4}}}{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx}$ Let x=a sin t a cos t dt=dx also, when $x=0,t=0$ and when x=a , $t=\frac{\pi }{2}$ Hence, $I=\int{_{0}^{\frac{\pi...
Let $I=\int{_{0}^{\sqrt{2}}\sqrt{2-{{x}^{2}}}dx}$ Consider, $I=\int{_{0}^{\sqrt{2}}\sqrt{2-{{x}^{2}}}dx}$ Let x=a sin t $\Rightarrow a\cos ttdt=dx$ Also, when $x=0,t=0$ and when x=a, $t=\frac{\pi...
Let $I=\int{_{0}^{a}\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$ Let x=a sin t $\Rightarrow a\cos tdt=dx$ Also, $x=0,t=0$ And When $x=a,t=\frac{\pi }{2}$ Hence, $I=\int{_{0}^{\frac{\pi...
$I=\int{_{0}^{\frac{\pi }{2}}\frac{\sin x\cos x}{1+{{\sin }^{4}}x}dx}$ Let ${{\sin }^{2}}x=t$ $\Rightarrow 2\sin x\cos x=dt.$ Also, When $x=0,t=0$ And When $x=\frac{\pi }{2},t=1.$ Hence,...
Let $I=\int{_{0}^{\frac{\pi }{2}}\sqrt{\sin x{{\cos }^{5}}xdx}}$ Let $\sin x=t$ $\Rightarrow \cos xdx=dt.$ Also, When $x=0,t=0$ And When $x=\frac{\pi }{2},t=1.$ Consider ${{\cos }^{5}}x={{\cos...
Let $I=\int{_{0}^{\frac{\pi }{2}}\frac{\sin x}{\sqrt{1+\cos x}}dx}$ Let $1+cosx=t$ $\Rightarrow -\sin xdx=dt.$ Also, when $x=0,t=2$ And When $x=\frac{\pi }{2},t=1$ Hence,...
Let $I=\int{_{0}^{1}}\sqrt{\frac{{{\tan }^{-1}}x}{1+{{x}^{2}}}dx}$ Let ${{\tan }^{-1}}x=t$ $\Rightarrow \frac{1}{1+{{x}^{2}}}dx=dt$ When $x=1$, $t=\frac{\pi }{4}$ Hence, $I=\int{_{0}^{\frac{\pi...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ $\int _{1}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\left[ 2,5 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=\left( b-a \right)/n$ Here $h=3/n$ $\int...
$f(x)$is continuous in $\left[ 2,5 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+r-h)$, where $h=(b-a)/n$ Here $h=3/n$ $\int...
$f(x)$is continuous in $\left[ 0,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=b-a/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=\left( b-a \right)/n$ Here $h=2/n$ $\int...
$f(x)$is continuous in $\left[ 1,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=1/n$ $\int...
$f(x)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2n$ $\int _{0}^{2}\left( x+4...
$y=\int _{0}^{4}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx$ $y=\int _{0}^{2}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx+\int _{2}^{4}\left| x \right|+\left| x-2...
$y=\int _{0}^{4}f(x)dx$ $y=\int _{0}^{2}f(x)dx+\int _{2}^{4}f(x)dx$ $y=\int _{0}^{2}3{{x}^{2}}+4dx+\int _{2}^{4}9x-2dx$ $y=\left( {{x}^{3}}+4x \right)_{0}^{2}+\left( \frac{9{{x}^{2}}}{2}-2x...
$y=\int _{1}^{3}f(x)dx$ $y=\int _{1}^{2}f(x)dx+\int _{2}^{3}f(x)dx$ $y=\int _{1}^{2}2x+1dx+\int _{2}^{3}{{x}^{2}}+1dx$ $y=\left( {{x}^{2}}+x \right)_{1}^{2}+\left( \frac{{{x}^{3}}}{3}+x...
We know that $\left| \sin x \right|=-\sin x$in $\left[ -\pi /4,0 \right)$ $\left| \sin x \right|=\sin x$in $\left[ 0,\pi /4 \right]$ $y=\int _{-\pi /4}^{0}\left| \sin x \right|dx+\int _{0}^{\pi...
We know that $\left| \cos x \right|=\cos x$in $\left[ 0,\pi /2 \right)$ $\left| \cos x \right|=-\cos x$in $\left[ \pi /2,3\pi /2 \right)$ $\left| \cos x \right|=\cos x$in $\left[ 3\pi /2,2\pi ...
We know that $\left| x-5 \right|=-(x-5)$in $\left[ 0,5 \right)$ $\left| x-5 \right|=(x-5)$in $\left[ 5,8 \right]$ $y=\int _{0}^{5}\left| x-5 \right|dx+\int _{5}^{8}\left| x-5 \right|dx$ $y=\int...
We know that $\left| x+1 \right|=-(x+1)$in $\left[ -2,-1 \right)$ $\left| x+1 \right|=(x+1)$in $\left[ -1,2 \right]$ $y=\int _{-2}^{-1}\left| x+1 \right|dx+\int _{-1}^{2}\left| x+1 \right|dx$...
We know that $\left| x \right|=-x$in $\left[ -1,0 \right)$ $\left| x \right|=x$in $\left[ 0,1 \right]$ $y=\int _{-1}^{0}{{e}^{\left| x \right|}}dx+\int _{0}^{1}{{e}^{\left| x \right|}}dx$ $y=\int...
$y=\int _{-\pi }^{\pi }{{x}^{12}}{{\sin }^{9}}xdx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\left( \pi -\pi -x...
$y=\int _{-\pi }^{\pi }{{\sin }^{75}}x+{{x}^{125}}dx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\sin }^{75}}\left( \pi -\pi...
$y=\int _{-a}^{a}{{x}^{3}}\sqrt{{{a}^{2}}-{{x}^{2}}dx}.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int...
Let $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ At $x=0,t=0$ At $x=1,t=\pi /4$ \[y=\int _{0}^{\pi /4}\frac{\log \left( 1+\tan t \right)}{1+{{\tan }^{2}}t}{{\sec }^{2}}tdt\] \[y=\int _{0}^{\pi...
Use integration by parts $\int I\times IIdt=I\int IIdt-\int \frac{d}{dt}I\left( \int IIdt \right)dt$ $y=\log x\int \frac{\sqrt{1}}{\sqrt{1-{{x}^{2}}}}dx-\int \frac{d}{dx}\log x\left( \int...
Let, $x=\sin t$ $\Rightarrow dx=\cos tdt$ At $x=0,t=0$ At $x=1,t=\pi /2$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{-1}}\sin t}{\sin t}\cos tdt$ $y=\int _{0}^{\pi /2}\frac{t\cos t}{\sin t}dt$ $y=\int...
Use integration by parts $\int I\times IIdx=I\int IIdx-\int \frac{d}{dx}I\left( \int IIdx \right)dx$ $y=x\int \cot xdx-\int \frac{d}{dx}x\left( \int \cot xdx \right)dx$ $y=\left( x\log \sin x...
Use king theorem of definite integral $\int _{a}^{b}f(x)=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{1}^{4}\frac{\sqrt{4+1-x}}{\sqrt{4+1-x}+\sqrt{x}}dx$ $y=\int...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{a/4}^{3a/4}\frac{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}}{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}+\sqrt{x}}dx$...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /4}^{3\pi /4}\frac{\left( \frac{3\pi }{4}+\frac{\pi }{4}-x \right)}{1+\sin \left( \frac{3\pi...
$y=\frac{1}{2}\int _{\pi /4}^{3\pi /4}{{\sec }^{2}}\frac{x}{2}dx$ $y=\frac{1}{2}\left( \frac{\frac{\tan x}{2}}{\frac{1}{2}} \right)_{\pi /4}^{3\pi /4}$ $y=\tan \frac{3\pi }{8}-\tan \frac{\pi }{8}$...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /6}^{\pi /3}\frac{\sqrt{\cos \left( \frac{\pi }{3}+\frac{\pi }{6}-x \right)}}{\left( \sqrt{\sin...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /8}^{3\pi /8}\frac{\cos \left( \frac{3\pi }{8}+\frac{\pi }{8}-x \right)}{\sin \left( \frac{3\pi...
![Rendered by QuickLaTeX.com \[y=\int _{0}^{\pi /2}\log \left( \frac{\sin x}{\cos x}+\frac{\cos x}{\sin x} \right)dx\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a679411f8191078aadb81574c6f2b9f5_l3.png)
\[y=\int _{0}^{\pi /2}\log \frac{1}{\sin x\cos x}dx\] \[y=-\left( \int _{0}^{\pi /2}\log \sin xdx+\int _{0}^{\pi /2}\log \cos xdx \right)\] Let, $I=\int _{0}^{\pi /2}\log \sin xdx......(1)$ Use king...
Use king theorem of definite integral \[\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx\] \[y=\int _{0}^{\pi }\log (1+\cos (\pi -x))dx\] \[y=\int _{0}^{\pi }\log (1-\cos x)dx........(2)\] Adding...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\left( \pi -x \right)\log \sin \left( \pi -x \right)dx$ $y=\int _{0}^{\pi }\pi \log \sin...
$y=\int _{0}^{\pi /2}\log 2+\log \sin x+\log \cos xdx$ Let, $I=\int _{0}^{\pi /2}\log \sin xdx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)$ $I=\int...
Let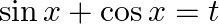
$\Rightarrow \cos x-\sin xdx=dt$ At $x=0,t=1$ At $x=\pi /2,t=1$ $y=\int _{1}^{1}-\log tdt$ We know that when upper and lower limit in definite integral is equal then value of integration is zero....
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }{{\sin }^{2m}}\left( \pi -x \right){{\cos }^{2m+1}}\left( \pi -x \right)dx$ $y=-\int _{0}^{\pi...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }{{\sin }^{2}}\left( \pi -x \right){{\cos }^{3}}\left( \pi -x \right)dx$ $y=-\int _{0}^{\pi...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{a}\frac{\sqrt{a-x}}{\sqrt{a-x}+\sqrt{x}}dx.......(2)$ Adding equation (1) and (2) $2y=\int...
Let 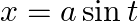
$\Rightarrow dx=a\cos tdt$ At $x=0,t=0$ At $x=a,t=0$ $y=\int _{0}^{\pi /2}\frac{a\cos t}{a\sin t+\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}t}}dt$ $y=\int _{0}^{\pi /2}\frac{\cos t}{\sin t+\cos t}dt$...
Let, $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ At $x=0,t=0$ At $x=\infty ,t=\pi /2$ $y=\int _{0}^{\pi /2}\frac{\tan t}{(1+\tan t)(1+{{\tan }^{2}}t)}{{\sec }^{2}}tdt$ $y=\int _{0}^{\pi...
$y=\int _{0}^{\pi /2}\log \frac{{{\cos }^{2}}x}{2\sin x\cos x}dx$ $y=\int _{0}^{\pi /2}\log \left( \frac{1}{2}\cot x \right)dx.....(1)$ Use king theorem of definite integral $\int...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)}{1+{{\sin }^{2}}\left( \pi -x \right)}dx$ $y=\int _{0}^{\pi...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\sin \left( \pi -x \right)}{1+\sin \left( \pi -x \right)}dx$ $y=\int...
$y=\int _{0}^{\pi }\frac{x\sin x}{1+{{\cos }^{2}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\sin...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{2}}\left( \frac{\pi }{2}-x \right)}{\sin \left( \frac{\pi }{2}-x \right)+\cos...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\tan \left( \pi -x \right)}{\sec \left( \pi -x \right)\cos ec\left(...
$\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{2}(2-x)\sqrt{x}dx$ $y=\int _{0}^{2}2{{x}^{\frac{1}{2}}}-{{x}^{\frac{1}{2}}}dx$ $y=\left(...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{1}(1-x){{x}^{5}}dx$ $y=\int _{0}^{1}{{x}^{5}}-{{x}^{6}}dx$ $y=\left(...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\sin \left( \frac{\pi }{2}-x \right)-\cos \left( \frac{\pi }{2}-x \right)}{1+\sin...
$y=\int _{0}^{\pi /2}\frac{\sqrt{\sin x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ \[y=\int...
$y=\int _{0}^{\pi /2}\frac{\sqrt{\cos x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...
Q15. $y=\int _{0}^{\pi /2}\frac{1+}{1+\sqrt{\frac{\sin x}{\cos x}}}dx$ $y=\int _{0}^{\pi /2}\frac{\sqrt{\cos x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx.....(1)$ Use king theorem of definite...
$y=\int _{0}^{\pi /2}\frac{{{\sin }^{3}}x}{{{\sin }^{3}}x+{{\cos }^{3}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...
$y=\int _{0}^{\pi /2}\frac{{{\cos }^{3}}x}{{{\sin }^{3}}x+{{\cos }^{3}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...
$y=\int _{0}^{\pi /2}\frac{\sin x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ \[y=\int _{0}^{\pi /2}\frac{\sin \left( \frac{\pi...
$y=\int _{0}^{\pi /2}\frac{\cos x}{\sin x+\cos x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\cos \left( \frac{\pi...
$y=\int _{0}^{\pi /2}\frac{\cos x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\cos \left( \frac{\pi...
$y=\int _{0}^{\pi /2}\frac{\sin x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\sin \left( \frac{\pi...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{n}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{n}}\left( \frac{\pi }{2}-x...
Use king theorem of definite integral \[\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx\] \[y=\int _{0}^{\pi /2}\frac{{{\sin }^{\frac{3}{2}}}\left( \frac{\pi }{2}-x \right)}{{{\sin...
Use king theorem definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{\frac{1}{4}}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{\frac{1}{4}}}\left(...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{4}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{4}}\left( \frac{\pi }{2}-x...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{4}}\left( \frac{\pi }{4}-x \right)}{{{\sin }^{4}}\left( \frac{\pi }{2}...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{7}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{7}}\left( \frac{\pi }{2}-x...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{3}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{3}}\left( \frac{\pi }{2}-x...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{b}^{\pi /2}\frac{{{\sin }^{3}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{3}}\left( \frac{\pi }{2}-x...
2. 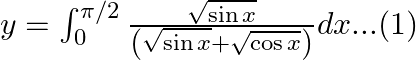
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\sqrt{\sin \left( \frac{\pi }{2}-x \right)}}{\left( \sqrt{\sin \left( \frac{\pi }{2}-x...
1. 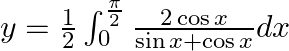
$=\frac{1}{2}\int _{0}^{\frac{\pi }{2}}\frac{\cos x+\cos x-\sin x+\sin x}{\sin x+\cos x}dx$ $=\frac{1}{2}\int _{0}^{\frac{\pi }{2}}1+\frac{\cos x-\sin x}{\sin x+\cos x}dx$ $=\frac{1}{2}\left( \left(...
Let $I=\int{_{\frac{1}{e}}^{e}\frac{1}{x\left( {{\log }_{e}}x \right)\frac{1}{3}}dx}$ $$let ${{\log }_{e}}x=t$ $\Rightarrow .$ $\Rightarrow \frac{1}{x}dx=dt$ When $t=-1$ $x=\frac{1}{e}$ And When,...
Let $I=\int \frac{1}{{{e}^{x}}+{{e}^{-x}}}dx=\int (\frac{{{e}^{x}}}{1+{{e}^{2x}}}dx\text{ )}$ Let ${{e}^{x}}=t$ $\Rightarrow {{e}^{x}}dx=dt.$ When $x=0,t=1$ And When $x=1,t=e.$ Hence,...
Let $\cos x=t$ $I=\int{_{0}^{\frac{\pi }{2}}}\frac{\sin x}{1+{{\cos }^{2x}}}dx$ Let $\cos x=t$ $\Rightarrow -\sin xdx=dt.$ When $x=0,t=1$ And When, $t=0.$ $x=\frac{\pi }{2}$ Hence,...
Let $I=\int{_{0}^{\frac{\pi }{6}}\frac{\cos x}{3+4\sin x}dx}$ Let $3+4\sin x=t$ $\Rightarrow 4\cos xdx=dt.$ When $x=0,t=3$ And When, $t=5.$ $x=\frac{\pi }{6}$ Hence,...
Let $I=\int{_{1}^{2}}\frac{e\frac{1}{x}}{{{x}^{2}}}dx$ Let $\frac{1}{x}=t$ $\Rightarrow .$ $\Rightarrow \frac{-1}{{{x}^{2}}}dx=dt$ when$x=1,t=1$ and when $x=2,.$ $t=\frac{1}{2}$ Hence,...
Let $I=\int{_{0}^{1}x{{e}^{x2}}dx}$ Let ${{x}^{2}}=t$ $\Rightarrow 2xdx=dt.$ Also, When $x=0,t=0$ And When $x=1,t=1.$ Hence, $I=\frac{1}{2}\int{_{0}^{1}}{{e}^{t}}dt$ $=\frac{1}{2}{{e}^{t}}\left|...
Let $I=\int{2x1+x410dx}$ Let ${{x}^{2}}=t$ $\Rightarrow 2xdx=dt.$ When $x=0,t=0$ And When $x=1,t=1$ Hence, $I=\int{_{0}^{1}}\frac{1}{1+{{t}^{2}}}dt$ $={{\tan }^{-1}}t\left| _{0}^{1} \right.$...
Let $I=\int{2x1+x410dx}$ Let ${{x}^{2}}=t$ $\Rightarrow 2xdx=dt.$ When $x=0,t=0$ And When $x=1,t=1$ Hence, $I=\int{_{0}^{1}}\frac{1}{1+{{t}^{2}}}dt$ $={{\tan }^{-1}}t\left| _{0}^{1} \right.$...
Let $I=\int{_{0}^{1}}\frac{{{e}^{x}}}{1+{{e}^{2x}}}dx$ Let ${{e}^{x}}=t$ $\Rightarrow {{e}^{x}}dx=dt.$ When $x=1,t=e.$ Hence, $I=\int{_{1}^{e}}\frac{1}{1+{{t}^{2}}}dt={{\tan }^{-1}}\left. t...
Let $I=\int{_{1}^{2}\frac{3x}{9{{x}^{2-1}}}dx}$ Let $9{{x}^{2}}-1=t$ $\Rightarrow 18xdx=dt.$ Also, When $x=2,t=35.$ Hence, $I=\frac{1}{6}\int{_{8}^{35}\frac{1}{t}dt=\frac{1}{6}{{\log }_{e}}t\left|...
Let $I=\int{_{1}^{2}\frac{3x}{9{{x}^{2-1}}}dx}$ Let $9{{x}^{2}}-1=t$ $\Rightarrow 18xdx=dt.$ Also, When $x=2,t=35.$ Hence, $I=\frac{1}{6}\int{_{8}^{35}\frac{1}{t}dt=\frac{1}{6}{{\log }_{e}}t\left|...
Let $I=\int{_{0}^{1}\frac{2X}{1+{{X}^{2}}}dx}$ $Let1+{{x}^{2}}=t$ $\Rightarrow 2xdx=dt.$ When $x=1,t=2$ Hence, $I=\int{_{1}^{2}\frac{1}{t}dt={{\log }_{e}}1}$ $={{\log }_{e}}2-{{\log }_{e}}1$...
Let $I=\int{_{0}^{1}\frac{1}{2x-3}dx}$ $let2x-3=t$ $\Rightarrow 2dx=dt$ Hence, $I=\frac{1}{2}\int{_{0}^{1}\frac{1}{t}dt=\frac{1}{2}}{{\log }_{e}}\left| t \right|$ $=\frac{1}{2}{{\log }_{e}}\left|...
. 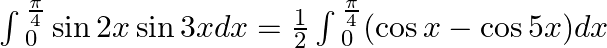
$=\frac{1}{2}\int{_{0}^{\frac{\pi }{4}}(cox-\cos 5x)dx}$ $=\frac{1}{2}\left[ \sin x-\frac{\sin 5x}{5} \right]$ $=\frac{1}{2}\left[ \sin \left( \frac{\pi }{4} \right)-\frac{\sin \left( \frac{5\pi...
$\int{_{\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{dx}{2{{\sin }^{2}}x}=\int{_{\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{1}{2}\frac{dx}{2}\cos e{{c}^{2}}xdx}}$ $\int{_{\frac{\pi }{2}}^{\frac{\pi...
$\int{_{0}^{\frac{\pi }{4}}\frac{dx}{1+\cos 2x}=\int{_{0}^{\frac{\pi }{4}}\frac{1}{2}{{\sec }^{2}}xdx}}$ $\int{_{0}^{\frac{\pi }{4}}\frac{1}{2}{{\sec }^{2}}xdx=\frac{1}{2}[\tan x]}$...
Let $u=\left( \tan \left( \frac{x}{2} \right)+1 \right)$ $dx=\frac{2}{{{\sec }^{2}}\left( \frac{x}{2} \right)}du$ $=-\frac{2}{u}$ $=-\frac{2}{\tan \left( \frac{x}{2} \right)+1}$ $=2$
$\int{_{0}^{\frac{\pi }{4}}(\cos x-\sin x)dx}$ $=[\sin x+\cos x]$ $=\left[ \cos \left( \frac{\pi }{4} \right)+\sin \left( \frac{\pi }{4} \right)-\cos 0-\sin 0 \right]$ $=\left[...
. 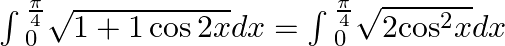
$=\sqrt{2}\left| \sin x \right|$ $\sqrt{2}\left| \sin \left( \frac{\pi }{4} \right)-\sin 0 \right|$ $\sqrt{2}\left[ \frac{1}{\sqrt{2}} \right]$ $=1$
$\frac{1}{4}\int{_{0}^{\frac{\pi }{2}}(3\sin x-\sin 3x)dx=\frac{1}{4}\left[ -3\cos x+\frac{\cos 3x}{3} \right]}$ $=\frac{1}{4}\left[ -3\cos \left( \frac{\pi }{2} \right)+\frac{\cos \left( \frac{3\pi...
$\frac{1}{4}\int{_{0}^{\frac{\pi }{3}}(3\cos x-\cos 3x)dx=\frac{1}{4}\left[ 3\sin x+\frac{\sin 3x}{3} \right]}$ $\frac{1}{4}\left[ 3\sin \left( \frac{\pi }{3} \right)+\frac{\sin \pi }{3}...
$=-\log \left| \cos ec\left( \frac{\pi }{4} \right)+\cot \left( \frac{\pi }{4} \right) \right|+\log \left| \cos ec\left( \frac{\pi }{6} \right)+\cot \left( \frac{\pi }{6} \right) \right|$ $=-\log...
$=2\log (2)-(2)-1\log (1)+(1)$ $=2\log (2)-1$
$=\int{_{0}^{\frac{\pi }{2}}\frac{{{x}^{2}}}{2}(\cos (2x)+\frac{{{x}^{2}}}{2})dx}$ $\int{_{0}^{\frac{\pi }{2}}\frac{{{x}^{2}}}{2}(\cos (2x)+\frac{{{x}^{2}}}{2})dx}=\frac{{{x}^{2}}\sin...
$=-\frac{{{x}^{3}}\cos (3x)}{3}+\frac{{{x}^{2}}\sin (3x)}{3}-\int{\frac{2x\sin x(3x)}{3}dx}$ $=-\frac{{{x}^{3}}\cos (3x)}{3}+\frac{{{x}^{2}}\sin (3x)}{3}+\frac{2x\cos (3x)}{9}-\frac{2\sin (3x)}{27}$...
$\int{_{0}^{\frac{\pi }{2}}{{x}^{2}}\sin (2x)dx=\left[ \frac{{{x}^{2}}\sin (2x)}{2}-\frac{\sin (2x)}{2}+\frac{x\cos (2x)}{2} \right]}$ $\left[ \frac{{{\left( \frac{\pi }{2} \right)}^{2}}\sin (\pi...
From integrate by parts: 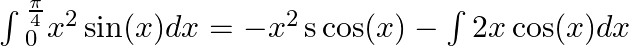
From integrate by parts: $\int{_{0}^{\frac{\pi }{4}}{{x}^{2}}\sin (x)dx=[-{{x}^{2}}\cos (x)+2\sin (x)+2\cos (x)]}$ $=[2x\sin (x)+(2-{{x}^{2}})\cos (x)]$ $=\left[ \frac{\pi }{2}\sin \left( \frac{\pi...
$$$\int{_{0}^{\frac{\pi }{2}}{{x}^{2}}\cos (x)dx=[{{x}^{2}}\sin (x)-2x\cos (x)]}$ $=\left[ {{\left( \frac{\pi }{4} \right)}^{2}}\sin \left( \frac{\pi }{2} \right)-2\sin \left( \frac{\pi }{2}...
$=[(x-1){{e}^{x}}]$ $=[(1-1){{e}^{1}}-(0-1){{e}^{0}}]$ $=1$
.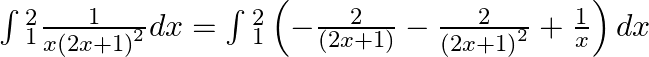
$=-2\int{_{1}^{2}\frac{1}{2x+1}dx-2=\int{_{1}^{2}\frac{1}{{{(2x+1)}^{2}}}dx+\int{_{1}^{2}\frac{1}{x}dx}}}$ $=-2\left[ \frac{1}{2}\log (2x+1) \right]-2\left[ \frac{-1}{2(2x+1)} \right]+[\log (x)]$...
Perform partial fraction decomposition: $\int{_{1}^{3}\frac{1}{{{x}^{2}}(x+1)}dx}=\int{_{1}^{3}\left( \frac{1}{x+1}-\frac{1}{x}+\frac{1}{{{x}^{2}}} \right)dx}$ $=[\log (x+1)-\log (x)-\frac{1}{x}]$...
$=\frac{1}{2}\int{_{0}^{1}\sqrt{1-{{(2x-1)}^{2}}}dx}$ Substitute: $2x-1=u$ $\therefore dx=\frac{1}{2}du$ $\therefore \frac{1}{2}\int{\sqrt{1-{{u}^{2}}}du}$ Substitute: U=sin(v) $\therefore {{\sin...
$\int{_{\frac{1}{4}}^{\frac{1}{2}}\frac{dx}{\sqrt{x-{{x}^{2}}}}=\int{_{\frac{1}{4}}^{\frac{1}{2}}\frac{1}{\sqrt{\frac{1}{4}-{{\left( x-\frac{1}{2} \right)}^{2}}}}}}$ Substitute: $2x-1=u$ $\therefore...
Assume that 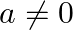
$\int{_{0}^{2}\frac{1}{-{{x}^{2}}+ax+{{a}^{2}}}dx=-\int{_{0}^{2}\frac{1}{{{x}^{2}}-ax-{{a}^{2}}}dx}}$ $\int{_{0}^{2}\frac{4}{(2x+(-\sqrt{5}-1)a)(2x+\sqrt{5}-1)a)}dx}$...
By reduction formula: ![Rendered by QuickLaTeX.com \int{{{\cos }^{2}}xdx=\frac{1}{2}\left[ \frac{\sin 2x}{2}+x \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b65244f8b3b3839e19b52a41514f6aa2_l3.png)
$\int{_{0}^{\frac{\pi }{2}}{{\cos }^{4}}xdx=\frac{{{\cos }^{3}}(x)\sin (x)}{4}+\frac{3}{8}\left[ \frac{\sin 2x}{2}+x \right]}$ $=\frac{{{\cos }^{3}}\left( \frac{\pi }{2} \right)\sin \left( \frac{\pi...
$\int{_{\frac{\pi }{3}}^{\frac{\pi }{4}}\left( \frac{{{\tan }^{2}}x+1}{\tan x} \right)dx=\int{_{\frac{\pi }{3}}^{\frac{\pi }{4}}\frac{{{\sec }^{2}}x({{\tan }^{2}}x+1)}{{{\tan }^{2}}x}dx}}$...
$=\left[ \frac{a}{2}\left( \frac{\sin \pi }{2}+\frac{\pi }{2} \right)+\frac{b}{2}\left( \frac{\pi }{2}-\frac{\sin \pi }{2} \right)-\frac{a}{2}\left( \frac{\sin 0}{2}+0 \right)-\frac{b}{2}\left(...
. 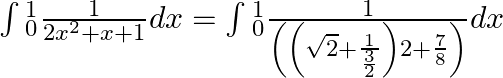
Substitute $4x+1\sqrt{7}=u$ $\therefore dx=\frac{\sqrt{7}}{4}du$ Now solving: $\int{\left( \frac{1}{{{u}^{2}}}+1 \right)du={{\tan }^{-1}}u}$ $\frac{2}{\sqrt{7}}\int{\left( \frac{1}{{{u}^{2}}+1}...
Substitute: $x+2=u$ $\therefore dx=du$ $=\int{\frac{du}{\sqrt{{{u}^{2}}-1}}}$ $=\log (\sqrt{{{u}^{2}}-1}+u$ Undo substitution: $x+2=u$ $\therefore \int{_{0}^{4}\frac{dx}{\sqrt{{{x}^{2}}+4x+3}}=\log...
Substitute: $\frac{x+1}{\sqrt{2}}=u$ $\therefore dx=\sqrt{2}du$ $=\int{\frac{\sqrt{2}du}{\sqrt{2{{u}^{2}}+2}}}$ $=\log (\sqrt{{{u}^{2}}+1}+u$ Undo substitution: $u=\frac{x+1}{\sqrt{2}}$ $\therefore...
$=\int{_{3}^{4}\frac{dx}{4(x-4)}=\int{_{3}^{4}\frac{1}{4(x+2)}dx}}$ $=\frac{1}{4}\log (x-2)-\frac{1}{4}\log (x+2)$ $=\frac{1}{4}\log 3-\frac{1}{4}\log 1-\frac{1}{4}\log 6+\frac{1}{4}\log 5$...
$=\frac{3}{2}\log x-\log (x+2)$ $=\frac{1}{2}(\log 2+\log 3)$
$\int{_{1}^{2}\frac{1}{(x+1)}dx=\int{_{1}^{2}\frac{1}{(x+2)}dx}}$ $=[\log (x+1)-\log (x+2)]_{1}^{2}$ $=2\log 3-3\log 2$
$=\int{_{0}^{2}}\frac{{{x}^{4}}+1}{{{x}^{2}}+1}dx=\int{_{0}^{2}\frac{2}{{{x}^{2}}+1}dx}$ $=\int{_{0}^{2}}\frac{({{x}^{2}}-1)({{x}^{2}}+1)}{{{x}^{2}}+1}dx+\int{_{0}^{2}\frac{2}{{{x}^{2}}+1}dx}$...
$={{2}^{\frac{3}{2}}}\left( \sin \left( \frac{\pi }{4} \right)-0 \right)$ $=\frac{2\sqrt{2}}{\sqrt{2}}$ $=2$
$={{2}^{\frac{2}{5}}}\left( 0-\sin \left( -\frac{\pi }{4} \right) \right)$ $=\frac{2\sqrt{2}}{\sqrt{2}}$ $=2$
$=\frac{1}{2}\left[ \frac{-\cos 5x}{5}+\cos x \right]$ $=\frac{1}{2}\left[ -\frac{\cos (5\pi )}{5}+\cos (\pi ) \right]-\frac{1}{2}\left[ -\frac{\cos (0)}{5}+\cos (0) \right]$ $=\frac{1}{2}\left[...
$=\frac{1}{2}\left[ \frac{\sin 3x}{3}+\sin x \right]$ $=\frac{1}{2}\left[ \frac{\sin \left( \frac{\pi }{3} \right)}{3}+\sin \left( \frac{\pi }{6} \right) \right]-0$ $=\frac{1}{2}\left[...
. 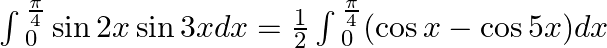
$=\frac{1}{2}\int{_{0}^{\frac{\pi }{4}}(cox-\cos 5x)dx}$ $=\frac{1}{2}\left[ \sin x-\frac{\sin 5x}{5} \right]$ $=\frac{1}{2}\left[ \sin \left( \frac{\pi }{4} \right)-\frac{\sin \left( \frac{5\pi...
$\int{_{\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{dx}{2{{\sin }^{2}}x}=\int{_{\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{1}{2}\frac{dx}{2}\cos e{{c}^{2}}xdx}}$ $\int{_{\frac{\pi }{2}}^{\frac{\pi...
$\int{_{0}^{\frac{\pi }{4}}\frac{dx}{1+\cos 2x}=\int{_{0}^{\frac{\pi }{4}}\frac{1}{2}{{\sec }^{2}}xdx}}$ $\int{_{0}^{\frac{\pi }{4}}\frac{1}{2}{{\sec }^{2}}xdx=\frac{1}{2}[\tan x]}$...
Let $u=\left( \tan \left( \frac{x}{2} \right)+1 \right)$ $dx=\frac{2}{{{\sec }^{2}}\left( \frac{x}{2} \right)}du$ $=-\frac{2}{u}$ $=-\frac{2}{\tan \left( \frac{x}{2} \right)+1}$ $=2$
$\int{_{0}^{\frac{\pi }{4}}(\cos x-\sin x)dx}$ $=[\sin x+\cos x]$ $=\left[ \cos \left( \frac{\pi }{4} \right)+\sin \left( \frac{\pi }{4} \right)-\cos 0-\sin 0 \right]$ $=\left[...
. 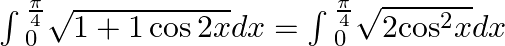
$=\sqrt{2}\left| \sin x \right|$ $\sqrt{2}\left| \sin \left( \frac{\pi }{4} \right)-\sin 0 \right|$ $\sqrt{2}\left[ \frac{1}{\sqrt{2}} \right]$ $=1$
$=\int{_{\frac{\pi }{4}}^{\frac{\pi }{4}}(\cos e{{c}^{2}}(x)-3\cos ec(x)\cot (x)dx}$
$\frac{1}{4}\int{_{0}^{\frac{\pi }{2}}(3\sin x-\sin 3x)dx=\frac{1}{4}\left[ -3\cos x+\frac{\cos 3x}{3} \right]}$ $=\frac{1}{4}\left[ -3\cos \left( \frac{\pi }{2} \right)+\frac{\cos \left( \frac{3\pi...
$\frac{1}{4}\int{_{0}^{\frac{\pi }{3}}(3\cos x-\cos 3x)dx=\frac{1}{4}\left[ 3\sin x+\frac{\sin 3x}{3} \right]}$ $\frac{1}{4}\left[ 3\sin \left( \frac{\pi }{3} \right)+\frac{\sin \pi }{3}...
$=-\log \left| \cos ec\left( \frac{\pi }{4} \right)+\cot \left( \frac{\pi }{4} \right) \right|+\log \left| \cos ec\left( \frac{\pi }{6} \right)+\cot \left( \frac{\pi }{6} \right) \right|$ $=-\log...
$=\log \left| \sec \left( \frac{\pi }{3} \right) \right|-in\left| \cos 0 \right|$ $=\log \left| 2 \right|-\log \left| 1 \right|$ $=\log 2$
$\int{_{0}^{\frac{\pi }{4}}({{\sec }^{2}}x-1)dx=\int{_{0}^{\frac{\pi }{4}}\left[ \tan x-x \right]}}$ $\left[ \tan \left( \frac{\pi }{4} \right)-\frac{\pi }{4}-\tan (0)-0 \right]=\left[ 1-\frac{\pi...
$\int{_{\frac{\pi }{4}}^{\frac{\pi }{2}}(\cos e{{c}^{2}}x-1)dx=[-\cot x-x]}$ $$$=\left[ -\cot \left( \frac{\pi }{2} \right)-\frac{\pi }{2}+\cot \left( \frac{\pi }{4} \right)+\frac{\pi }{4} \right]$...
$=[\tan \left( \frac{\pi }{6} \right)-\tan 0]$ $=\frac{1}{\sqrt{3}}$ Q.14 $\int{_{\frac{-\pi }{4}}^{\frac{\pi }{4}}\cos e{{c}^{2}}xdx=[-\cot x]}$ $\left[ -\cot \left( \frac{\pi }{4} \right)+\cot...
$=[{{\sin }^{-1}}1-{{\sin }^{-1}}0]$ $=\frac{\pi }{2}$
$=[{{\tan }^{-1}}\infty {{\tan }^{-1}}0]$ $=\pi /2$
$=[{{\tan }^{-1}}1-{{\tan }^{-1}}0]$ $=\pi /4$
$=3\left[ 4-2 \right]$ $=6$
$=\left[ 3{{(8)}^{\frac{1}{3}}}-3{{(1)}^{\frac{1}{3}}} \right]$ $=\left[ 6-3 \right]$ $=3$
$=\left[ \frac{3}{2}{{1}^{\frac{4}{3}}}-0 \right]$ $=\frac{3}{2}$
$=\left[ 2\sqrt{4-2} \right]$ $=\left[ 4-2 \right]$ $=2$
$=\left[ \log (-1)-\log (-4) \right]$ $=-\left[ \log (-4)-\log (-1) \right]$ $-\left[ \log \left( \frac{-4}{-1} \right) \right]$ $=-\log 4$
$=\frac{4}{7}\left[ {{16}^{\frac{7}{4}}}-1 \right]$ $=\frac{512}{7}$
$\frac{{{2}^{-4}}}{-4}-\frac{1}{-4}$ $\frac{16-1}{64}$ $\frac{15}{64}$
$\frac{2}{3}\left[ {{4}^{\frac{3}{2}}}-1 \right]$ $=\frac{14}{3}$
$=\frac{{{3}^{5}}}{5}-\frac{1}{5}$ $\frac{243-1}{5}$ $=\frac{243}{5}$

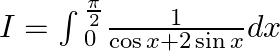
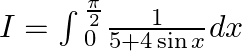
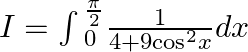
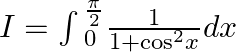
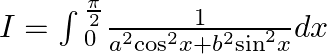
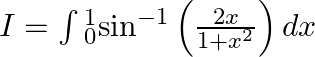
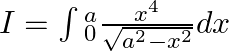
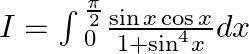
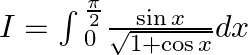
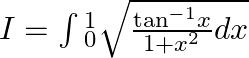
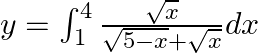
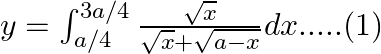
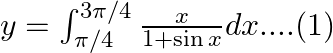
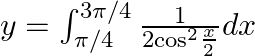
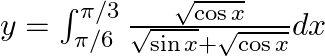
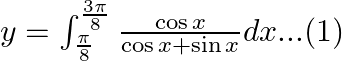
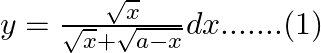
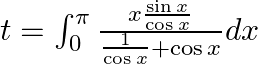
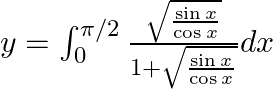
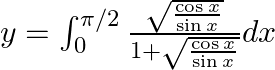
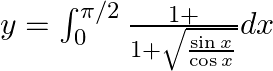
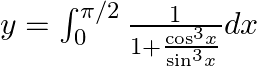
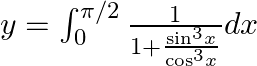
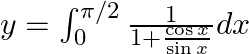
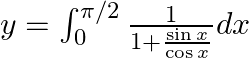
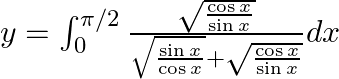
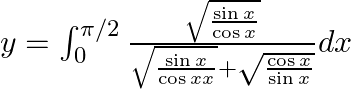
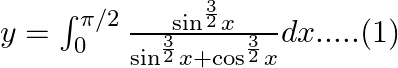
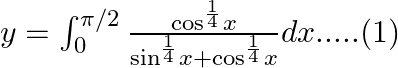
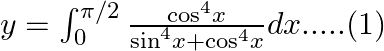
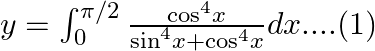
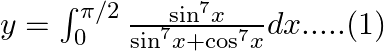
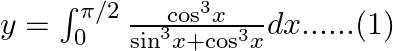
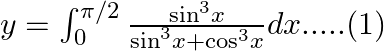
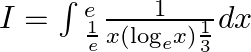
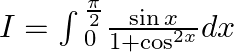
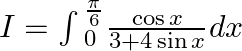
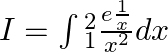
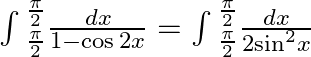
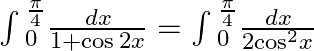
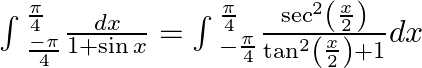
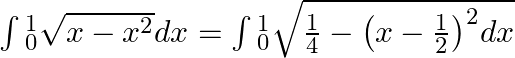
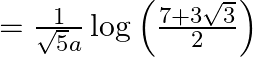
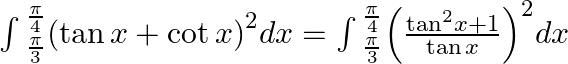
![Rendered by QuickLaTeX.com =\left[ \frac{\pi }{2}\sin \left( \frac{\pi }{4} \right)+\left( 2-\frac{{{\pi }^{2}}}{16} \right)\cos \right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-49ff80c8976376587a9aa088704f8920_l3.png)
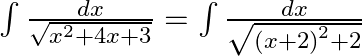
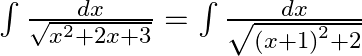
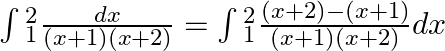
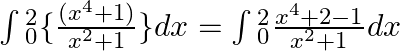
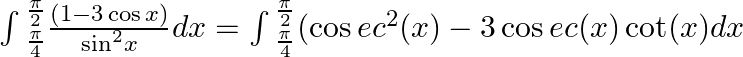
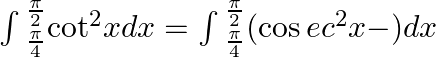
![Rendered by QuickLaTeX.com \int{_{1}^{8}\frac{dx}{{{x}^{\frac{2}{3}}}}=\left[ \frac{3}{1}{{x}^{\frac{1}{3}}} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b8c5ab15ed9d7685ee3cbd659940b0c4_l3.png)
![Rendered by QuickLaTeX.com \int{_{0}^{1}\frac{dx}{3\sqrt{x}}=\left[ \frac{3}{2}{{x}^{\frac{2}{3}}} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-598d81995b16225fcb959e76f1227802_l3.png)
![Rendered by QuickLaTeX.com \int{_{0}^{16}{{x}^{\frac{3}{4}}}dx=\left[ \frac{4}{7}{{x}^{\frac{7}{4}}} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a5289eb5bb96809ad1fc7747e6a02654_l3.png)
![Rendered by QuickLaTeX.com \int{_{1}^{2}{{x}^{-5}}dx=\left[ \frac{{{x}^{-4}}}{-4} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b793472d6e2b499501665d78886a1d89_l3.png)
![Rendered by QuickLaTeX.com \int{_{1}^{4}\sqrt{x}dx=\left[ \frac{2}{3}{{x}^{\frac{3}{2}}} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7f4a1195fbd44abd6c01848b17dba0d5_l3.png)
![Rendered by QuickLaTeX.com \int{_{1}^{3}{{x}^{4}}dx=\left[ \frac{{{x}^{5}}}{5} \right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-062aa044351dc600fbdc6e340df27499_l3.png)