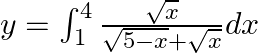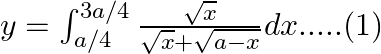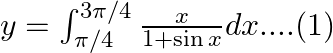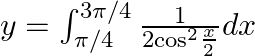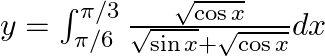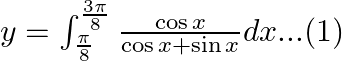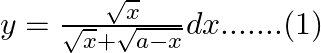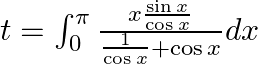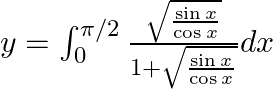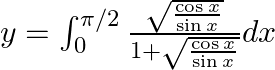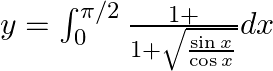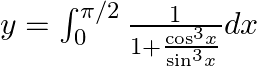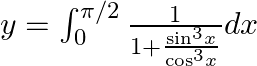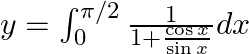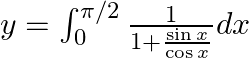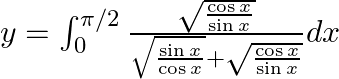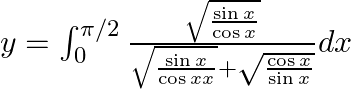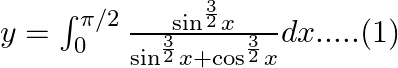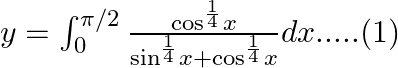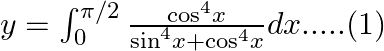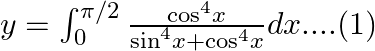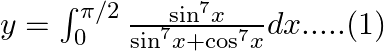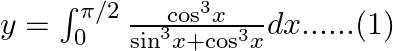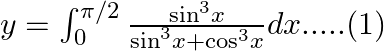$f(x)$is continuous in $\left[ 1,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=1/n$ $\int...

$y=\int _{0}^{4}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx$ $y=\int _{0}^{2}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx+\int _{2}^{4}\left| x \right|+\left| x-2...

$y=\int _{0}^{4}f(x)dx$ $y=\int _{0}^{2}f(x)dx+\int _{2}^{4}f(x)dx$ $y=\int _{0}^{2}3{{x}^{2}}+4dx+\int _{2}^{4}9x-2dx$ $y=\left( {{x}^{3}}+4x \right)_{0}^{2}+\left( \frac{9{{x}^{2}}}{2}-2x...

$y=\int _{1}^{3}f(x)dx$ $y=\int _{1}^{2}f(x)dx+\int _{2}^{3}f(x)dx$ $y=\int _{1}^{2}2x+1dx+\int _{2}^{3}{{x}^{2}}+1dx$ $y=\left( {{x}^{2}}+x \right)_{1}^{2}+\left( \frac{{{x}^{3}}}{3}+x...

We know that $\left| \sin x \right|=-\sin x$in $\left[ -\pi /4,0 \right)$ $\left| \sin x \right|=\sin x$in $\left[ 0,\pi /4 \right]$ $y=\int _{-\pi /4}^{0}\left| \sin x \right|dx+\int _{0}^{\pi...

We know that $\left| \cos x \right|=\cos x$in $\left[ 0,\pi /2 \right)$ $\left| \cos x \right|=-\cos x$in $\left[ \pi /2,3\pi /2 \right)$ $\left| \cos x \right|=\cos x$in $\left[ 3\pi /2,2\pi ...

We know that $\left| x-5 \right|=-(x-5)$in $\left[ 0,5 \right)$ $\left| x-5 \right|=(x-5)$in $\left[ 5,8 \right]$ $y=\int _{0}^{5}\left| x-5 \right|dx+\int _{5}^{8}\left| x-5 \right|dx$ $y=\int...

We know that $\left| x+1 \right|=-(x+1)$in $\left[ -2,-1 \right)$ $\left| x+1 \right|=(x+1)$in $\left[ -1,2 \right]$ $y=\int _{-2}^{-1}\left| x+1 \right|dx+\int _{-1}^{2}\left| x+1 \right|dx$...

We know that $\left| x \right|=-x$in $\left[ -1,0 \right)$ $\left| x \right|=x$in $\left[ 0,1 \right]$ $y=\int _{-1}^{0}{{e}^{\left| x \right|}}dx+\int _{0}^{1}{{e}^{\left| x \right|}}dx$ $y=\int...

$y=\int _{-\pi }^{\pi }{{x}^{12}}{{\sin }^{9}}xdx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\left( \pi -\pi -x...

$y=\int _{-\pi }^{\pi }{{\sin }^{75}}x+{{x}^{125}}dx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\sin }^{75}}\left( \pi -\pi...

$y=\int _{-a}^{a}{{x}^{3}}\sqrt{{{a}^{2}}-{{x}^{2}}dx}.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int...

Let $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ At $x=0,t=0$ At $x=1,t=\pi /4$ \[y=\int _{0}^{\pi /4}\frac{\log \left( 1+\tan t \right)}{1+{{\tan }^{2}}t}{{\sec }^{2}}tdt\] \[y=\int _{0}^{\pi...

Use integration by parts $\int I\times IIdt=I\int IIdt-\int \frac{d}{dt}I\left( \int IIdt \right)dt$ $y=\log x\int \frac{\sqrt{1}}{\sqrt{1-{{x}^{2}}}}dx-\int \frac{d}{dx}\log x\left( \int...

Let, $x=\sin t$ $\Rightarrow dx=\cos tdt$ At $x=0,t=0$ At $x=1,t=\pi /2$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{-1}}\sin t}{\sin t}\cos tdt$ $y=\int _{0}^{\pi /2}\frac{t\cos t}{\sin t}dt$ $y=\int...

Use integration by parts $\int I\times IIdx=I\int IIdx-\int \frac{d}{dx}I\left( \int IIdx \right)dx$ $y=x\int \cot xdx-\int \frac{d}{dx}x\left( \int \cot xdx \right)dx$ $y=\left( x\log \sin x...

Use king theorem of definite integral $\int _{a}^{b}f(x)=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{1}^{4}\frac{\sqrt{4+1-x}}{\sqrt{4+1-x}+\sqrt{x}}dx$ $y=\int...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{a/4}^{3a/4}\frac{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}}{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}+\sqrt{x}}dx$...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /4}^{3\pi /4}\frac{\left( \frac{3\pi }{4}+\frac{\pi }{4}-x \right)}{1+\sin \left( \frac{3\pi...

$y=\frac{1}{2}\int _{\pi /4}^{3\pi /4}{{\sec }^{2}}\frac{x}{2}dx$ $y=\frac{1}{2}\left( \frac{\frac{\tan x}{2}}{\frac{1}{2}} \right)_{\pi /4}^{3\pi /4}$ $y=\tan \frac{3\pi }{8}-\tan \frac{\pi }{8}$...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /6}^{\pi /3}\frac{\sqrt{\cos \left( \frac{\pi }{3}+\frac{\pi }{6}-x \right)}}{\left( \sqrt{\sin...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /8}^{3\pi /8}\frac{\cos \left( \frac{3\pi }{8}+\frac{\pi }{8}-x \right)}{\sin \left( \frac{3\pi...

\[y=\int _{0}^{\pi /2}\log \frac{1}{\sin x\cos x}dx\] \[y=-\left( \int _{0}^{\pi /2}\log \sin xdx+\int _{0}^{\pi /2}\log \cos xdx \right)\] Let, $I=\int _{0}^{\pi /2}\log \sin xdx......(1)$ Use king...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\left( \pi -x \right)\log \sin \left( \pi -x \right)dx$ $y=\int _{0}^{\pi }\pi \log \sin...

$y=\int _{0}^{\pi /2}\log 2+\log \sin x+\log \cos xdx$ Let, $I=\int _{0}^{\pi /2}\log \sin xdx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)$ $I=\int...

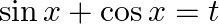
$\Rightarrow \cos x-\sin xdx=dt$ At $x=0,t=1$ At $x=\pi /2,t=1$ $y=\int _{1}^{1}-\log tdt$ We know that when upper and lower limit in definite integral is equal then value of integration is zero....

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }{{\sin }^{2m}}\left( \pi -x \right){{\cos }^{2m+1}}\left( \pi -x \right)dx$ $y=-\int _{0}^{\pi...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }{{\sin }^{2}}\left( \pi -x \right){{\cos }^{3}}\left( \pi -x \right)dx$ $y=-\int _{0}^{\pi...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{a}\frac{\sqrt{a-x}}{\sqrt{a-x}+\sqrt{x}}dx.......(2)$ Adding equation (1) and (2) $2y=\int...

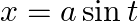
$\Rightarrow dx=a\cos tdt$ At $x=0,t=0$ At $x=a,t=0$ $y=\int _{0}^{\pi /2}\frac{a\cos t}{a\sin t+\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}t}}dt$ $y=\int _{0}^{\pi /2}\frac{\cos t}{\sin t+\cos t}dt$...

$y=\int _{0}^{\pi /2}\log \frac{{{\cos }^{2}}x}{2\sin x\cos x}dx$ $y=\int _{0}^{\pi /2}\log \left( \frac{1}{2}\cot x \right)dx.....(1)$ Use king theorem of definite integral $\int...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)}{1+{{\sin }^{2}}\left( \pi -x \right)}dx$ $y=\int _{0}^{\pi...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\sin \left( \pi -x \right)}{1+\sin \left( \pi -x \right)}dx$ $y=\int...

$y=\int _{0}^{\pi }\frac{x\sin x}{1+{{\cos }^{2}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\sin...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{2}}\left( \frac{\pi }{2}-x \right)}{\sin \left( \frac{\pi }{2}-x \right)+\cos...

Use king theorem of definite  integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi }\frac{\left( \pi -x \right)\tan \left( \pi -x \right)}{\sec \left( \pi -x \right)\cos ec\left(...

$\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{2}(2-x)\sqrt{x}dx$ $y=\int _{0}^{2}2{{x}^{\frac{1}{2}}}-{{x}^{\frac{1}{2}}}dx$ $y=\left(...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{1}(1-x){{x}^{5}}dx$ $y=\int _{0}^{1}{{x}^{5}}-{{x}^{6}}dx$ $y=\left(...

$y=\int _{0}^{\pi /2}\frac{\sqrt{\sin x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ \[y=\int...

$y=\int _{0}^{\pi /2}\frac{\sqrt{\cos x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...

Q15. $y=\int _{0}^{\pi /2}\frac{1+}{1+\sqrt{\frac{\sin x}{\cos x}}}dx$ $y=\int _{0}^{\pi /2}\frac{\sqrt{\cos x}}{\left( \sqrt{\sin x}+\sqrt{\cos x} \right)}dx.....(1)$ Use king theorem of definite...

$y=\int _{0}^{\pi /2}\frac{{{\sin }^{3}}x}{{{\sin }^{3}}x+{{\cos }^{3}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...

$y=\int _{0}^{\pi /2}\frac{{{\cos }^{3}}x}{{{\sin }^{3}}x+{{\cos }^{3}}x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi...

$y=\int _{0}^{\pi /2}\frac{\sin x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ \[y=\int _{0}^{\pi /2}\frac{\sin \left( \frac{\pi...

$y=\int _{0}^{\pi /2}\frac{\cos x}{\sin x+\cos x}dx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\cos \left( \frac{\pi...

$y=\int _{0}^{\pi /2}\frac{\cos x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\cos \left( \frac{\pi...

$y=\int _{0}^{\pi /2}\frac{\sin x}{\sin x+\cos x}dx....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\sin \left( \frac{\pi...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{n}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{n}}\left( \frac{\pi }{2}-x...

Use king theorem of definite integral \[\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx\] \[y=\int _{0}^{\pi /2}\frac{{{\sin }^{\frac{3}{2}}}\left( \frac{\pi }{2}-x \right)}{{{\sin...

Use king theorem definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{\frac{1}{4}}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{\frac{1}{4}}}\left(...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{4}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{4}}\left( \frac{\pi }{2}-x...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{4}}\left( \frac{\pi }{4}-x \right)}{{{\sin }^{4}}\left( \frac{\pi }{2}...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{7}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{7}}\left( \frac{\pi }{2}-x...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{{{\cos }^{3}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{3}}\left( \frac{\pi }{2}-x...

Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{b}^{\pi /2}\frac{{{\sin }^{3}}\left( \frac{\pi }{2}-x \right)}{{{\sin }^{3}}\left( \frac{\pi }{2}-x...

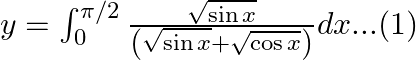
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{0}^{\pi /2}\frac{\sqrt{\sin \left( \frac{\pi }{2}-x \right)}}{\left( \sqrt{\sin \left( \frac{\pi }{2}-x...

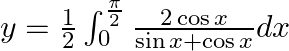
$=\frac{1}{2}\int _{0}^{\frac{\pi }{2}}\frac{\cos x+\cos x-\sin x+\sin x}{\sin x+\cos x}dx$ $=\frac{1}{2}\int _{0}^{\frac{\pi }{2}}1+\frac{\cos x-\sin x}{\sin x+\cos x}dx$ $=\frac{1}{2}\left( \left(...