Solution: The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element $a_{j i}$ shifted to new position $a_{j i}$. The symmetric matrix is defined...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}2 & 3 \\ 1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7da3aec34a65e6e0aeb82a3f6a232300_l3.png) and
and 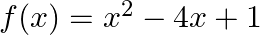 , find
, find 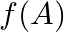 .
.
Solution: We have $A=\left(\begin{array}{ll}2 & 3 \\ 1 & 2\end{array}\right)$. Now addition/subtraction of two matrices is possible if order of both the matrices are same and multiplication...
If A and B are symmetric matrices of the same order, show that (AB – BA) is a skew symmetric matrix.
Solution: We have $A$ and $B$ are symmetric matrices. Therefore $A^{T}=A$ and $B^{T}=B$ The transpose of the matrix is an operation of making interchange of elements by the rule on positioned...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b5c8c8d44a123b24c17830efc625a77b_l3.png) , show that
, show that  .
.
Solution: We have $A=\left(\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right)$. The transpose of the matrix is an operation of making interchange of...
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}4 & 2 \\ 1 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd81dbbffa9684064602a99b2f36c226_l3.png) and
and ![Rendered by QuickLaTeX.com \mathrm{B}=\left[\begin{array}{cc}-2 & 1 \\ 3 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aefeccc89d0278dab4e14dc06c63bae5_l3.png) , find a matrix
, find a matrix 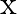 such that
such that 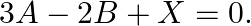
Solution: We have $A=\left(\begin{array}{ll}4 & 2 \\ 1 & 3\end{array}\right), B=\left(\begin{array}{cc}-2 & 1 \\ 3 & 2\end{array}\right)$ and $3 A-2 B+X=0$ We can have the addition...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}2 & -3 \\ 4 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-40f9b0b32323b8d7e2a6115865036362_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}-1 & 2 \\ 0 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2386be89f405fcc8381ad1375da5f2f9_l3.png) , find a matrix
, find a matrix  such that
such that 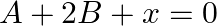 .
.
Solution: We have $A=\left(\begin{array}{cc}2 & -3 \\ 4 & 5\end{array}\right), B=\left(\begin{array}{cc}-1 & 2 \\ 0 & 3\end{array}\right)$ and $A+2 B+X=0$. We can have the addition...
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}2 & 3 \\ 4 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-78ffcac901c4b797c4a133f9d5e818a9_l3.png) , and show that
, and show that 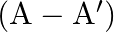 is skew-symmetric
is skew-symmetric
Solution: We have $\left(\begin{array}{ll}2 & 3 \\ 4 & 5\end{array}\right)$. The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element...
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}4 & 5 \\ 1 & 8\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8158b32a662df332e0a5eb4fe7a2edb9_l3.png) , show that
, show that 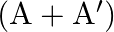 is symmetric
is symmetric
Solution: We have $\left(\begin{array}{ll}4 & 5 \\ 1 & 8\end{array}\right)$. The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element...
Find the value of  and
and  for which
for which ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} \mathrm{x} & \mathrm{y} \\ 3 \mathrm{y} & \mathrm{x} \end{array}\right]\left[\begin{array}{l} 1 \\ 2 \end{array}\right]=\left[\begin{array}{l} 3 \\ 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0863b7d782cc25f6aa50594877777cc3_l3.png)
Solution: We have $\left(\begin{array}{cc}x & y \\ 3 y & x\end{array}\right)\left(\begin{array}{l}1 \\ 2\end{array}\right)=\left(\begin{array}{l}3 \\ 5\end{array}\right)$. Use the...
Find the value of  and
and  for which
for which ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 2 & -3 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \end{array}\right]=\left[\begin{array}{l} 1 \\ 3 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4bea77a5649bdf186a1bac7467012af0_l3.png)
Solution: We have $\left(\begin{array}{cc}2 & -3 \\ 1 & 1\end{array}\right)\left(\begin{array}{l}x \\ y\end{array}\right)=\left(\begin{array}{l}1 \\ 3\end{array}\right)$. Use the...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-237a953de1ebc9d655318073b827c503_l3.png) then find the least value of
then find the least value of 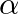 for which
for which 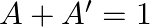 .
.
Solution: We have $A=\left(\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{array}\right)$ Use the addition rule and get $A+A^{T}=I_{2}$ as follow:...
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{cr}1 & -5 \\ -3 & 2 \\ 4 & -2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b75e51d5c2d1c5e218878039b0ef52a7_l3.png) and
and ![Rendered by QuickLaTeX.com \mathrm{B}=\left[\begin{array}{cc}3 & 1 \\ 2 & -1 \\ -2 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4438109c3e36aa09efaebe02d6551a19_l3.png) , find the matrix
, find the matrix 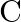 such that
such that 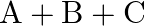 is a zero matrix
is a zero matrix
Solution: We have $A=\left(\begin{array}{cc}1 & -5 \\ -3 & 2 \\ 4 & -2\end{array}\right) ; B=\left(\begin{array}{cc}3 & 1 \\ 2 & -1 \\ -2 & 3\end{array}\right) .$ and...
Show that
![Rendered by QuickLaTeX.com \begin{array}{l} \cos \theta \cdot\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]+\sin \theta \\ {\left[\begin{array}{cc} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{array}\right]=I} \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9f6e84acdf2d6d135e00de04b3a005f2_l3.png)
Solution: We have $\cos \theta\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right)+\sin \theta\left(\begin{array}{cc}\sin \theta & -\cos...
If A = diag (3 -2, 5) and B = diag (1 3 -4), find (A + B).
Solution: We have $A=\operatorname{diag}(3-25)=\left(\begin{array}{ccc}3 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 5\end{array}\right) ; B=$...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}x & 6 \\ -1 & 2 w\end{array}\right]+\left[\begin{array}{cc}4 & x+y \\ z+w & 3\end{array}\right]=3\left[\begin{array}{cc}x & y \\ z & w\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3458f4e6f17d7e715a86e43d08489614_l3.png) , find the values of
, find the values of 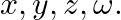
Solution: We have $\left(\begin{array}{cc}x & 6 \\ -1 & 2 w\end{array}\right)+\left(\begin{array}{cc}4 & x+y \\ z+w & 3\end{array}\right)=3\left(\begin{array}{cc}x & y \\ z &...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}x & 3 x-y \\ 2 x+z & 3 y-w\end{array}\right]=\left[\begin{array}{ll}3 & 2 \\ 4 & 7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-611c97c74d8c38eb224393d8f387948c_l3.png) , find the values of
, find the values of 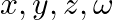 .
.
Solution: We have $\left(\begin{array}{cc}x & 3 x-y \\ 2 x+z & 3 y-w\end{array}\right)=\left(\begin{array}{ll}3 & 2 \\ 4 & 7\end{array}\right)$. Now from the equality of matrices we...
If ![Rendered by QuickLaTeX.com x \cdot\left[\begin{array}{l}2 \\ 3\end{array}\right]+y \cdot\left[\begin{array}{c}-1 \\ 1\end{array}\right]=\left[\begin{array}{r}10 \\ 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b06993b29db939642e38c580586c51db_l3.png) , find the values of
, find the values of  and
and  .
.
Solution: We have $x\left(\begin{array}{l}2 \\ 3\end{array}\right)+y\left(\begin{array}{c}-1 \\ 1\end{array}\right)=\left(\begin{array}{c}10 \\ 5\end{array}\right)$. Use the addition rule and get...
Find the values of  and
and  , if
, if ![Rendered by QuickLaTeX.com 2\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]+\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]=\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e3b199653bed94af618cb5f0d4f0ec35_l3.png)
Solution: We have $2\left(\begin{array}{ll}1 & 3 \\ 0 & x\end{array}\right)+\left(\begin{array}{ll}y & 0 \\ 1 & 2\end{array}\right)=\left(\begin{array}{ll}5 & 6 \\ 1 &...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}x+2 y & -y \\ 3 x & 4\end{array}\right]=\left[\begin{array}{cc}-4 & 3 \\ 6 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-33d06ec59a67edd192829f442472121d_l3.png) , find the values of
, find the values of  and
and 
Solution: We have $\left(\begin{array}{cc}x+2 y & -y \\ 3 x & 4\end{array}\right)=\left(\begin{array}{cc}-4 & 3 \\ 6 & 4\end{array}\right)$ Now from the equality of matrices we can...
Construct a  matrix whose elements are given by
matrix whose elements are given by 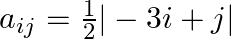
Solution: We have $a_{i j}=\frac{1}{2}|-3 i+j|^{2}$ Now $\begin{array}{l} a_{11}=\frac{|-3(1)+1|}{2}=1, a_{12}=\frac{|-3(1)+2|}{2}=\frac{9}{2}, a_{13}=\frac{|-3(1)+3|}{2}=\frac{9}{2} \\...
Construct a  matrix whose elements are given by
matrix whose elements are given by 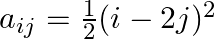
Solution: We have $a_{i j}=\frac{1}{2}(i-2 j)^{2}$ Now $\begin{array}{l} a_{11}=\frac{(1-2(1))^{2}}{2}=\frac{1}{2}, a_{12}=\frac{(1-2(2))^{2}}{2}=\frac{9}{2} \\ a_{21}=\frac{(2-2(1))^{2}}{2}=0...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f03cb7f5858669bd60950918832693a7_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}-1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 3 & 0 & -1 \\ 2 & 3 & 0 \\ 0 & 4 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-25dedef54c4e0355d69496a2dc00aa7b_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}1 & 2 & 3 \\ 2 & 5 & 7 \\ -2 & -4 & -5\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 5 & 7 \\ -2 & -4 & -5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9b986c3bb2233699ef7411fc62105e4b_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}1 & 2 & 3 \\ 2 & 5 & 7 \\ -2 & -4 & -5\end{array}\right)$. To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 1 & 3 & -2 \\ -3 & 0 & -1 \\ 2 & 1 & 0 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a91ce5cbcf073815176a56b34ba47bd9_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}1 & 3 & -2 \\ -3 & 0 & -1 \\ 2 & 1 & 0\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 3 & -1 & -2 \\ 2 & 0 & -1 \\ 3 & -5 & 0 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6f98ac5a8bdc0a4c68b59ad5fff13f27_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}3 & -1 & -2 \\ 2 & 0 & -1 \\ 3 & -5 & 0\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 1 & 2 & -3 \\ 2 & 3 & 2 \\ 3 & -3 & -4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a3c18e3e41c6018e29633c0543144480_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}1 & 2 & -3 \\ 2 & 3 & 2 \\ 3 & -3 & -4\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{lll} 3 & 0 & 2 \\ 1 & 5 & 9 \\ 6 & 4 & 7 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c2d4be16f7e50993b9d9ddb636e32da5_l3.png)
Solution: We have $A=\left(\begin{array}{lll}3 & 0 & 2 \\ 1 & 5 & 9 \\ 6 & 4 & 7\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-17264154c86fb2057da2439f6e8db1ee_l3.png)
Solution: We have $A=\left(\begin{array}{ccc}2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9e97cd7932741e795ff74dfcc62f2080_l3.png)
Solution: We have $A=\left(\begin{array}{lll}0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 6 & 7 \\ 8 & 9 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-720c2b2a18ed5a12137848fe6835b85c_l3.png)
Solution: We have $A=\left(\begin{array}{ll}6 & 7 \\ 8 & 9\end{array}\right)$. To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 4 & 0 \\ 2 & 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-00e067d8b3d687152537a9d78c193c7f_l3.png)
Solution: We have $A=\left(\begin{array}{ll}4 & 0 \\ 2 & 5\end{array}\right)$. To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 2 & -3 \\ 4 & 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6d086db9247d6fa2dd93801088be8f5f_l3.png)
Solution: We have $A=\left(\begin{array}{cc}2 & -3 \\ 4 & 5\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{rr} 2 & 5 \\ -3 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4e7a3750c7e99f5875f5fe5e581bc3bc_l3.png)
Solution: We have $A=\left(\begin{array}{cc}2 & 5 \\ -3 & 1\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 1 & 2 \\ 2 & -1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-918a8e2a33fbf14a8141e6d365aa3df9_l3.png)
Solution: We have $A=\left(\begin{array}{cc}1 & 2 \\ 2 & -1\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 1 & 2 \\ 3 & 7 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6a1968e1a662e8c4373a2fec80dd99d1_l3.png)
Solution: We have $A=\left(\begin{array}{ll}1 & 2 \\ 3 & 7\end{array}\right)$ To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
If matrix ![Rendered by QuickLaTeX.com A=[123]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-10126ffe9d6b60c09e88f578316796d6_l3.png) , write
, write 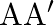 .
.
Solution: Given that $A=\left[\begin{array}{ll}1 & 23\end{array}\right]$ We will find $A$ ' to calculate AA': $\mathrm{A}^{\prime}=\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]$ Now...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b5c8c8d44a123b24c17830efc625a77b_l3.png) , show that
, show that 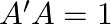 .
.
Solution: Given that $A=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \theta & \cos \alpha\end{array}\right]$. We wil find $A$ $A^{\prime}=\left[\begin{array}{cc}\cos \alpha...
For each of the following pairs of matrices  and
and  , verify that
, verify that 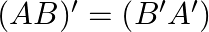 :
: ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}-1 & 2 & -3 \\ 4 & -5 & 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4b8a6371313bb6ec237c7ac8ff4e7f9d_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}3 & -4 \\ 2 & 1 \\ -1 & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d5b55b58779f0457b2c521b7bc825595_l3.png)
Solution: Take $\mathrm{C}=\mathrm{AB}$ $\begin{array}{l} C=\left[\begin{array}{ccc} -1 & 2 & -3 \\ 4 & -5 & 6 \end{array}\right]\left[\begin{array}{cc} 3 & -4 \\ 2 & 1 \\ -1...
For each of the following pairs of matrices  and
and  , verify that
, verify that 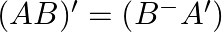 :
: ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{c} -1 \\ 2 \\ 3 \end{array}\right] \text { and } \mathrm{B}=[-2 \cdot 1-4]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-86cfd44f3d05fdc26f7ec6f9a464ad20_l3.png)
Solution: Take $C=A B$ $\begin{array}{l} C=\left[\begin{array}{c} -1 \\ 2 \\ 3 \end{array}\right]\left[\begin{array}{lll} -2 & -1 & -4 \end{array}\right] \\...
For each of the following pairs of matrices  and
and  , verify that
, verify that 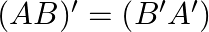 :
: ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr} 3 & -1 \\ 2 & -2 \end{array}\right] \text { and } B=\left[\begin{array}{rr} 1 & -3 \\ 2 & -1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3f4483ea07db74116ba0bc5d55287e5b_l3.png)
Solution: Take $C=A B$ $\begin{array}{l} C=\left[\begin{array}{rr} 3 & -1 \\ 2 & -2 \end{array}\right]\left[\begin{array}{ll} 1 & -3 \\ 2 & -1 \end{array}\right] \\...
For each of the following pairs of matrices  and
and  , verify that
, verify that 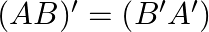 :
: ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll} 1 & 3 \\ 2 & 4 \end{array}\right] \text { and } B=\left[\begin{array}{ll} 1 & 4 \\ 2 & 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c3667d21de9c5134248177485655ffeb_l3.png)
Solution: Take $\mathrm{C}=\mathrm{A} 8$ $\begin{array}{l} C=\left[\begin{array}{ll} 1 & 3 \\ 2 & 4 \end{array}\right]\left[\begin{array}{ll} 1 & 4 \\ 2 & 5 \end{array}\right] \\...
Express the matrix ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll}3 & 2 & 5 \\ 4 & 1 & 3 \\ 0 & 6 & 7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7aaa077b9058e56f42a554ca8fcb171f_l3.png) as sum af two matrices such that and is symmetric and the other is skew-symmetric.
as sum af two matrices such that and is symmetric and the other is skew-symmetric.
Solution: Given that $A=\left[\begin{array}{lll}3 & 2 & 5 \\ 4 & 1 & 3 \\ 0 & 6 & 7\end{array}\right]$, to express as sum of symmetric matrix $P$ and skew symmetric matrix...
Express the matrix A as the sum of a symmetric and a skew-symmetric matrix, where ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}3 & -1 & 0 \\ 2 & 0 & 3 \\ 1 & -1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1b1e9a45433f3d96b64a151e3b79bd27_l3.png) .
.
Solution: Given that $A=\left[\begin{array}{ccc}3 & -1 & 0 \\ 2 & 0 & 3 \\ 1 & -1 & 2\end{array}\right]$, to express as sum of symmetric matrix $P$ and skew symmetric matrix...
Express the matrix ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ccc}-1 & 5 & 1 \\ 2 & 3 & 4 \\ 7 & 0 & 9\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7350e822cb973005882ae131c2364e63_l3.png) as the sum of a symmetric and a skew-symmetric matrix.
as the sum of a symmetric and a skew-symmetric matrix.
Solution: Given that $\mathrm{A}=\left[\begin{array}{ccc}-1 & 5 & 1 \\ 2 & 3 & 4 \\ 7 & 0 & 9\end{array}\right]$, to express as sum of symmetric matrix $\mathrm{P}$ and skew...
Express the matrix ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{rr}3 & -4 \\ 1 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4c224184d619670975e11f1ad1098530_l3.png) as the sum of a symmetric matrix and a skew-symmetric matrix.
as the sum of a symmetric matrix and a skew-symmetric matrix.
Solution: Given that $\mathrm{A}=\left[\begin{array}{rr}3 & -4 \\ 1 & -1\end{array}\right]$,to express as the sum of symmetric matrix $\mathrm{P}$ and skew symmetric matrix Q. $A=P+Q$ Where...
Express the matrix ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{cc}2 & 3 \\ -1 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0327e38dfafec712de874ce9c4347484_l3.png) as the sum of a symmetric matrix and a skew-symmetric matrix.
as the sum of a symmetric matrix and a skew-symmetric matrix.
Solution: Given that $A=\left[\begin{array}{cc}2 & 3 \\ -1 & 4\end{array}\right]$, As for a symmetric matrix $A^{\prime}=A$ hence $\begin{array}{l} A+A^{\prime}=2 A \\...
Show that the matrix ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ccc}0 & \mathrm{a} & \mathrm{b} \\ -\mathrm{a} & 0 & \mathrm{c} \\ -\mathrm{b} & -\mathrm{c} & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-46d4fca5a1e4ccd3daf4e4683a818d9d_l3.png) is skew-symmetric.
is skew-symmetric.
Solution: We have $A=\left(\begin{array}{ccc}0 & a & b \\ -a & 0 & c \\ -b & -c & 0\end{array}\right)$. The transpose of the matrix is an operation of making interchange of...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & -4 \\ 1 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-16f776216ed4662f25a9fa186c592e2f_l3.png) , show that
, show that 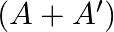 is skew-symmetric.
is skew-symmetric.
Solution: We have $A=\left(\begin{array}{ll}3 & -4 \\ 1 & -1\end{array}\right)$ The transpose of the matrix is an operation of making interchange of elements by the rule on positioned...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}4 & 1 \\ 5 & 8\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd8607c366b843d16c49d92af8d1f55_l3.png) , show that
, show that 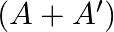 is symmetric.
is symmetric.
Solution: We have $A=\left(\begin{array}{ll}4 & 1 \\ 5 & 8\end{array}\right)$. The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element...
If ![Rendered by QuickLaTeX.com P=\left[\begin{array}{rr}3 & 4 \\ 2 & -1 \\ 0 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-25a68e7dd1de3e3d940408c0f29c6ce9_l3.png) and
and ![Rendered by QuickLaTeX.com P=\left[\begin{array}{cc}7 & -5 \\ -4 & 0 \\ 2 & 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0609e63fb51547a4b3ca4db5d7e945bf_l3.png) , verify that
, verify that 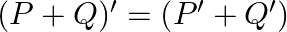
Solution: We have $P=\left(\begin{array}{cc}3 & 4 \\ 2 & -1 \\ 0 & 5\end{array}\right)$ and $Q=\left(\begin{array}{cc}7 & -5 \\ -4 & 0 \\ 2 & 6\end{array}\right)$. The...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}3 & 2 & -1 \\ -5 & 0 & -6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c32e17bbb774b334da0bf3fafe18b27e_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{ccc}-4 & -5 & -2 \\ 3 & 1 & 8\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-733024809307a4305930fcb87f2b032f_l3.png) , verify that
, verify that 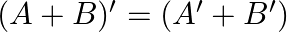 .
.
Solution: We have $A=\left(\begin{array}{ccc}3 & 2 & -1 \\ -5 & 0 & -6\end{array}\right)$ and $B=\left(\begin{array}{ccc}-4 & -5 & -2 \\ 3 & 1 & 8\end{array}\right)$....
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3 & 5 \\ -2 & 0 \\ 4 & -6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1b5da973e1eb1c39298d165a510a5b93_l3.png) , verify that
, verify that 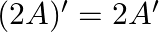 .
.
Solution: We have $A=\left(\begin{array}{cc}3 & 5 \\ -2 & 0 \\ 4 & -6\end{array}\right)$. Thus $2 A=\left(\begin{array}{cc}6 & 10 \\ -4 & 0 \\ 8 & -12\end{array}\right)$ The...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2 & -3 & 5 \\ 0 & 7 & -4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6ac0f76ea62d4473fa0142e884721096_l3.png) , verify that
, verify that 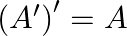 .
.
Solution: We have $A=\left(\begin{array}{ccc}2 & -3 & 5 \\ 0 & 7 & -4\end{array}\right)$. The transpose of the matrix is an operation of making interchange of elements by the rule on...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2 & 3 \\ 5 & 7\end{array}\right]\left[\begin{array}{cc}1 & -3 \\ -2 & 4\end{array}\right]=\left[\begin{array}{cc}-4 & 6 \\ -9 & \mathrm{x}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6910ac8e55e169c0e6b215dd371a238c_l3.png) , find the value of
, find the value of 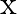
Solution: We have $A=\left(\begin{array}{ll}2 & 3 \\ 5 & 7\end{array}\right), B=\left(\begin{array}{cc}1 & -3 \\ -2 & 4\end{array}\right)$ and $C=\left(\begin{array}{cc}-4 & 6 \\...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}1 & 0 \\ -1 & 7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4b294a697ebb148d82263ae46fb13478_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}0 & 4 \\ -1 & 7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-170fe1f79db53b97fc71e66a945d55c8_l3.png) , find
, find 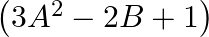 .
.
Solution: We have $A=\left(\begin{array}{cc}1 & 0 \\ -1 & 7\end{array}\right), B=\left(\begin{array}{cc}0 & 4 \\ -1 & 7\end{array}\right)$. (i) Let's compute first $A^{2}$ $A^{2}=A...
Give an example of three matrices A, B, C such that AB = AC but B ≠ C.
Solution: We have $\boldsymbol{A B}=\boldsymbol{A} \boldsymbol{C}$ but $\boldsymbol{B} \neq \boldsymbol{C}$. WE need to find: $\boldsymbol{A}, \boldsymbol{B}$. Let's take...
Given an example of two matrices A and B such that A ≠ O, B ≠ O, AB = O and BA ≠ O.
Solution: We have $\boldsymbol{A} \neq \boldsymbol{O}, \boldsymbol{B} \neq \boldsymbol{O}, \boldsymbol{A B}=\boldsymbol{O}$ and $\boldsymbol{B A} \neq \boldsymbol{O}$. We need to find:...
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b68ab71b95db056eec8874de20c73761_l3.png) , prove that
, prove that ![Rendered by QuickLaTeX.com \mathrm{A}^{\mathrm{n}}=\left[\begin{array}{ll}1 & \mathrm{n} \\ 0 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c75542afc0bd2c36924570507619d8df_l3.png) for all
for all 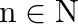 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{1} & \mathbf{1} \\ \mathbf{0} & \mathbf{1}\end{array}\right)$. We need to show: $A^{n}=\left(\begin{array}{ll}1 & n \\ 0...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3 & 4 \\ -4 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fec9588c04898858cde19179ff79aa8f_l3.png) , find
, find 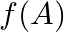 , where
, where 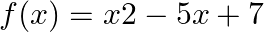 .
.
Solution: We have $A=\left(\begin{array}{cc}3 & 4 \\ -4 & -3\end{array}\right)$ and equation $f(x)=x^{2}-5 x+7$. (i) Let us compute first $A^{2}$ $A^{2}=A A=\left(\begin{array}{cc} 3 & 4...
Find the values of 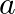 and
and 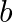 for which
for which ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} a & b \\ -a & 2 b \end{array}\right]\left[\begin{array}{c} 2 \\ -1 \end{array}\right]=\left[\begin{array}{l} 5 \\ 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-54ffd2f53dfe0a81dce111e7e3dda667_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\boldsymbol{a} & \boldsymbol{b} \\ -\boldsymbol{a} & \boldsymbol{2} \boldsymbol{b}\end{array}\right),...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{lll}x & 4 & 1\end{array}\right]\left[\begin{array}{ccc}2 & 1 & 2 \\ 1 & 0 & 2 \\ 0 & 2 & -4\end{array}\right]\left[\begin{array}{c}x \\ 4 \\ -1\end{array}\right]=\mathrm{O}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-95fdea3519bebde2f1b28d9c4f95bf38_l3.png) , find
, find 
Solution: We have $A=\left(\begin{array}{ccc}2 & 1 & 2 \\ 1 & 0 & 2 \\ 0 & 2 & -4\end{array}\right), B=\left(\begin{array}{lll}x & 4 & 1\end{array}\right)$ and...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{lll}1 & x & 1\end{array}\right]\left[\begin{array}{ccc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 5\end{array}\right]\left[\begin{array}{c}1 \\ -2 \\ 3\end{array}\right]=\mathrm{O}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4941f73e6b8cc12c72d34e0f4983af39_l3.png) , find
, find 
Solution: We have $A=\left(\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 5\end{array}\right), B=\left(\begin{array}{lll}1 & x & 1\end{array}\right)$ and...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b5c8c8d44a123b24c17830efc625a77b_l3.png) , show that
, show that ![Rendered by QuickLaTeX.com A^{2}=\left[\begin{array}{cc}\cos 2 \alpha & \sin 2 \alpha \\ -\sin 2 \alpha & \cos 2 \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-004ae2a0cb0effd2df50d6aef24065f4_l3.png)
Solution: We have $A=\left(\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha\end{array}\right)$ and to show $A^{2}=$ $\left(\begin{array}{cc}\cos ^2 \alpha & \sin...
If ![Rendered by QuickLaTeX.com F(x)=\left[\begin{array}{ccc}\cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fe54b977730cd78576884611e79ac060_l3.png) , show that
, show that 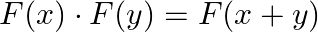
Solution: We have $\boldsymbol{F}(\boldsymbol{X})=\left(\begin{array}{ccc}\cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1\end{array}\right)$ and to show...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}1 & -1 \\ 2 & -1\end{array}\right], B=\left[\begin{array}{rr}a & -1 \\ b & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7966787aabbac62e99a047018387f869_l3.png) and
and 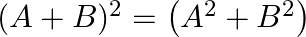 then find the values of
then find the values of 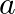 and
and 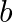 .
.
Solution: We have $A=\left(\begin{array}{ll}1 & -1 \\ 2 & -1\end{array}\right), B=\left(\begin{array}{ll}a & -1 \\ b & -1\end{array}\right)$ and $(A+B)^{2}=\left(A^{2}+\right.$...
Find the matrix A such that A. ![Rendered by QuickLaTeX.com \left[\begin{array}{ll}2 & 3 \\ 4 & 5\end{array}\right]=\left[\begin{array}{cc}0 & -4 \\ 10 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-870749f112d49ec389561d6cc400b796_l3.png) .
.
Solution: We have $\boldsymbol{B}=\left(\begin{array}{ll}\mathbf{2} & \mathbf{3} \\ \mathbf{4} & \mathbf{5}\end{array}\right)$ and $\boldsymbol{C}=\left(\begin{array}{cc}\mathbf{0} &...
Find the matrix A such that ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}5 & -7 \\ -2 & 3\end{array}\right] \cdot \mathrm{A}=\left[\begin{array}{cc}-16 & -6 \\ 7 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-633e2dddcd4fd5ca06e3048dd98f602c_l3.png) .
.
Solution: We have $\boldsymbol{B}=\left(\begin{array}{cc}\mathbf{5} & -\mathbf{7} \\ -\mathbf{2} & \mathbf{3}\end{array}\right)$ and $\boldsymbol{C}=\left(\begin{array}{cc}-\mathbf{1 6}...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & 2 \\ 1 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-866d9f588aa87affb3349473fc083592_l3.png) , find the value of a and
, find the value of a and 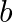 such that
such that 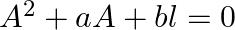
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{3} & \mathbf{2} \\ \mathbf{1} & \mathbf{1}\end{array}\right)$. To find $\boldsymbol{a}, \boldsymbol{b}$ such that...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & 1 \\ 7 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0988384a97f81e0966a9037a51b5ab9b_l3.png) , find
, find  and
and  such that
such that 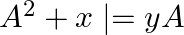 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{3} & \mathbf{1} \\ \mathbf{7} & \mathbf{5}\end{array}\right)$. To find $\boldsymbol{x}, \boldsymbol{y}$ such that...
Solve for  and
and  , when
, when ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 3 & -4 \\ 1 & 2 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \end{array}\right]=\left[\begin{array}{l} 3 \\ 11 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-16dd3658e32c62682e7e1c991959454b_l3.png)
Solution: We have $A=\left(\begin{array}{cc}3 & -4 \\ 1 & 2\end{array}\right), B=\left(\begin{array}{c}3 \\ 11\end{array}\right)$ and $X=\left(\begin{array}{l}x \\ y\end{array}\right)$. We...
Find the values of  and
and  , when
, when ![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 2 & -3 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} \mathrm{x} \\ \mathrm{y} \end{array}\right]=\left[\begin{array}{l} 1 \\ 3 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4bea77a5649bdf186a1bac7467012af0_l3.png)
Solution: We have $A=\left(\begin{array}{cc}2 & -3 \\ 1 & 1\end{array}\right), B=\left(\begin{array}{l}1 \\ 3\end{array}\right)$ and $X=\left(\begin{array}{l}x \\ y\end{array}\right)$. To...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}1 & 2 \\ 4 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8fe923545e5bdad93e0724bc71eca803_l3.png) and
and 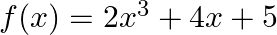 , find
, find 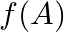 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{1} & \mathbf{2} \\ \mathbf{4} & \mathbf{- 3}\end{array}\right)$. Now addition/subtraction of two matrices is possible if...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}-1 & 2 \\ 3 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-abd4fa7d6a73d83d97ab6e13a9b5a009_l3.png) , find
, find 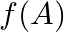 , where
, where 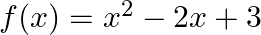
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}-1 & 2 \\ 3 & 1\end{array}\right)$. Now addition/subtraction of two matrices is possible if order of both the matrices are same and...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}3 & -2 \\ 4 & -2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dcf4081f0dd51325845f0b232bbdf385_l3.png) , find
, find  so that
so that 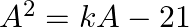 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{3} & -\mathbf{2} \\ \mathbf{4} & -\mathbf{2}\end{array}\right)$. Now addition/subtraction of two matrices is possible if...
Show that the matrix ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}2 & 3 \\ 1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a90c945b5fcc948c6a2940f9dbfc3dcf_l3.png) satisfies the equation
satisfies the equation 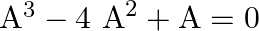 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{2} & \mathbf{3} \\ \mathbf{1} & \mathbf{2}\end{array}\right)$. Now addition of two matrices is possible if order of both the...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3 & 1 \\ -1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ba6b294e8b773dce761b0691a57562ee_l3.png) , show that
, show that 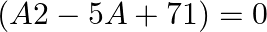 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{3} & \mathbf{1} \\ -\mathbf{1} & \mathbf{2}\end{array}\right)$. Now addition of two matrices is possible if order of both the...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}2 & -2 \\ -3 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-27e32a8a28ce812aeb94edeb354a68bd_l3.png) then find
then find 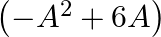
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{2} & \mathbf{- 2} \\ -\mathbf{3} & \mathbf{4}\end{array}\right)$. Now addition of two matrices is possible if order of both...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}2 & -1 \\ 3 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4aecc6df45ed27297ab2d5657e1884ca_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}0 & 4 \\ -1 & 7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-170fe1f79db53b97fc71e66a945d55c8_l3.png) , find
, find 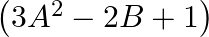 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{2} & \mathbf{- 1} \\ \mathbf{3} & \mathbf{2}\end{array}\right)$ and $\boldsymbol{B}=\left(\begin{array}{cc}\mathbf{0} &...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}4 & -1 & -4 \\ 3 & 0 & -4 \\ 3 & -1 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2d60fb53e459506aacf730b3fd4b58ff_l3.png) , show that
, show that 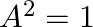
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{4} & -\mathbf{1} & -\mathbf{4} \\ \mathbf{3} & \mathbf{0} & -\mathbf{4} \\ \mathbf{3} & -\mathbf{1} &...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9fe04bd131b7b3438ccdb0c839265f03_l3.png) , show that
, show that 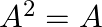
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{2} & \mathbf{- 2} & -\mathbf{4} \\ \mathbf{- 1} & \mathbf{3} & \mathbf{4} \\ \mathbf{1} & -\mathbf{2} &...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}a b & b^{2} \\ -a^{2} & -a b\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-69596ec6bdf3b660c44b6d9df9581f38_l3.png) , show that
, show that 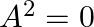 .
.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\boldsymbol{a} \boldsymbol{b} & \boldsymbol{b}^{2} \\ -\boldsymbol{a}^{2} & -\boldsymbol{a} \boldsymbol{b}\end{array}\right) .$ To...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}1 & 0 & -2 \\ 3 & -1 & 0 \\ -2 & 1 & 1\end{array}\right], B=\left[\begin{array}{ccc}0 & 5 & -4 \\ -2 & 1 & 3 \\ 1 & 0 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a00e039f4079110b22d247fddf0823b8_l3.png) and
and ![Rendered by QuickLaTeX.com C=\left[\begin{array}{ccc}1 & 5 & 2 \\ -1 & 1 & 0 \\ 0 & -1 & 1\end{array}\right] ;](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dda16b559739c22d0dee0f77fa7c40b0_l3.png) verify that
verify that 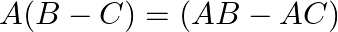
Solution: We have $A=\left(\begin{array}{ccc}1 & 0 & 2 \\ 3 & -1 & 0 \\ -2 & 1 & 1\end{array}\right), B=\left(\begin{array}{ccc}0 & 5 & -4 \\ -2 & 1 & 3 \\ 1...
Verify that 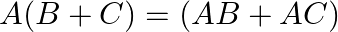 , when
, when ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{cc} 2 & 3 \\ -1 & 4 \\ 0 & 1 \end{array}\right], \mathrm{B}=\left[\begin{array}{cc} 5 & -3 \\ 2 & 1 \end{array}\right] \text { and } \mathrm{C}=\left[\begin{array}{cc} -1 & 2 \\ 3 & 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fd66ff615b29326ba3d097b4946cee2e_l3.png)
Solution: We have $A=\left(\begin{array}{cc}2 & 3 \\ -1 & 4 \\ 0 & 1\end{array}\right), B=\left(\begin{array}{cc}5 & -3 \\ 2 & 1\end{array}\right)$. and...
Verify that 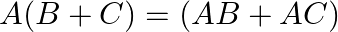 , when
, when ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right], \mathrm{B}=\left[\begin{array}{cc} 2 & 0 \\ 1 & -3 \end{array}\right] \text { and } \mathrm{C}=\left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-65c5d9f1c3d09f9b98677f8ffcad25dc_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ll}\mathbf{1} & \mathbf{2} \\ \mathbf{3} & \mathbf{4}\end{array}\right), \boldsymbol{B}=\left(\begin{array}{cc}\mathbf{2} &...
For the following matrices, verify that 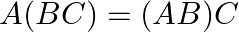 :
: ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ccc} 2 & 3 & -1 \\ 3 & 0 & 2 \end{array}\right], \mathrm{B}=\left[\begin{array}{l} 1 \\ 1 \\ 2 \end{array}\right] \text { and } \mathrm{C}=\left[\begin{array}{ll} 1 & -2 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f267062030e6a4b1a9e0ae96655b75b9_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{2} & \mathbf{3} & \mathbf{- 1} \\ \mathbf{3} & \mathbf{0} & \mathbf{2}\end{array}\right),...
For the following matrices, verify that 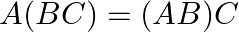 :
: ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{lll} 1 & 2 & 5 \\ 0 & 1 & 3 \end{array}\right], \mathrm{B}=\left[\begin{array}{lll} 2 & 3 & 0 \\ 1 & 0 & 4 \\ 1 & -1 & 2 \end{array}\right] \text { and } \mathrm{C}=\left[\begin{array}{l} 1 \\ 4 \\ 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28076805d7b71c6daa66bcab8ce41845_l3.png)
Solution: We have $A=\left(\begin{array}{lll}1 & 2 & 5 \\ 0 & 1 & 3\end{array}\right), B=\left(\begin{array}{ccc}2 & 3 & 0 \\ 1 & 0 & 4 \\ 1 & -1 &...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}0 & c & -b \\ -c & 0 & a \\ b & -a & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-38b9629a3ecd89b9f213d5de336a84f0_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{lll}a^{2} & a b & a c \\ a b & b^{2} & b c \\ a c & b c & c^{2}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-95fc7f6ea73a57dfb76fa56240b6d2f5_l3.png) . show that
. show that 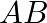 is a zero matrix.
is a zero matrix.
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{0} & \boldsymbol{c} & -\boldsymbol{b} \\ -\boldsymbol{c} & \mathbf{0} & \boldsymbol{a} \\ \boldsymbol{b} &...
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{2} & -\mathbf{3} & -\mathbf{5} \\ -\mathbf{1} & \mathbf{4} & \mathbf{5} \\ \mathbf{1} & -\mathbf{3} &...
Show that 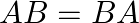 in each of the following cases:
in each of the following cases: ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc} 1 & 3 & -1 \\ 2 & 2 & -1 \\ 3 & 0 & -1 \end{array}\right] \text { and } B=\left[\begin{array}{ccc} -2 & 3 & -1 \\ -1 & 2 & -1 \\ -6 & 9 & -4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7a2b2d708af06466b10968e7314747a5_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{1} & \mathbf{3} & -\mathbf{1} \\ \mathbf{2} & \mathbf{2} & -\mathbf{1} \\ \mathbf{3} & \mathbf{0} &...
Show that 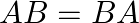 in each of the following cases:
in each of the following cases: ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{lll} 1 & 2 & 1 \\ 3 & 4 & 2 \\ 1 & 3 & 2 \end{array}\right] \text { and } \mathrm{B}=\left[\begin{array}{ccc} 10 & -4 & -1 \\ -11 & 5 & 0 \\ 9 & -5 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f2cf553262923f440cdb2486ff51fdb6_l3.png)
Solution: We have $A=\left(\begin{array}{lll}1 & 2 & 1 \\ 3 & 4 & 2 \\ 1 & 3 & 2\end{array}\right)$ and $B=\left(\begin{array}{ccc}10 & -4 & -1 \\ -11 & 5 & 0...
Show that 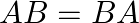 in each of the following cases:
in each of the following cases: ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \text { and } B=\left[\begin{array}{cc} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-de32b04501d491874e21effd827b2a59_l3.png)
Solution: We have $A=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right)$ and $B=\left(\begin{array}{cc}\cos \phi & -\sin \phi \\ \sin \phi...
Show that 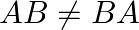 in each of the following cases:
in each of the following cases: ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right] \text { and } \mathrm{B}=\left[\begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4ffeaf0e1df4be603ccf10fb6d6f40b6_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{lll}\mathbf{1} & \mathbf{2} & \mathbf{3} \\ \mathbf{0} & \mathbf{1} & \mathbf{0} \\ \mathbf{1} & \mathbf{1} &...
Show that 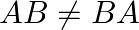 in each of the following cases :
in each of the following cases : ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right] \text { and } B=\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7f5c45bafaa8a499f178625171ba32fc_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{5} & -\mathbf{1} \\ \mathbf{6} & \mathbf{7}\end{array}\right)$ and $\boldsymbol{B}=\left(\begin{array}{ll}\mathbf{2} &...
Compute 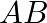 and
and 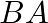 , which ever exists when
, which ever exists when ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{array}\right] \text { and } B=\left[\begin{array}{rrr} 1 & 0 & 1 \\ -1 & 2 & 1 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-279e1d695b832080e5f60bbaf01191b3_l3.png)
Solution: We have $\boldsymbol{B}=\left(\begin{array}{ccc}\mathbf{1} & \mathbf{0} & \mathbf{1} \\ -\mathbf{1} & \mathbf{2} & \mathbf{1}\end{array}\right)$ and...
Compute 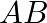 and BA, which ever exists when
and BA, which ever exists when ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll} 1 & 2 & 3 & 4 \end{array}\right] \text { and } B=\left[\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dd6c4ca0935c74e87d91cc74e4077943_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{llll}\mathbf{1} & 2 & 3 & 4\end{array}\right)$ and $\boldsymbol{B}=\left(\begin{array}{l}\mathbf{1} \\ \mathbf{2} \\ \mathbf{3} \\...
Compute AB and BA, which ever exists when ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{rrr} 0 & 1 & -5 \\ 2 & 4 & 0 \end{array}\right] \text { and } \mathrm{B}=\left[\begin{array}{cc} 1 & 3 \\ -1 & 0 \\ 0 & 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-02b69ceb338bd244cfc287cc78e2993a_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{ccc}\mathbf{0} & \mathbf{1} & -\mathbf{5} \\ \mathbf{2} & \mathbf{4} & \mathbf{0}\end{array}\right)$ and...
Compute AB and BA, which ever exists when ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{cc} -1 & 1 \\ -2 & 2 \\ -3 & 3 \end{array}\right] \text { and } \mathrm{B}=\left[\begin{array}{ccc} 3 & -2 & 1 \\ 0 & 1 & 2 \\ -3 & 4 & -5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-499601ef9942d093f177dcd042e96b76_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}-\mathbf{1} & \mathbf{1} \\ -\mathbf{2} & \mathbf{2} \\ -\mathbf{3} & \mathbf{3}\end{array}\right)$ and...
Compute AB and BA, which ever exists when ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc} 2 & -1 \\ 3 & 0 \\ -1 & 4 \end{array}\right] \text { and } B=\left[\begin{array}{cc} -2 & 3 \\ 0 & 4 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-21ad4759d8ac8e3299f333785850143c_l3.png)
Solution: We have $\boldsymbol{A}=\left(\begin{array}{cc}\mathbf{2} & \mathbf{- 1} \\ \mathbf{3} & \mathbf{0} \\ \mathbf{- 1} & \mathbf{4}\end{array}\right)$ and...
If ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}x-y & 2 y \\ 2 y+z & x+y\end{array}\right]=\left[\begin{array}{ll}1 & 4 \\ 9 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2ca4ce3421a2dc3e7599f50fd58c71fa_l3.png) then write the value of
then write the value of 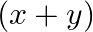
Solution: $\text { If }\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]=\left[\begin{array}{ll} e & f \\ g & h \end{array}\right]$ Therefore $a=e, b=f, c=g, d=h$ It is given...
Find the value of 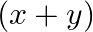 from the following equation :
from the following equation : ![Rendered by QuickLaTeX.com 2\left[\begin{array}{ll} 1 & 3 \\ 0 & \mathrm{x} \end{array}\right]+\left[\begin{array}{ll} \mathrm{y} & 0 \\ 1 & 2 \end{array}\right]=\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fae2ef579b0094ec795f1c62b9a4b3ba_l3.png)
Solution: It is given that $\begin{array}{l} 2\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]+\left[\begin{array}{ll} y & 0 \\ 1 & 2...
Find the value of  and
and  , when
, when
i. ![Rendered by QuickLaTeX.com 2\left[\begin{array}{cc}x & 5 \\ 7 & y-3\end{array}\right]+\left[\begin{array}{cc}3 & -4 \\ 1 & 2\end{array}\right]=\left[\begin{array}{cc}7 & 6 \\ 15 & 14\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b289d871572f69a53ee3333c591b7fdd_l3.png)
Solution: (i) Given $2\left(\begin{array}{lc} x & 5 \\ 7 y-3 \end{array}\right)+\left(\begin{array}{c} 3-4 \\ 12 \end{array}\right)=\left(\begin{array}{cc} 7 & 6 \\ 1514 \end{array}\right)$...
Find the value of  and
and  , when
, when
i. ![Rendered by QuickLaTeX.com \left[\begin{array}{l}\mathrm{x}+\mathrm{y} \\ \mathrm{x}-\mathrm{y}\end{array}\right]=\left[\begin{array}{l}8 \\ 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4f327f4e30d328717ac87c5768d0bd84_l3.png)
ii. ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2 x+5 & 7 \\ 0 & 3 y-7\end{array}\right]=\left[\begin{array}{cc}x-3 & 7 \\ 0 & -5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9bc3080cd3ca5d8961ae81f2e6b07c22_l3.png)
Solution: (i) Given $\left(\begin{array}{l}\boldsymbol{x}+\boldsymbol{y} \\ \boldsymbol{x}-\boldsymbol{y}\end{array}\right)=\left(\begin{array}{l}8 \\ \mathbf{4}\end{array}\right)$. By equality of...
If ![Rendered by QuickLaTeX.com A=\operatorname{diag}[2,-5,9], B=\operatorname{diag}[-3,7,14]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e915667c4dc298d0e9ed08f771e99b84_l3.png) and
and ![Rendered by QuickLaTeX.com C=\operatorname{diag}[4,-6,3]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-274f356305cd7bdb13df4255156b7ef6_l3.png) , find:
, find:
(i) 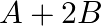
(ii) 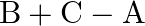
Solution: If $Z=\operatorname{diag}[a, b, c]$, then it can be written as $Z=\left[\begin{array}{lll} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{array}\right]$ Therefore, $A+2...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rrr}1 & -3 & 2 \\ 2 & 0 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f1d0bfe594db55e6d03941a543e5b71b_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{ccc}2 & -1 & -1 \\ 1 & 0 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bad6f5c51302ce532530299b88d44da6_l3.png) , find a matrix
, find a matrix  such that
such that 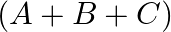 is a zero matrix.
is a zero matrix.
Solution: It is given that $A+B+C$ is zero matrix i.e $A+B+C=0$ $\begin{array}{l} {\left[\begin{array}{ccc} 1 & -3 & 2 \\ 2 & 0 & 2 \end{array}\right]+\left[\begin{array}{ccc} 2...
Find the matrix 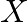 such that
such that 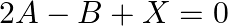 where
where ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & 1 \\ 0 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-687ea49b624f69078701c50bdfe70143_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}-2 & 1 \\ 0 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-327689b71c17725ba5fadd5f6c04b7ea_l3.png)
Solution: It is given that $2 A-B+X=0$ $\begin{array}{l} 2\left(\left[\begin{array}{ll} 3 & 1 \\ 0 & 2 \end{array}\right]\right)-\left[\begin{array}{cc} -2 & 1 \\ 0 & 3...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}-2 & 3 \\ 4 & 5 \\ 1 & -6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1a126b89e46fb513ab316d9ddf765f2_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}5 & 2 \\ -7 & 3 \\ 6 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ea823875b60d35239b7a90f86c04d7b6_l3.png) , find a matrix
, find a matrix  such that
such that 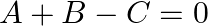
Solution: It is given that $A+B-C=0$ $\begin{array}{c} {\left[\begin{array}{cc} -2 & 3 \\ 4 & 5 \\ 1 & -6 \end{array}\right]+\left[\begin{array}{cc} 5 & 2 \\ -7 & 3 \\ 6 & 4...
Find matrix 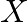 , if
, if ![Rendered by QuickLaTeX.com \left[\begin{array}{rrr}3 & 5 & -9 \\ -1 & 4 & -7\end{array}\right]+X=\left[\begin{array}{lll}6 & 2 & 3 \\ 4 & 8 & 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-45e666fb26d68da37727a27b2abe54f0_l3.png)
Solution: It is given that $\left[\begin{array}{ccc}3 & 5 & -9 \\ -1 & 4 & -7\end{array}\right]+x=\left[\begin{array}{lll}6 & 2 & 3 \\ 4 & 8 & 6\end{array}\right]$...
Find matrices  and
and  , if
, if ![Rendered by QuickLaTeX.com 2 A-B=\left[\begin{array}{rrr}6 & -6 & 0 \\ -4 & 2 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7c7e70a825c505f4ed47602a40feb33a_l3.png) and
and ![Rendered by QuickLaTeX.com 2 B+A=\left[\begin{array}{ccc}3 & 2 & 5 \\ -2 & 1 & -7\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-97bab0d2cf485a48b9cadb26dc60dbb6_l3.png)
Solution: $\operatorname{Add} 2(2 A-B)$ and $(2 B+A)$ $\begin{array}{l} 2(2 A-B)+(2 B+A)=2\left(\left[\begin{array}{ccc} 6 & -6 & 0 \\ -4 & 2 & 1...
Find matrices  and
and  , if
, if ![Rendered by QuickLaTeX.com A+B=\left[\begin{array}{ccc}1 & 0 & 2 \\ 5 & 4 & -6 \\ 7 & 3 & 8\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3a87601979fb533a239d62337a5b2064_l3.png) and
and ![Rendered by QuickLaTeX.com A-B=\left[\begin{array}{ccc}-5 & -4 & 8 \\ 11 & 2 & 0 \\ -1 & 7 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-58cb7bbac0f7ccbeaeb8025170c9380e_l3.png)
Solution: Add $(A+B)$ and $(A-B)$ We obtain $(A+B)+(A-B)=\left[\begin{array}{ccc}1 & 0 & 2 \\ 5 & 4 & -6 \\ 7 & 3 & 8\end{array}\right]+\left[\begin{array}{ccc}-5 & -4...
If ![Rendered by QuickLaTeX.com 5 \mathrm{~A}=\left[\begin{array}{ccc}5 & 10 & -15 \\ 2 & 3 & 4 \\ 1 & 0 & -5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-68173ac372a0be08a045f2efa000c776_l3.png) , find
, find 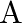
Solution: $5 A=\left[\begin{array}{ccc}5 & 10 & -15 \\ 2 & 3 & 4 \\ 1 & 0 & -5\end{array}\right]$ $A=\left[\begin{array}{ccc}\frac{5}{5} & \frac{10}{5} &...
Let ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}0 & 1 & -2 \\ 5 & -1 & -4\end{array}\right], B=\left[\begin{array}{ccc}1 & -3 & -1 \\ 0 & -2 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-41e2731669cc626117fcfaab4c782d70_l3.png) and
and ![Rendered by QuickLaTeX.com C=\left[\begin{array}{ccc}2 & -5 & 1 \\ -4 & 0 & 6\end{array}\right] .](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ec6db1baabfa8122c2209e13ff3fac41_l3.png) Compute
Compute 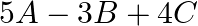
Solution: $\begin{array}{l} \left.5 A-3 B+4 C=5\left(\left[\begin{array}{ccc} 0 & 1 & -2 \\ 5 & -1 & -4 \end{array}\right]\right)-3\left(\begin{array}{ccc} 1 & -3 & -1 \\ 0...
Let ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}2 & 4 \\ 3 & 2\end{array}\right], B=\left[\begin{array}{cc}1 & 3 \\ -2 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a7bc1c4d1eeefbbc4f83e854a1687521_l3.png) and
and ![Rendered by QuickLaTeX.com C=\left[\begin{array}{cc}-2 & 5 \\ 3 & 4\end{array}\right] .](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8bd7890a3a96a4c97189a908536ad3df_l3.png) Find:
Find:
i. 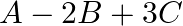
Solution: $\begin{array}{l} \text { i. } A-2 B+3 C \\ \text { A- } 2 B+3 C=\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]-2\left(\left[\begin{array}{cc} 1 & 3 \\ -2 & 5...
Let ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}2 & 4 \\ 3 & 2\end{array}\right], B=\left[\begin{array}{cc}1 & 3 \\ -2 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a7bc1c4d1eeefbbc4f83e854a1687521_l3.png) and
and ![Rendered by QuickLaTeX.com C=\left[\begin{array}{cc}-2 & 5 \\ 3 & 4\end{array}\right] .](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8bd7890a3a96a4c97189a908536ad3df_l3.png) Find:
Find:
i. 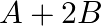
ii. B – 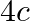
Solution: i. $\begin{array}{l} A+2 B=\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]+2\left(\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right]\right) \\...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}3 & 1 & 2 \\ 1 & 2 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-31a9f285753e96665b1043f971261649_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{ccc}-2 & 0 & 4 \\ 5 & -3 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2db0d1cb1cd62becc5703078ca3469a4_l3.png) , find
, find 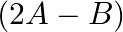
Solution: $\begin{array}{l} 2 A=2\left(\left[\begin{array}{ccc} 3 & 1 & 2 \\ 1 & 2 & -3 \end{array}\right]\right) \\ =\left[\begin{array}{ccc} 6 & 2 & 4 \\ 2 & 4 & -6...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3 & 5 \\ -2 & 0 \\ 6 & -1\end{array}\right], B=\left[\begin{array}{cc}-1 & -3 \\ 4 & 2 \\ -2 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-66f7d37c6136b09956a37ec4bd7b2766_l3.png) and
and ![Rendered by QuickLaTeX.com C=\left[\begin{array}{cc}0 & 2 \\ 3 & -4 \\ 1 & 6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e8b8119fe41187456a97ee682923debd_l3.png) , verify that
, verify that 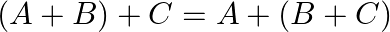
Solution: $\begin{array}{l} (A+B)+C=\left(\left[\begin{array}{cc} 3 & 5 \\ -2 & 0 \\ 6 & -1 \end{array}\right]+\left[\begin{array}{cc} -1 & -3 \\ 4 & 2 \\ -2 & 3...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}2 & -3 & 5 \\ -1 & 0 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c18faf5289add2dd71e42331e8e0f3fb_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{ccc}3 & 2 & -2 \\ 4 & -3 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ac37f82b6c044fe5ac67eaa50137a95c_l3.png) , verify that
, verify that 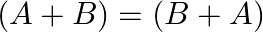
Solution: $\begin{array}{l} A+B=\left[\begin{array}{ccc} 2 & -3 & 5 \\ -1 & 0 & 3 \end{array}\right]+\left[\begin{array}{ccc} 3 & 2 & -2 \\ 4 & -3 & 1...
Construct a  matrix whose elements are given by
matrix whose elements are given by 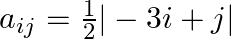
Solution: It is a (3 $x 4)$ matrix. Therefore, it has 3 rows and 4 columns. Given that $a_{i j}=\frac{|-a \|+| l}{2}$ Therefore, $a_{11}=1 . a_{12}=\frac{1}{2}, a_{13}=0, a_{13}=\frac{1}{2}$...
Construct a  matrix whose elements are
matrix whose elements are 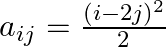
Solution: It is a $(2 \times 3)$ matrix. Therefore, it has 2 rows and 3 columns. Given that $a_{i j}=\frac{\left(t-2 \rho^{2}\right.}{2}$ Therefore, $a_{11}=\frac{1}{2}, a_{12}=\frac{9}{2},...
Construct a  matrix whose elements are
matrix whose elements are 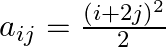
Solution: It is a $(2 \times 2)$ matrix. So, it has 2 rows and 2 columns. Given that $a_{i j}=\frac{(i+2 j)^{2}}{2}$ Therefore, $a_{11}=\frac{9}{2}, a_{12}=\frac{25}{2}$. $a_{21}=8 . a_{22}=18$...
Construct a  matrix whose elements are given by
matrix whose elements are given by 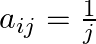
Solution: It is $(4 \times 3)$ matrix. Therefore it has 4 rows and 3 columns Given that$a_{i j}=\frac{i}{j}$ Therefore, $a_{11}=1 . a_{12}=\frac{1}{2}, a_{13}=\frac{1}{3}$ $\begin{array}{l}...
Construct a  matrix whose elements are given by
matrix whose elements are given by 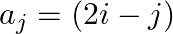
Solution: It is given that: $a_{i j}=(2 \mid-j)$ Now, $a_{11}=(2 \times 1-1)=2-1=1$ $\begin{array}{l} a_{12}=2 \times 1-2=2-2=0 \\ a_{21}=2 \times 2-1=4-1=3 \\ a_{22}=2 \times 2-2=4-2=2 \\ a_{31}=2...
Find all possible orders of matrices having 7 elements.
Solution: No. of entries $=($ No. of rows) $x$ (No. of columns) $=7$ If order is $(\mathrm{a} \times \mathrm{b})$ then, No. of entries = $\mathrm{a} \times \mathrm{b}$ Therefore now a $x b=7$ (in...
If a matrix has 18 elements, what are the possible orders it can have?
Solution: No. of entries $=$ (No. of rows) $x$ (No. of columns) $=18$ If order is $(a \times b)$ then, No. of entries = $a \times b$ Therefore now $a \times b=18$ (in this case) Possible cases are...
Write the order of each of the following matrices:
i. ![Rendered by QuickLaTeX.com E=\left[\begin{array}{c}-2 \\ 3 \\ 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d6b4b616a18471e5e1da412182f3cfc8_l3.png)
ii, ![Rendered by QuickLaTeX.com F=[6]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f1b7ee74e8d279705a2649b7c1427d2a_l3.png)
Solution: i. $E=\left[\begin{array}{c}-2 \\ 3 \\ 0\end{array}\right]$ Order of matrix $=$ Number of rows $x$ Number of columns $\begin{array}{l} =(3 \times 1) \\ \text { ii, } F=[6] \end{array}$...
Write the order of each of the following matrices:
i. ![Rendered by QuickLaTeX.com \mathrm{C}=\left[\begin{array}{lll}7-\sqrt{2} & 5 & 0\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2eb7b03611cf5621ee3d31e5a86b8236_l3.png)
ii. ![Rendered by QuickLaTeX.com \mathrm{D}=[8-3]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-40c5e53abc7a937eeaeba1db8b071d85_l3.png)
Solution: i. $C=[7-\sqrt{2} \quad 5 \quad 0]$ Order of matrix $=$ Number of rows $x$ Number of columns $=(1 \times 4)$ ii. $D=[8-3]$ Order of matrix $=$ Number of rows $x$ Number of columns $=(1...
Write the order of each of the following matrices: i. ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cccc}3 & 5 & 4 & -2 \\ 0 & \sqrt{3} & -1 & \frac{4}{9}\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f969e23c5c5287707729c241fef79e75_l3.png) ii.
ii. ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}6 & -5 \\ \frac{1}{2} & \frac{3}{4} \\ -2 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ec1233b19429c118c718399789e144a6_l3.png)
Solution: i. $A=\left[\begin{array}{cccc}3 & 5 & 4 & -2 \\ 0 & \sqrt{3} & -1 & \frac{4}{9}\end{array}\right]$ Order of matrix $=$ Number of rows $x$ Number of columns $=(2...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cccc}5 & -2 & 6 & 1 \\ 7 & 0 & 8 & -3 \\ \sqrt{2} & \frac{3}{5} & 4 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1db7451bba1582e7fdf8b71d478bfc78_l3.png) then write
then write
i. the elements 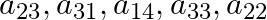 of
of  .
.
Solution: (i) $a_{i j}=$ element of $t^{\text {th }}$ row and $j^{\text {th }}$ column $\begin{array}{l} a_{23}=8 \\ a_{31}=\sqrt{2} \\ a_{14}=1 \\ a_{33}=4 \\ a_{22}=0 \end{array}$
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cccc}5 & -2 & 6 & 1 \\ 7 & 0 & 8 & -3 \\ \sqrt{2} & \frac{3}{5} & 4 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1db7451bba1582e7fdf8b71d478bfc78_l3.png) then write
then write
i. the order of the matrix  ,
,
ii. the number of all entries in  ,
,
Solution: (i) Order of matrix $=$ Number of rows $x$ Number of columns $=(3 \times 4)$ (ii) Number of entries = (Number of rows) $x$ (Number of columns) $=3 \times 4$ $=12$
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cccc}5 & -2 & 6 & 1 \\ 7 & 0 & 8 & -3 \\ \sqrt{2} & \frac{3}{5} & 4 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1db7451bba1582e7fdf8b71d478bfc78_l3.png) then write
then write
i. the number of rows in  ,
,
ii. the number of columns in  ,
,
Solution: (i) Number of rows $=3$ (ii) Number of columns = 4

![Rendered by QuickLaTeX.com \text { If } A=\left[\begin{array}{ccc} 2 & -3 & -5 \\ -1 & 4 & 5 \\ 1 & -3 & -4 \end{array}\right] \text { and } B=\left[\begin{array}{ccc} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{array}\right] \text {, shown that } A B=A \text { and } B A=B \text {. }](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f7bbfb06d7327fe19b0ea3748a21ef6c_l3.png)