(v) Number of favorable outcomes for a diamond or a spade = 13 + 13 = 26 So, number of favorable outcomes = 26 Hence, P(getting a diamond or a spade) = 26/52 = 1/2
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting: (iii) the jack or the queen of the hearts (iv) a diamond
(iii) Favorable outcomes for jack or queen of hearts = 1 jack + 1 queen So, the number of favorable outcomes = 2 Hence, P(jack or queen of hearts) = 2/52 = 1/26 (iv) Number of favorable outcomes for...
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting: (i) a queen of red color (ii) a black face card
Solution: We have, Total possible outcomes = 52 (i) Number queens of red color = 2 Number of favorable outcomes = 2 Hence, P(queen of red color) = 2/52 (ii) Number of black cards = 26 Number of...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (v) a number less than or equal to 9 (vi) a number between 3 and 11
(v) Favorable outcomes for a number less than or equal to 9 are 1, 2, 3, 4, 5, 6, 7, 8, 9 So, number of favorable outcomes = 9 Hence, P(the pointer will be at a number less than or equal to 9) =...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (iii) a prime number (iv) a number greater than 8
(iii) Favorable outcomes for a prime number are 2, 3, 5, 7, 11 So, number of favorable outcomes = 5 Hence, P(the pointer will be at a prime number) = 5/12 (iv) Favorable outcomes for a number...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (i) 6 (ii) an even number
Solution: We have, Total number of possible outcomes = 12 (i) Number of favorable outcomes for 6 = 1 Hence, P(the pointer will point at 6) = 1/12 (ii) Favorable outcomes for an even number are 2, 4,...
A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin: (i) will be a Re 1 coin? (ii) will not be a Rs 2 coin? (iii) will neither be a Rs 5 coin nor be a Re 1 coin?
(iii) Number of favourable outcomes for neither Re 1 nor Rs 5 coins = Number of favourable outcomes for Rs 2 coins = 50 = n(E) Hence, probability (neither Re 1 nor Rs 5 coin) = n(E)/ n(S) = 50/100 =...
A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin: (i) will be a Re 1 coin? (ii) will not be a Rs 2 coin?
Solution: We have, Total number of coins = 20 + 50 + 30 = 100 So, the total possible outcomes = 100 = n(S) (i) Number of favourable outcomes for Re 1 coins = 30 = n(E) Probability (Re 1 coin) =...
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be: (iii) white or green?
(iii) Number of favorable outcomes for white or green ball = 16 + 8 = 24 = n(E) Hence, probability for drawing a white or green ball = n(E)/ n(S) = 24/34 = 12/17
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be: (i) not red? (ii) neither red nor green?
Solution: Total number of possible outcomes = 10 + 16 + 8 = 34 balls So, n(S) = 34 (i) Favorable outcomes for not a red ball = favorable outcomes for white or green ball So, number of favorable...
The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday?
Solution: We know that, P(do not have the same birthday) + P(have same birthday) = 1 0.897 + P(have same birthday) = 1 Thus, P(have same birthday) = 1 – 0.897 P(have same birthday) =...
A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is: (i) black (ii) red
Solution: We have, Total possible outcomes = number of red balls. (i) Number of favourable outcomes for black balls = 0 Hence, P(black ball) = 0 (ii) Number of favourable outcomes for red balls =...
If P(E) = 0.59; find P(not E)
Solution: We know that, P(E) + P(not E) = 1 So, 0.59 + P(not E) = 1 Hence, P(not E) = 1 – 0.59 = 0.41
Which of the following cannot be the probability of an event? (iii) 37% (iv) -2.4
(iii) As 0 ≤ 37 % = (37/100) ≤ 1 Thus, 37 % can be a probability of an event. (iv) As -2.4 < 0 Thus, -2.4 cannot be a probability of an event.
Which of the following cannot be the probability of an event? (i) 3/7 (ii) 0.82
Solution: We know that probability of an event E is 0 ≤ P(E) ≤ 1 (i) As 0 ≤ 3/7 ≤ 1 Thus, 3/7 can be a probability of an event. (ii) As 0 ≤ 0.82 ≤ 1 Thus, 0.82 can be a probability of an...
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is:(iii) less than or equal to 12
(iii) All the outcomes are favourable to the event E = ‘sum of two numbers ≤ 12’. Thus, P(E) = n(E)/ n(S) = 36/36 = 1
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is: (i) 8 (ii) 13
Solution: We have, the number of possible outcomes = 6 × 6 = 36. (i) The outcomes favourable to the event ‘the sum of the two numbers is 8’ = E = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)} The number...
In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that: (i) it is acceptable to a trader who accepts only a good shirt? (ii) it is acceptable to a trader who rejects only a shirt with major defects?
Solution: We have, Total number of shirts = 50 Total number of elementary events = 50 = n(S) (i) As, trader accepts only good shirts and number of good shirts = 44 Event of accepting good shirts =...
In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds?
Solution: Total result = 0 sec to 40 sec Total possible outcomes = 40 So, n(S) = 40 Favourable results = 0 sec to 15 sec Favourable outcomes = 15 So, n(E) = 15 Hence, the probability that the music...
All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting:(iii) a black card
(iii) Number of black cards left = 23 cards (13 club + 10 spade) Event of drawing a black card = E = 23 So, n(E) = 23 Hence, probability of drawing a black card = n(E)/ n(S) = 23/49
All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting: (i) a black face card (ii) a queen
Solution: We have, Total number of cards = 52 If 3 face cards of spades are removed Then, the remaining cards = 52 – 3 = 49 = number of possible outcomes So, n(S) = 49 (i) Number of black face cards...
A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is: (i) white (ii) neither red nor white.
Solution: We have, Total number of balls in the box = 7 + 8 + 5 = 20 balls Total possible outcomes = 20 = n(S) (i) Event of drawing a white ball = E = number of white balls = 5 So, n(E) = 5 Hence,...
A and B are friends. Ignoring the leap year, find the probability that both friends will have: (i) different birthdays? (ii) the same birthday?
Solution: Out of the two friends, A’s birthday can be any day of the year. Now, B’s birthday can also be any day of 365 days in the year. We assume that these 365 outcomes are equally likely. So,...
In a match between A and B: (i) the probability of winning of A is 0.83. What is the probability of winning of B? (ii) the probability of losing the match is 0.49 for B. What is the probability of winning of A?
Solution: (i) We know that, The probability of winning of A + Probability of losing of A = 1 And, Probability of losing of A = Probability of winning of B Therefore, Probability of winning of A +...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is:(v) a card with number less than 8 (vi) a card with number between 2 and 9
(v) Numbers less than 8 = { 2, 3, 4, 5, 6, 7} Event of drawing a card with number less than 8 = E = {6H cards, 6D cards, 6S cards, 6C cards} So, n(E) = 24 Thus, probability of drawing a card with...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is: (iii) a queen of black card (iv) a card with number 5 or 6
(iii) Event of drawing a queen of black colour = {Q(spade), Q(club)} = E So, n(E) = 2 Thus, probability of drawing a queen of black colour = n(E)/ n(S) = 2/52 = 1/26 (iv) Event of drawing a card...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is: (i) a face card (ii) not a face card
Solution: We have, the total number of possible outcomes = 52 So, n(S) = 52 (i) No. of face cards in a deck of 52 cards = 12 (4 kings, 4 queens and 4 jacks) Event of drawing a face cards = E = (4...
A dice is thrown once. What is the probability of getting a number: (i) greater than 2? (ii) less than or equal to 2?
Solution: The number of possible outcomes when dice is thrown = {1, 2, 3, 4, 5, 6} So, n(S) = 6 (i) Event of getting a number greater than 2 = E = {3, 4, 5, 6} So, n(E) = 4 Thus, probability of...
A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is: (iii) not yellow (iv) neither yellow nor red
(iii) Probability of not drawing a yellow ball = 1 – Probability of drawing a yellow ball Thus, probability of not drawing a yellow ball = 1 – 1/8 = (8 – 1)/ 8 = 7/8 (iv) Neither yellow ball nor red...
A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is: (i) yellow (ii) red
Solution: The total number of balls in the bag = 3 + 4 + 1 = 8 balls So, the number of possible outcomes = 8 = n(S) (i) Event of drawing a yellow ball = {Y} So, n(E) = 1 Thus, probability of drawing...
If two coins are tossed once, what is the probability of getting: (iii) both heads or both tails.
(iii) E = event of getting both heads or both tails = {HH, TT} n(E) = 2 Hence, probability of getting both heads or both tails = n(E)/ n(S) = 2/4 = ½
If two coins are tossed once, what is the probability of getting: (i) both heads. (ii) at least one head.
Solution: We know that, when two coins are tossed together possible number of outcomes = {HH, TH, HT, TT} So, n(S) = 4 (i) E = event of getting both heads = {HH} n(E) = 1 Hence, probability of...
A pair of dice is thrown. Find the probability of getting a sum of 10 or more, if 5 appears on the first die.
Solution: In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6} So, n(S) = 6 For two dice, n(S) = 6 x 6 = 36 Favorable cases where the sum is 10 or more with 5 on 1st die = {(5, 5), (5,...
A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?
Solution: We know that, Number of pages in the book = 85 Number of possible outcomes = n(S) = 85 Out of 85 pages, pages that sum up to 8 = {8, 17, 26, 35, 44, 53, 62, 71, 80} So, pages that sum up...
A die is thrown once. Find the probability of getting a number: (iii) less than 8 (iv) greater than 6
(iii) On a dice, numbers less than 8 = {1, 2, 3, 4, 5, 6} So, n(E) = 6 Hence, probability of getting a number less than 8 = n(E)/ n(S) = 6/6 = 1 (iv) On a dice, numbers greater than 6 = 0 So, n(E) =...
A die is thrown once. Find the probability of getting a number: (i) less than 3 (ii) greater than or equal to 4
Solution: We know that, In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6} So, n(S) = 6 (i) On a dice, numbers less than 3 = {1, 2} So, n(E) = 2 Hence, probability of getting a number...
From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of: (iii) 3 and 5 (iv) 3 or 5
(iii) From numbers 1 to 25, there is only one number which is multiple of 3 and 5 i.e. {15} So, favorable number of events = n(E) = 1 Hence, probability of selecting a card with a multiple of 3 and...
From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of: (i) 3 (ii) 5
Solution: We know that, there are 25 cards from which one card is drawn. So, the total number of elementary events = n(S) = 25 (i) From numbers 1 to 25, there are 8 numbers which are multiple of 3...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (v) less than 48
(v) From numbers 1 to 100, there are 47 numbers which are less than 48 i.e. {1, 2, ……….., 46, 47} So, favorable number of events = n(E) = 47 Hence, probability of selecting a card with a number less...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (iii) between 40 and 60 (iv) greater than 85
(iii) From numbers 1 to 100, there are 19 numbers which are between 40 and 60 i.e. {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59} So, favorable number of events = n(E)...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (i) a multiple of 5 (ii) a multiple of 6
Solution: We kwon that, there are 100 cards from which one card is drawn. Total number of elementary events = n(S) = 100 (i) From numbers 1 to 100, there are 20 numbers which are multiple of 5...
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be:(iii) an even number and a multiple of 3 (iv) an even number or a multiple of 3
(iii) From numbers 2 to 10, there is one number which is an even number as well as multiple of 3 i.e. 6 So, favorable number of events = n(E) = 1 Hence, probability of selecting a card with a number...
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be: (i) an even number (ii) a multiple of 3
Solution: We know that, there are totally 9 cards from which one card is drawn. Total number of elementary events = n(S) = 9 (i) From numbers 2 to 10, there are 5 even numbers i.e. 2, 4, 6, 8, 10...
In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of: (i) winning of Geeta (ii) not winning of Ritu
Solution: (i) Winning of Geeta is a complementary event to winning of Ritu Thus, P(winning of Ritu) + P(winning of Geeta) = 1 P(winning of Geeta) = 1 – P(winning of Ritu) P(winning of Geeta) =...
(i) If A and B are two complementary events then what is the relation between P(A) and P(B)? (ii) If the probability of happening an event A is 0.46. What will be the probability of not happening of the event A?
Solution: (i) Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1. P(A) + P(B) = 1 (ii) P(A) = 0.46 Let P(B) be...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will:(v) be a face card of red colour
(v) There are 26 red cards in a deck, and 6 of these cards are face cards (2 kings, 2 queens and 2 jacks). The number of favourable outcomes for the event of drawing a face card of red color = 6...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will: (i) be a black card. (ii) not be a red card. (iii) be a red card. (iv) be a face card.
(iii) Number of red cards in a deck = 26 The number of favourable outcomes for the event of drawing a red card = 26 Then, probability of drawing a red card = 26/52 = ½ (iv) There are 52 cards...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will: (i) be a black card. (ii) not be a red card.
Solution: We know that, Total number of cards = 52 So, the total number of outcomes = 52 There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and diamond are...
In a single throw of a die, find the probability that the number: (iii) will be an odd number.
(iii) If E = event of getting an odd number = {1, 3, 5} So, n(E) = 3 Then, probability of a getting an odd number = n(E)/ n(s) = 3/6 = ½
In a single throw of a die, find the probability that the number: (i) will be an even number. (ii) will not be an even number.
Solution: Here, the sample space = {1, 2, 3, 4, 5, 6} n(s) = 6 (i) If E = event of getting an even number = {2, 4, 6} n(E) = 3 Then, probability of a getting an even number = n(E)/ n(s) = 3/6 = ½...
In a single throw of a die, find the probability of getting a number: (iii) not greater than 4.
(iii) E = event of getting a number not greater than 4 = {1, 2, 3, 4} So, n (E) = 4 Then, probability of getting a number not greater than 4 = n(E)/ n(s) = 4/6 = 2/3
In a single throw of a die, find the probability of getting a number: (i) greater than 4. (ii) less than or equal to 4.
Solution: Here, the sample space = {1, 2, 3, 4, 5, 6} So, n (s) = 6 (i) If E = event of getting a number greater than 4 = {5, 6} So, n (E) = 2 Then, probability of getting a number greater than 4 =...
. A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:(v) not a black ball
(v) There are 3 + 2 = 5 balls which are not black So, the number of favourable outcomes = 5 Thus, P(getting a white ball) = 5/10 = ½
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (iii) a white ball. (iv) not a red ball.
(iii) There are 3 white balls So, the number of favourable outcomes = 3 Thus, P(getting a white ball) = 3/10 = 3/10 (iv) There are 3 + 5 = 8 balls which are not red So, the number of favourable...
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (i) a black ball. (ii) a red ball
Solution: Total number of balls = 3 + 5 + 2 = 10 So, the total number of possible outcomes = 10 (i) There are 5 black balls So, the number of favourable outcomes = 5 Thus, P(getting a black ball) = ...
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (i) a black ball. (ii) a red ball
Solution: Total number of balls = 3 + 5 + 2 = 10 So, the total number of possible outcomes = 10 (i) There are 5 black balls So, the number of favourable outcomes = 5 Thus, P(getting a black ball) = ...
1. A coin is tossed once. Find the probability of: (i) getting a tail (ii) not getting a tail
Solution: Here, the sample space = {H, T} i.e. n(S) = 2 (i) If A = Event of getting a tail = {T} Then, n(A) = 1 Hence, the probability of getting a tail = n(A)/ n(S) = 1/2 (ii) Not getting a tail As...
Determine P (E|F) in: A coin is tossed three times, where (i) 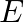 : head on third toss,
: head on third toss, 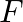 : heads on first two tosses (ii)
: heads on first two tosses (ii) 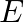 : at least two heads,
: at least two heads, 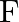 : at most two heads (iii)
: at most two heads (iii)  : at most two tails,
: at most two tails, 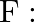 at least one tail
at least one tail
Solution: The sample space of the given experiment will be: S={HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} (i) Given that, E: head-on third toss And F: heads on first two tossesSo writing the sample...
