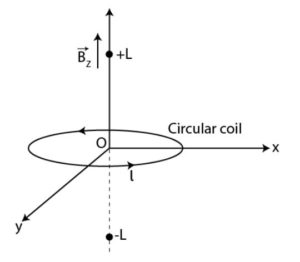
a) A circular current-carrying loop’s magnetic field is given as
![]()
It is a L function that increases monotonically.
b) The Amperian loop is defined as follows:
![]()
c) The magnetic field at the circular coil’s axis is provided by 0I.
d) When a circular coil is swapped out for a square coil, the result is
![]()

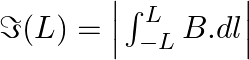 a) show that
a) show that