The sample space for the experiment in question is shown in the table below.
![]()
Let ![]() be the event that ‘the coin shows a tail’ and
be the event that ‘the coin shows a tail’ and ![]() be the event that ‘at least one die shows a 3 ‘.
be the event that ‘at least one die shows a 3 ‘.
![]() and
and ![]()
![]() (i)
(i)
Now, we know that by definition of conditional probability, 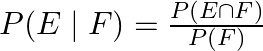
![]()
![]()
