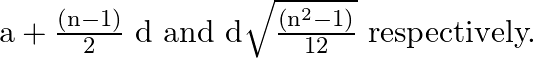Login/Sign Up
Home » Determine mean and standard deviation of first terms of an A.P. whose first term is a and common difference is .
Determine mean and standard deviation of first n terms of an A.P. whose first term is a and common difference is \mathrm{d}.
CBSE | Class 11 | Maths | NCERT Exemplar | Statistics
Determine mean and standard deviation of first n terms of an A.P. whose first term is a and common difference is \mathrm{d}.

Solution:

Given that the first n terms of an A.P. whose first term is a and common difference is d Now we have to find mean and standard deviation

Given AP in tabular form is shown below,

    \[\begin{tabular}{|l|l|l|} \hline$x_{i}$ & $d_{i}=x_{i}-a$ & $d_{i}^{2}$ \\ \hline$a$ & 0 & 0 \\ \hline$a+d$ & $d$ & $d^{2}$ \\ \hline$a+2 d$ & $2 d$ & $4 d^{2}$ \\ \hline$a+3 d$ & $3 d$ & $9 d^{2}$ \\ \hline$-$ & $-$ & $-$ \\ \hline$a+(n-1) d$ & $(n-1) d$ & $(n-1)^{2} d^{2}$ \\ \hline \end{tabular}\]

Assumed a as mean.

Given that the AP have n terms. And it is known that the sum of all the terms of AP can be written as,

\sum \mathrm{x}_{\mathrm{i}}=\frac{\mathrm{n}}{2}[2 \mathrm{a}+(\mathrm{n}-1) \mathrm{d}]

Calculate the actual mean,

\overline{\mathrm{x}}=\frac{\sum \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}

Substitute the corresponding values,

\bar{x}=\frac{\frac{n}{2}[2 a+(n-1) d]}{n}

Above eq. can be written as

\begin{aligned} &\bar{x}=\frac{[2 a+(n-1) d]}{2} \\ &\bar{x}=a+\frac{[(n-1) d]}{2} \\ &\bar{x}=a+\frac{(n-1)}{2} d \end{aligned}

The other two columns sums, i.e. _{\text {. }}

\sum d_{i}=\sum\left(x_{i}-a\right)=d[1+2+3+\cdots+(n-1)]=d\left(\frac{n(n-1)}{2}\right)

\sum \mathrm{d}_{\mathrm{i}}^{2}=\sum\left(\mathrm{x}_{\mathrm{i}}-\mathrm{a}\right)^{2}=\mathrm{d}^{2}\left[1^{2}+2^{2}+3^{2}+\cdots+(\mathrm{n}-1)^{2}\right]=\mathrm{d}^{2}\left(\frac{\mathrm{n}(\mathrm{n}-1)(2 \mathrm{n}-1)}{6}\right)

The standard deviation is given by,

\sigma=\sqrt{\frac{\sum\left(\mathrm{x}_{\mathrm{i}}-\mathrm{a}\right)^{2}}{\mathrm{n}}-\left(\frac{\sum\left(\mathrm{x}_{\mathrm{i}}-\mathrm{a}\right)}{\mathrm{n}}\right)^{2}}

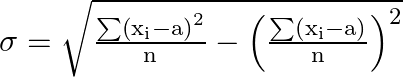
Substitute the corresponding values,

\begin{aligned} &\sigma=\sqrt{\frac{\mathrm{d}^{2}\left(\frac{\mathrm{n}(\mathrm{n}-1)(2 \mathrm{n}-1)}{6}\right)}{\mathrm{n}}-\left(\frac{\mathrm{d}\left(\frac{\mathrm{n}(\mathrm{n}-1)}{2}\right)}{\mathrm{n}}\right)^{2}} \\ &\sigma=\sqrt{\mathrm{d}^{2}\left(\frac{\mathrm{n}(\mathrm{n}-1)(2 \mathrm{n}-1)}{6 \mathrm{n}}\right)-\mathrm{d}^{2}\left(\frac{\mathrm{n}^{2}(\mathrm{n}-1)^{2}}{4 \mathrm{n}^{2}}\right)} \end{aligned}

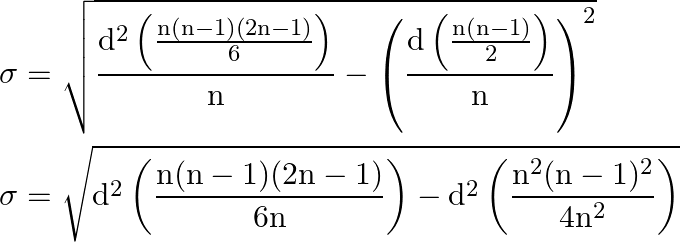
Cancel the like terms,

\sigma=\sqrt{\mathrm{d}^{2}\left(\frac{(\mathrm{n}-1)(2 \mathrm{n}-1)}{6}\right)-\mathrm{d}^{2}\left(\frac{(\mathrm{n}-1)^{2}}{4}\right)}

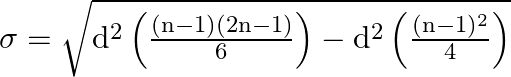
Take out the common terms

\sigma=\sqrt{\left(\frac{\mathrm{d}^{2}(\mathrm{n}-1)}{2}\right)\left(\frac{(2 \mathrm{n}-1)}{3}-\frac{\mathrm{n}-1}{2}\right)}

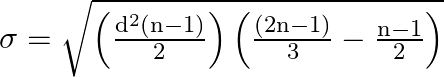
Taking the LCM,

\begin{aligned} &\sigma=\sqrt{\left(\frac{\mathrm{d}^{2}(\mathrm{n}-1)}{2}\right)\left(\frac{2(2 \mathrm{n}-1)-3(\mathrm{n}-1)}{6}\right)} \\ &\sigma=\sqrt{\left(\frac{\mathrm{d}^{2}(\mathrm{n}-1)}{2}\right)\left(\frac{4 \mathrm{n}-2-3 \mathrm{n}+3}{6}\right)} \\ &\sigma=\sqrt{\left(\frac{\mathrm{d}^{2}(\mathrm{n}-1)}{2}\right)\left(\frac{\mathrm{n}+1}{6}\right)} \\ &\sigma=\mathrm{d} \sqrt{\frac{\left(\mathrm{n}^{2}-1\right)}{12}} \end{aligned}

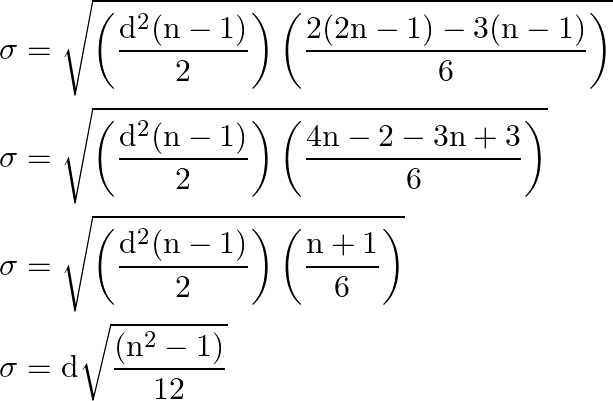
As a result the mean and standard deviation of the given AP is
\mathrm{a}+\frac{(\mathrm{n}-1)}{2} \mathrm{~d} \text { and } \mathrm{d} \sqrt{\frac{\left(\mathrm{n}^{2}-1\right)}{12}} \text { respectively. }

i

More Material