Login/Sign Up
Home » Determine the maximum value of     if the feasible region (shaded) for a LPP is shown in Fig.     .
Determine the maximum value of

    \[\mathbf{Z}\text{ }=\text{ }\mathbf{3}x~+\text{ }\mathbf{4}y~\]

if the feasible region (shaded) for a LPP is shown in Fig.

    \[12.7\]

.
CBSE | Class 12 | Exercise 1 | Linear Programming | Maths | NCERT Exemplar
Determine the maximum value of

    \[\mathbf{Z}\text{ }=\text{ }\mathbf{3}x~+\text{ }\mathbf{4}y~\]

if the feasible region (shaded) for a LPP is shown in Fig.

    \[12.7\]

.

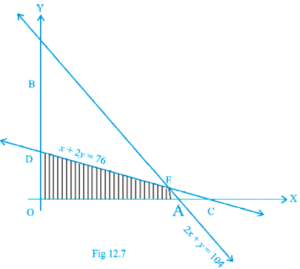
As shown in the figure, OAED is the feasible region.

At A,

    \[y\text{ }=\text{ }0\]

in equation

    \[2x\text{ }+\text{ }y\text{ }=\text{ }104\]

we get,

    \[x=52\]

This is a corner point

    \[A\text{ }=\text{ }\left( 52,\text{ }0 \right)\]

At D,

    \[x=0\]

in equation

    \[x\text{ }+\text{ }2y\text{ }=\text{ }76\]

we get,

    \[y=38\]

This is another corner point

    \[D\text{ }=\text{ }\left( 0,\text{ }38 \right)\]

Now, solving the given equations

    \[x\text{ }+\text{ }2y\text{ }=\text{ }76\]

and

    \[2x\text{ }+\text{ }y\text{ }=\text{ }104\]

we have

    \[2x\text{ }+\text{ }4y\text{ }=\text{ }152\]

    \[2x\text{ }+\text{ }y\text{ }=\text{ }104\]

(-)___(-)____(-)____

    \[3y\text{ }=\text{ }48\Rightarrow y\text{ }=\text{ }16\]

Using the value of y in the equation, we get

    \[x\text{ }+\text{ }2\left( 16 \right)\text{ }=\text{ }76\Rightarrow x\text{ }=\text{ }7632\text{ }=\text{ }44\]

So, the corner point

    \[E\text{ }=\text{ }\left( 44,\text{ }16 \right)\]

On evaluating the maximum value of Z, we get

From the above table it’s seen that the maximum value of Z is

    \[196\]

.

Therefore, the maximum value of the function Z is

    \[196\]

at

    \[\left( 44,\text{ }16 \right)\]

.

i

More Material