Login/Sign Up
Home » 4. If     , compute    
4. If

    \[\mathbf{sin}\text{ }\mathbf{A}\text{ }=~\mathbf{9}/\mathbf{41}\]

, compute

    \[\mathbf{cos}\text{ }\mathbf{A}\text{ }\mathbf{and}\text{ }\mathbf{tan}\text{ }\mathbf{A}.\]

CBSE | Class 10 | Maths | RD Sharma | Trigonometric Ratios | Trigonometric Ratios
4. If

    \[\mathbf{sin}\text{ }\mathbf{A}\text{ }=~\mathbf{9}/\mathbf{41}\]

, compute

    \[\mathbf{cos}\text{ }\mathbf{A}\text{ }\mathbf{and}\text{ }\mathbf{tan}\text{ }\mathbf{A}.\]

Solution:

Given that, 

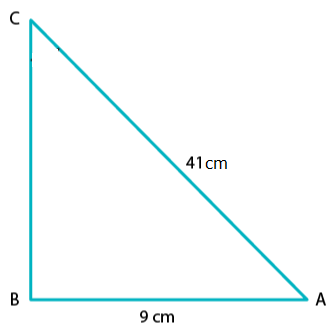
    \[sin\text{ }A\text{ }=\text{ }9/41~\ldots \ldots \ldots \ldots .\text{ }\left( 1 \right)\]

 Required to find:

    \[cos\text{ }A,\text{ }tan\text{ }A\]

By definition, we know that

    \[sin\text{ }A\text{ }=\text{ }Perpendicular/\text{ }Hypotenuse\ldots \ldots \ldots \ldots \ldots \left( 2 \right)\]

On Comparing

    \[eq.\text{ }\left( 1 \right)\text{ }and\text{ }\left( 2 \right),\]

we get;

Perpendicular

    \[side\text{ }=\text{ }9\]

and

    \[Hypotenuse\text{ }=\text{ }41\]

Let’s construct

    \[\vartriangle ABC~\]

as shown below,

And, here the length of base AB is unknown.

Thus, by using Pythagoras theorem in

    \[\vartriangle ABC\]

, we get;

    \[A{{C}^{2}}~=\text{ }A{{B}^{2}}~+\text{ }B{{C}^{2}}\]

    \[{{41}^{2}}~=\text{ }A{{B}^{2}}~+\text{ }{{9}^{2}}\]

    \[A{{B}^{2}}~=\text{ }{{41}^{2}}~\text{ }{{9}^{2}}\]

    \[A{{B}^{2}}~=\text{ }168\text{ }\text{ }81\]

    \[AB=\text{ }1600\]

    \[AB\text{ }=~\surd 1600\]

    \[AB\text{ }=\text{ }40\]

    \[\Rightarrow Base\text{ }of\text{ }triangle\text{ }ABC,\text{ }AB\text{ }=\text{ }40\]

We know that,

    \[cos\text{ }A\text{ }=\text{ }Base/\text{ }Hypotenuse\]

    \[cos\text{ }A\text{ }=AB/AC\]

    \[cos\text{ }A\text{ }=40/41\]

And,

    \[tan\text{ }A\text{ }=\text{ }Perpendicular/\text{ }Base\]

    \[tan\text{ }A\text{ }=\text{ }BC/AB\]

    \[tan\text{ }A\text{ }=\text{ }9/40\]

i

More Material