Login/Sign Up
Home » Find the equation of the plane passing through the line of intersection of the planes and and parallel to -axis.
Find the equation of the plane passing through the line of intersection of the planes \vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=1 and \vec{r} \cdot(2 \hat{i}+3 \hat{j}-\hat{k})+4=0 and parallel to x-axis.
CBSE | Class 12 | Maths | Miscellaneous Exercise | NCERT | Three Dimensional Geometry
Find the equation of the plane passing through the line of intersection of the planes \vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=1 and \vec{r} \cdot(2 \hat{i}+3 \hat{j}-\hat{k})+4=0 and parallel to x-axis.

Solution:

It is known to us that,
The eq. of any plane through the line of intersection of the planes \vec{r} \cdot \overrightarrow{n_{1}}=d_{1} and \vec{r} \cdot \overrightarrow{n_{2}}=d_{2} is given by \left(\vec{r} \cdot \overrightarrow{n_{1}}-d_{1}\right)+\lambda\left(\vec{r} \cdot \overrightarrow{n_{2}}-d_{2}\right)=0
Therefore, the eq. of any plane through the line of intersection of the given planes is
\begin{array}{l} {[\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})-1]+\lambda[\vec{r} \cdot(-2 \hat{i}-3 \hat{j}+\hat{k})-4]=0} \\ \vec{r} \cdot((1-2 \lambda) \hat{i}+(1-3 \lambda) \hat{j}+(1+\lambda) \hat{k})-1-4 \lambda=0 \\ \vec{r} \cdot((1-2 \lambda) \hat{i}+(1-3 \lambda) \hat{j}+(1+\lambda) \hat{k})=1+4 \lambda & \ldots \end{array}
As this plane is parallel to \mathrm{x}-axis.
Therefore, the normal vector of the plane (1) will be perpendicular to x-axis.
Direction ratios of Normal \left(a_{1}, b_{1,} c_{1}\right) \equiv[(1-2 \lambda),(1-3 \lambda),(1+)]
Direction ratios of x-axis \left(a_{2}, b_{2}, c_{2}\right) \equiv(1,0,0),
As the two lines are perpendicular,

\begin{array}{l} a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}=0 \\ (1-2 \lambda) \times 1+(1-3 \lambda) \times 0+(1+\lambda) \times 0=0 \\ (1-2 \lambda)=0 \end{array}
\lambda=1 / 2
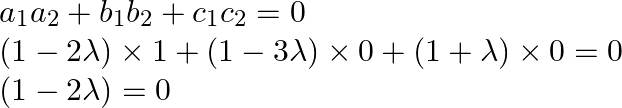
On substituting the value of \lambda in eq.(1), we obtain

\begin{array}{l} \vec{r} \cdot((1-2 \lambda) \hat{i}+(1-3 \lambda) \hat{j}+(1+\lambda) \hat{k})=1+4 \lambda \\ \vec{r} \cdot\left(\left(1-2\left(\frac{1}{2}\right)\right) \hat{i}+\left(1-3\left(\frac{1}{2}\right)\right) \hat{j}+\left(1+\frac{1}{2}\right) \hat{k}\right)=1+4\left(\frac{1}{2}\right) \\ \vec{r} \cdot(0 \hat{i}-\hat{j}+3 \hat{k})=6 \end{array}
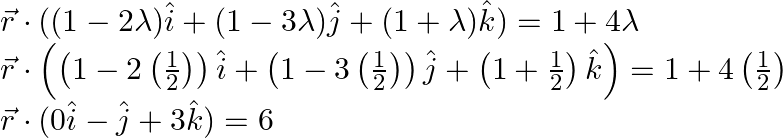
As a result, the eq. of the required plane is \overrightarrow{1} \cdot(0 \hat{i}-\hat{j}+3 \hat{k})=6

i

More Material