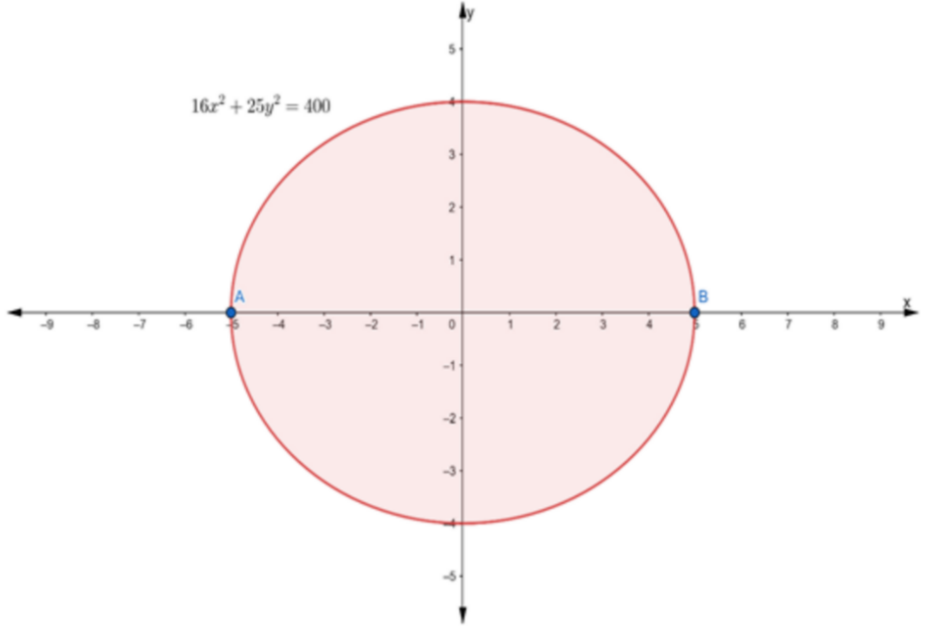
Given:
![\[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aed3022a6a6b09b7823a798e1b61f3a4_l3.png "Rendered by QuickLaTeX.com")
Divide by
![\[400\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f2f3849d6e11b94c00641998e320efbf_l3.png "Rendered by QuickLaTeX.com")
to both the sides, we get
![\[\frac{16}{400}{{x}^{2}}+\frac{25}{400}{{y}^{2}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f1236104de4a1a743f4dcbed20c8c352_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{4}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7fd9524c7bde31c404c464c9a41aba14_l3.png "Rendered by QuickLaTeX.com")
…(i)
Since,
![\[25>4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c5291879c59e8e558efec612d0585a5_l3.png "Rendered by QuickLaTeX.com")
So, above equation is of the form,
![\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d32e615a6517b76e65b04fd25ae8bf0a_l3.png "Rendered by QuickLaTeX.com")
…(ii)
Comparing eq. (i) and (ii), we get
![\[\begin{array}{*{35}{l}} {{a}^{2}}=\text{ }25\text{ }and\text{ }{{b}^{2}}=\text{ }4 \\ \Rightarrow a\text{ }=\text{ }\surd 25\text{ }and\text{ }b\text{ }=\text{ }\surd 4 \\ \Rightarrow a\text{ }=\text{ }5\text{ }and\text{ }b\text{ }=\text{ }2 \\ \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1680cc1ad2d0b3c6930778feb7f9031a_l3.png "Rendered by QuickLaTeX.com")
(i) To find: Length of major axes
Clearly, a > b, therefore the major axes of the ellipse is along x axes.
∴Length of major axes =
![\[2a\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f958c24c5751b6dd1e3af99fcea3885_l3.png "Rendered by QuickLaTeX.com")
![\[=\text{ }2\text{ }\times \text{ }5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a6c11e9f317e90dc7c5f1977ad26a940_l3.png "Rendered by QuickLaTeX.com")
=
![\[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png "Rendered by QuickLaTeX.com")
units
(ii) To find: Coordinates of the Vertices
Clearly, a > b
∴ Coordinate of vertices =
![\[\left( a,\text{ }0 \right)\text{ }and\text{ }\left( -a,\text{ }0 \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bbd758d7b7a619c2b4370aa32f333e30_l3.png "Rendered by QuickLaTeX.com")
![\[=\text{ }\left( 5,\text{ }0 \right)\text{ }and\text{ }\left( -5,\text{ }0 \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d5424f10fe41494232e13fcb06942319_l3.png "Rendered by QuickLaTeX.com")