Find the image of the point (2, -1, 5) in the line
Find the image of the point 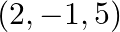 in the line
in the line
Answer
Given: Point 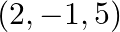
Equation of line 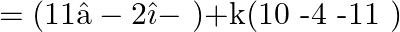
The equation of line can be re-arranged as 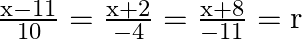
The general point on this line is
Let 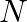 be the foot of the perpendicular drawn from the point
be the foot of the perpendicular drawn from the point 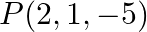 on the given line. Then, this point is
on the given line. Then, this point is 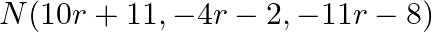 for some fixed value of
for some fixed value of 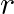 .
.
D.r.’s of PN are 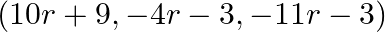
D.r.’s of the given line is 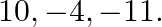
Since, PN is perpendicular to the given line, we have,
Then, the image of the point is
Therefore, the image is 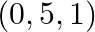 .
.
![]() in the line
in the line![]()
![]()
![]()
![]() be the foot of the perpendicular drawn from the point
be the foot of the perpendicular drawn from the point ![]() on the given line. Then, this point is
on the given line. Then, this point is ![]() for some fixed value of
for some fixed value of ![]() .
.![]()
![]()
![]() .
.