Find the multiplicative inverse of the following complex numbers: (i) 1

Home » Find the multiplicative inverse of the following complex numbers: (i) 1 – i (ii) (1 + i √3)2

Find the multiplicative inverse of the following complex numbers:
(i) 1 – i
(ii) (1 + i √3)2

Find the multiplicative inverse of the following complex numbers:
(i) 1 – i
(ii) (1 + i √3)2

Solution:

(i) $1-\mathrm{i}$
Given that
It is known that the multiplicative inverse of a complex number $(\mathrm{Z})$ is $\mathrm{Z}^{-1}$ or $1 / \mathrm{Z}$ Therefore,
$\begin{array}{l} Z=1-\mathrm{i} \\ Z^{-1}=\frac{1}{1-i} \end{array}$
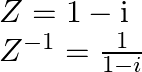
On multiplying and dividing by $(1+\mathrm{i})$ we obtain,
$\begin{array}{l} =\frac{1}{1-i} \times \frac{1+i}{1+i} \\ =\frac{1+i}{1^{2}-(i)^{2}} \\ =\frac{1+i}{1-(-1)}\left[\text { Since, } \mathrm{i}^{2}=-1\right] \\ =\frac{1+i}{2} \end{array}$
As a result, the multiplicative inverse of $(1-i)$ is $(1+i) / 2$

(ii) $(1+i \sqrt{3})^{2}$
Given that
$\begin{array}{l} (1+i \sqrt{3})^{2} \\ Z=(1+i \sqrt{3})^{2} \\ =1^{2}+(i \sqrt{3})^{2}+2(1)(i \sqrt{3}) \\ =1+3 i^{2}+2 i \sqrt{3} \\ =1+3(-1)+2 i \sqrt{3}\left[\text { since, } i^{2}=-1\right] \\ =1-3+2 i \sqrt{3} \\ =-2+2 i \sqrt{3} \end{array}$
It is known that the multiplicative inverse of a complex number $(\mathrm{Z})$ is $\mathrm{Z}^{-1}$ or $1 / \mathrm{Z}$
Therefore,
$\begin{aligned} Z=-2+2 i \sqrt{3} \\ \quad Z^{-1}=\frac{1}{-2+2 i \sqrt{3}} \end{aligned}$
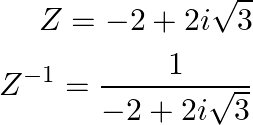
On multiplying and dividing by $-2-2 \mathrm{i} \sqrt{3}$ , we obtain
$\begin{array}{l} =\frac{1}{-2+2 \sqrt{3} i} \times \frac{-2-2 \sqrt{3} i}{-2-2 \sqrt{3} i} \\ =\frac{-2-2 \sqrt{3} i}{(-2)^{2}-(2 \sqrt{3} i)^{2}} \\ =\frac{-2-2 \sqrt{3} i}{4-12 i^{2}} \\ =\frac{-2-2 \sqrt{3} i}{4-12(-1)} \\ =\frac{-2-2 \sqrt{3} i}{16} \\ =\frac{-1}{8} \frac{-i \sqrt{3}}{8} \end{array}$
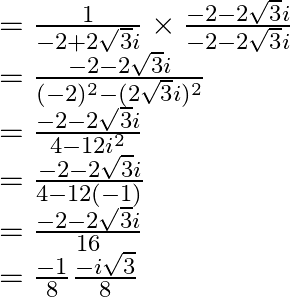
As a result, the multiplicative inverse of $(1+i \sqrt{3})^{2}$ is $(-1-i \sqrt{3}) / 8$