Login/Sign Up
Home » Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
CBSE | Maths | NCERT | Probability
Find the probability of throwing at most 2 sixes in 6 throws of a single die.

Solution:

Let’s say X represents the amount of times you’ve gotten sixes in six die throws. Bernoulli trials are also the repeated tossing of die selection.

As a result, the chances of getting six in a single dice toss are slim. p=1 / 6

Clearly, we have \mathrm{X} has the binomial distribution where \mathrm{n}=6 and \mathrm{p}=1 / 6

And, q=1-p=1-1 / 6=5 / 6

    \[\therefore P(X=x)={ }^{n} C_{x} q^{n-x} p^{x}\]

={ }^{6} C_{x}\left(\frac{5}{6}\right)^{6^{-x}}\left(\frac{1}{6}\right)^{x}

Hence, probability of throwing at most 2 sixes =\mathrm{P}(\mathrm{X} \leq 2)

=P(X=0)+p(X=1)+P(X=2)

={ }^{6} C_{0} \cdot\left(\frac{5}{6}\right)^{6}+{ }^{6} C_{1} \cdot\left(\frac{5}{6}\right) 65 \cdot\left(\frac{1}{6}\right)+{ }^{6} C_{2}\left(\frac{5^{4}}{6}\right) \cdot\left(\frac{1}{6}\right)^{2}

=1 \cdot\left(\frac{5}{6}\right)^{6}+6 \cdot \frac{1}{6} \cdot\left(\frac{5}{6}\right)^{5}+15 \cdot \frac{1}{36} \cdot\left(\frac{5}{6}\right)^{4}

=\left(\frac{5}{6}\right)^{6}+\left(\frac{5}{6}\right)^{5}+\frac{5}{12} \cdot\left(\frac{5}{6}\right)^{4}

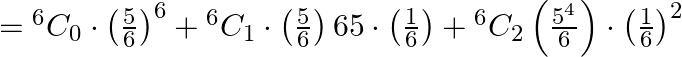
=\left(\frac{5}{6}\right)^{4}\left[\left(\frac{5}{6}\right)^{2}+\left(\frac{5}{6}\right)+\left(\frac{5}{12}\right)\right]

=\left(\frac{5}{6}\right)^{4} \cdot\left[\frac{25+30+15}{36}\right]

=\frac{70}{36} \cdot\left(\frac{5}{6}\right)^{4}

=\frac{35}{18} \cdot\left(\frac{5}{6}\right)^{4}

i

More Material