Solution:
It is known to us that shortest distance between two lines
![]() and
and ![]() is given as:
is given as:
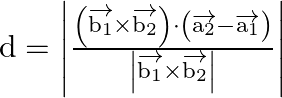
On comparing the equations we obtain,
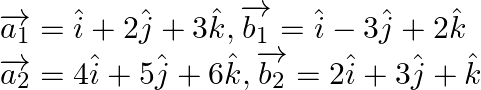
Subtracting the above equations we obtain,
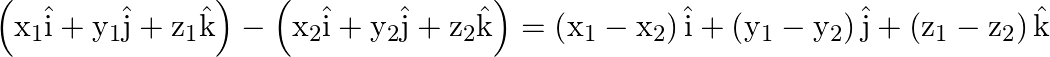
![]() And,
And,
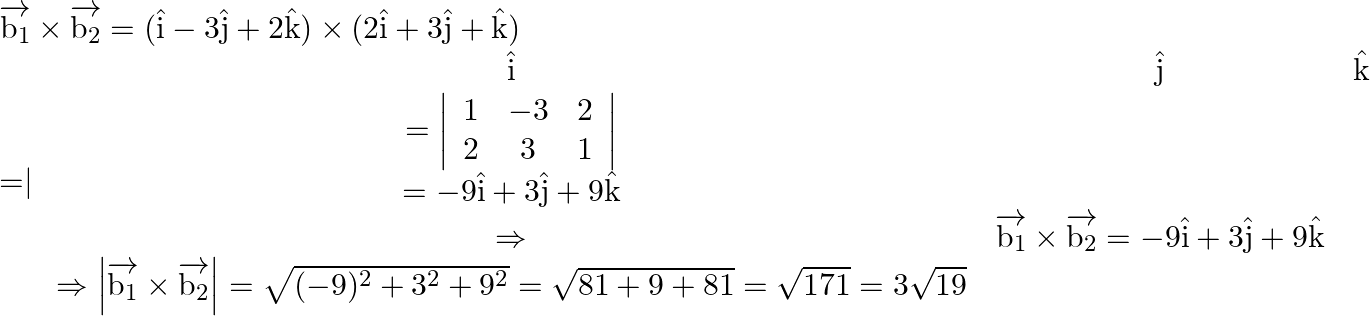
Multiplying eq. (2) and eq. (3) we get,
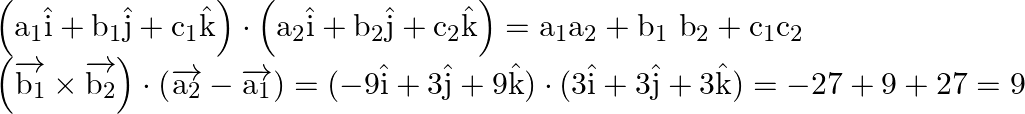
On substituting all the values in eq. (1), we get
The shortest distance between the two lines,
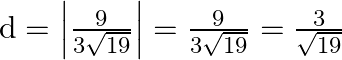
As a result, the shortest distance is ![]()
