Solution:
It is given: set of first ![]() natural numbers
natural numbers
We now need to find the standard deviation
Provided first ![]() natural numbers, it can be written in table as shown below
natural numbers, it can be written in table as shown below
![Rendered by QuickLaTeX.com \[\begin{tabular}{|l|l|l|l|l|l|l|l|l|} \hline $\mathrm{x}_{\mathrm{i}}$ & 1 & 2 & 3 & 4 & 5 & $\ldots$ & $\ldots .$ & $\mathrm{n}$ \\ \hline $\mathrm{x}_{\mathrm{i}}^{2}$ & 1 & 4 & 9 & 16 & 25 & $\ldots .$ & $\ldots .$ & $\mathrm{n}^{2}$ \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5b3cbaddeaa4226cbe0c3740ec41efa9_l3.png)
Therefore, sums of these are
![]()
And
![]()
So, we can write the standard deviation as,
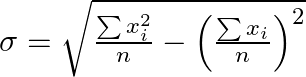
Substitute the values
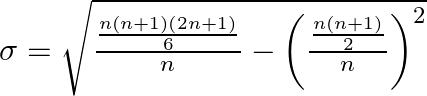
Simplify
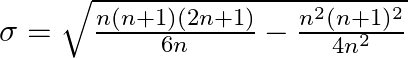
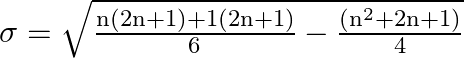
Multiplyi the numerator
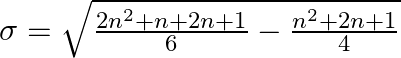
Take LCM and simplify
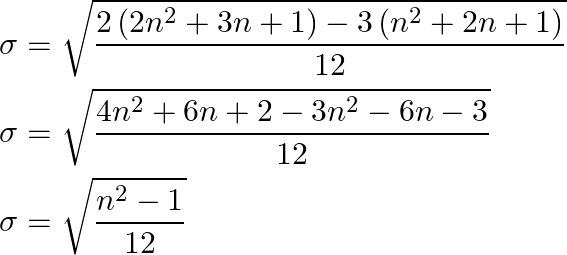
As a result, 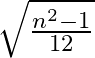 is the standard deviation of the first
is the standard deviation of the first ![]() natural numbers.
natural numbers.
