Solution:
(a) That passes through the point ![]() and the normal to the plane is
and the normal to the plane is ![]()
Let’s say that the position vector of the point ![]() be
be
![]()
It is known that Normal ![]() to the plane is given as:
to the plane is given as:
![]()
Vector eq. of the plane is given as:
![]()
Now,
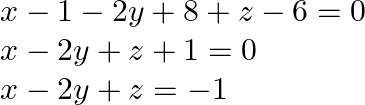
![]() The required Cartesian equation of the plane is
The required Cartesian equation of the plane is ![]()
![]()
Since,
![]()
So eq.(1) becomes,
![Rendered by QuickLaTeX.com \begin{array}{l} (\mathrm{x} \hat{\mathrm{i}}+\mathrm{yj}+z \hat{\mathrm{k}}-\hat{\mathrm{i}}+2 \hat{\mathrm{k}}) \cdot \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}=0 \\ {[(\mathrm{x}-1) \hat{\mathrm{i}}+\mathrm{yj}+(z+2) \hat{\mathrm{k}}] \cdot \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}=0} \\ \mathrm{x}-1+\mathrm{y}-\mathrm{z}-2=0 \\ \mathrm{x}+\mathrm{y}-\mathrm{z}-3=0 \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-79ace66d85a46c40646062ee351e0e6a_l3.png)
As a result, the required Cartesian equation of the plane is ![]()
(b) That passes through the point ![]() and the normal vector to the plane is
and the normal vector to the plane is ![]()
Let’s say that the position vector of the point ![]() be
be
![]()
It is known that Normal ![]() to the plane is given as:
to the plane is given as:
![]()
Vector eq. of the plane is given as:
![]()
Now,
![]()
Since,
![]()
So eq.(1) becomes,
![]()
![Rendered by QuickLaTeX.com \begin{array}{l} \quad[(x-1) \hat{i}+(y-4) \hat{j}+(z-6) \hat{k}] \hat{i}-2 \hat{j}+\hat{k}=0 \\ x-1-2 y+8+z-6=0 \\ x-2 y+z+1=0 \\ x-2 y+z=-1 \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c9a99549cf504a6dba1b54b372fd7eb1_l3.png)
As a result, the required Cartesian equation of the plane is ![]()
