Find the vector equation of a line passing through the point having the position vector and parallel to the line joining the points with position vectors and
Also, find the Cartesian equivalents of this equation.
Answer
line passes through the point with position vector and parallel to the line joining the points with position vectors and .
Io find: equation of line in vector and Cartesian forms
Formula Used: Equation of a line is
Vector form:
Cartesian form: .
where is a point on the line and with being the direction ratios of the line.
Explanation:
Here,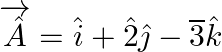
The direction ratios of the line are

$\begin{array}{l}\Rightarrow –1:–4:9\\ \Rightarrow 1:4:–9\\ \text{ So, }\overrightarrow{\mathrm{b}}=\hat{\mathrm{l}}+4\hat{ȷ}–9\overrightarrow{\mathrm{k}}\end{array}$
\begin{array}{l}
\Rightarrow-1:-4: 9 \\
\Rightarrow 1: 4:-9 \\
\text { So, } \overrightarrow{\mathrm{b}}=\hat{\mathrm{l}}+4 \hat{\jmath}-9 \overrightarrow{\mathrm{k}}
\end{array}

Therefore,
Vector form:

$\overrightarrow{r}=\hat{i}+2\hat{ı}–3\hat{k}–+–\lambda (\hat{i}+4–4\hat{ı}–9\hat{k})$
\vec{r}=\hat{i}+2 \hat{\imath}-3 \hat{k}-+-\lambda(\hat{i}+4-4 \hat{\imath}-9 \hat{k})

Cartesian form:

$\frac{x–1}{1}=\frac{y–2}{1}=\frac{z+3}{–9}$
\frac{x-1}{1}=\frac{y-2}{1}=\frac{z+3}{-9}