Login/Sign Up
Home » Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane
Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane \vec{r} \cdot(\hat{i}+2 \hat{j}-5 \hat{k})+9=0
CBSE | Class 12 | Maths | Miscellaneous Exercise | NCERT | Three Dimensional Geometry
Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane \vec{r} \cdot(\hat{i}+2 \hat{j}-5 \hat{k})+9=0

Solution:

The vector eq. of a line passing through a point with position vector \vec{a} and parallel to vector \vec{b} is given as
\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}
Given that the line passes through (1,2,3)
Therefore, \vec{a}=1 \hat{i}+2 \hat{j}+3 \hat{k}
Let’s find the normal of plane
\begin{array}{l} \overrightarrow{\mathrm{r}} \cdot(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-5 \hat{\mathrm{k}})+9=0 \\ \overrightarrow{\mathrm{r}} \cdot(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-5 \hat{\mathrm{k}})=-9 \\ -\overrightarrow{\mathrm{r}} \cdot(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-5 \hat{\mathrm{k}})=9 \\ \overrightarrow{\mathrm{r}} \cdot(-1 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+5 \hat{\mathrm{k}})+9=0 \end{array}
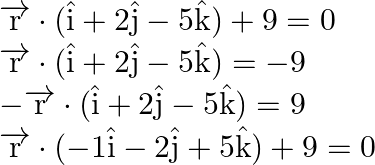
Now compare it with \overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{n}}=\mathrm{d}
\overrightarrow{\mathrm{n}}=-\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}
As line is perpendicular to plane, the line will be parallel of the plane
\therefore \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{n}}=-\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}
Therefore,
\begin{array}{l} \overrightarrow{\mathrm{r}}=(1 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})+\lambda(-\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}) \\ \overrightarrow{\boldsymbol{r}}=(1 \hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}+3 \hat{\boldsymbol{k}})-\lambda(\hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}-5 \hat{\boldsymbol{k}}) \end{array}
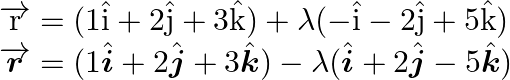
As a resullt, the required vector equation of line is \vec{r}=(1 \hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}+3 \hat{\boldsymbol{k}})-\lambda(\hat{\boldsymbol{i}}+2 \hat{\boldsymbol{j}}-5 \hat{\boldsymbol{k}})

i

More Material