Equation of the family of an ellipse having foci on the ![]() -axis and centers at the origin can be represented by
-axis and centers at the origin can be represented by ![]()
![]()
Differentiating the above equation with respect to ![]() on both sides, we have,
on both sides, we have,
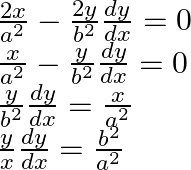
Again differentiating the above equation with respect to ![]() on both sides, we have,
on both sides, we have,
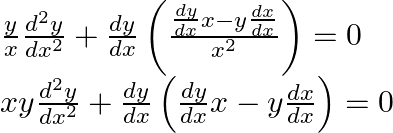
Rearranging the above equation
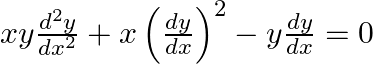
This is the required differential equation.
Form the differential equation of the family of hyperbolas having foci on the 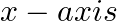 and centers at the origin.
and centers at the origin.
Form the differential equation of the family of hyperbolas having foci on the 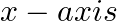 and centers at the origin.
and centers at the origin.
