Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.

Home » Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.

Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.

Equation of the family of circles in the second quadrant and touching the coordinate axes
can be represented by

$(x-(-a))^{2}+(y-a)^{2}=a^{2}$ , where $a$ is an arbitrary constants.
$(x+a)^{2}+(y-a)^{2}=a^{2}(1)$
Differentiating the above equation with respect to $x$ on both sides, we have,
$\begin{array}{l} 2(x+a)+2(y-a) \frac{d y}{d x}=0 \\ x+a-a \frac{d y}{d x}+y \frac{d y}{d x}=0 \\ a=\frac{x+y \frac{d y}{d x}}{\frac{d y}{d x}-1} \end{array}$
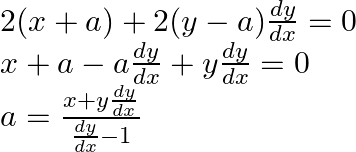
Substituting the value of a in equation (1)
$\begin{array}{l} \left(x+\frac{x+y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2}+\left(y-\frac{x+y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2}=\left(\frac{x+y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2} \\ \left(\frac{x \frac{d y}{d x}-x+x+y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2}+\left(\frac{y \frac{d y}{d x}-y-x-y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2}=\left(\frac{x+y \frac{d y}{d x}}{\frac{d y}{d x}-1}\right)^{2} \\ \left(x \frac{d y}{d x}-x+x+y \frac{d y}{d x}\right)^{2}+\left(y \frac{d y}{d x}-y-x-y \frac{d y}{d x}\right)^{2}=\left(x+y \frac{d y}{d x}\right)^{2} \\ \left(\frac{d y}{d x}\right)^{2}(x+y)^{2}+(-y-x)^{2}=\left(x+y \frac{d y}{d x}\right)^{2} \\ \left(\frac{d y}{d x}\right)^{2}(x+y)^{2}+(y+x)^{2}=\left(x+y \frac{d y}{d x}\right)^{2} \end{array}$
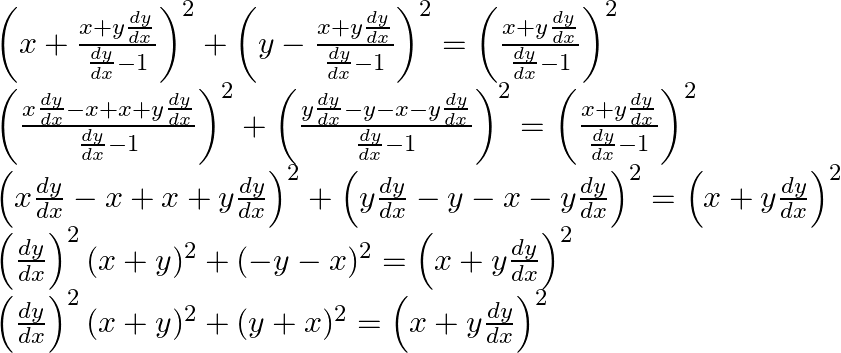
Rearranging the above equation
$(x+y)^{2}\left\{\left(\frac{d y}{d x}\right)^{2}+1\right\}=\left(x+y \frac{d y}{d x}\right)^{2}$
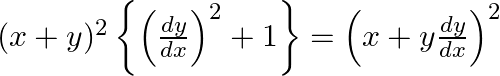
This is the required differential equation.