Solution:
We have 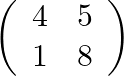 .
.
The transpose of the matrix is an operation of making interchange of elements by the rule on positioned element ![]() shifted to new position
shifted to new position ![]() .
.
The symmetric matrix is defined as similarity of transpose of matrix with it self. i.e, ![]() .
.
The skew-symmetric matrix is defined as similarity of transpose of matrix with it self. i.e, ![]() .
.
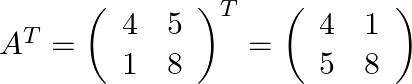
Therefore finally we have
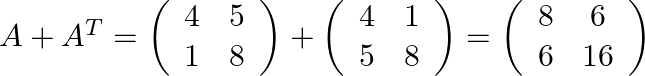
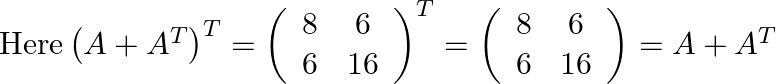
Therefore ![]() is symmetric.
is symmetric.

![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}4 & 5 \\ 1 & 8\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8158b32a662df332e0a5eb4fe7a2edb9_l3.png) , show that
, show that