Solution:
Let’s consider ![]() be the direction cosines of the line perpendicular to each of the given lines.
be the direction cosines of the line perpendicular to each of the given lines.
Therefore, ![]()
And ![]()
On solving eq.(1) and eq.(2) by using cross – multiplication, we obtain
![]()
Therefore, the direction cosines of the given line are proportional to
![]()
![]()
Therefore, its direction cosines are
![]()
Where,
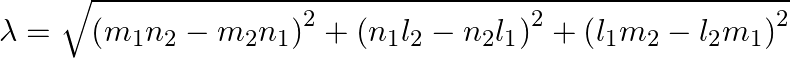
Where,
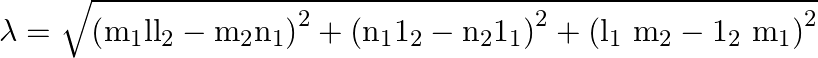
It is known to us that
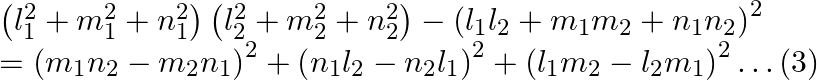
Given that the given lines are perpendicular to each other.
Therefore, ![]()
Also, we have
![]()
And, ![]()
On substituting these values in eq. (3), we have
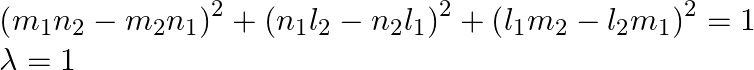
As a result, the direction cosines of the given line are ![]()
