If the plane 2x – 3y – 6z = 13 makes an angle
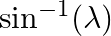
with the x-axis, then find the value of λ.
Answer:
Direction ratios of the x-axis are 1,0,0 and direction ratios of normal to the plane are 2,−3,−6.
The angle between the line and the plane,
Let 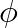 be the angle between the
be the angle between the  -axis and the given plane.
-axis and the given plane.
Hence, 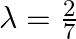 .
.
![]() be the angle between the
be the angle between the ![]() -axis and the given plane.
-axis and the given plane.![]() .
.![]() be the angle between the
be the angle between the ![]() -axis and the given plane.
-axis and the given plane.![]() .
.