Solution:
It is given that: ![]()
Here, ![]() is the principal,
is the principal, ![]() is the rate of interest per annum and
is the rate of interest per annum and ![]() is the time in years.
is the time in years.
On solving the differential equation we obtain,
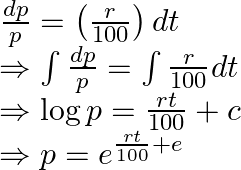
As the principal doubles itself in 10 years, therefore
Suppose the initial interest be ![]() (for
(for ![]() ), after 10 years
), after 10 years ![]() becomes
becomes ![]() .
.
As a result, ![]() for
for ![]() (i)
(i)
![]()
Substituting equation(i) in equation(ii), we obtain,
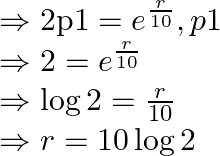
![]()
![]() Rate of interest
Rate of interest ![]()
