Solution:
Suppose ![]() be a relation defined on A. (As given)
be a relation defined on A. (As given)
If ![]() is Reflexive, Symmetric and Transitive, therefore
is Reflexive, Symmetric and Transitive, therefore ![]() is an equivalence relation.
is an equivalence relation.
So now,
Reflexivity:
Suppose ![]() be an arbitrary element of
be an arbitrary element of ![]()
we have,
![]() since, every triangle is similar to itself.
since, every triangle is similar to itself.
![]() and
and ![]()
Therefore, ![]() is reflexive.
is reflexive.
Symmetric:
Suppose ![]() and
and ![]() , such that
, such that ![]()
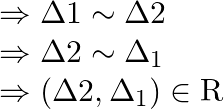
Therefore, ![]() is symmetric
is symmetric
Transitivity:
Suppose ![]() such that
such that ![]() and
and ![]()
![]() and
and ![]()
![]()
![]()
Therefore, ![]() is transitive.
is transitive.
As a result, ![]() is an equivalence relation.
is an equivalence relation.
