Solution:
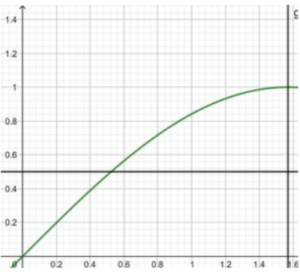
![]() for given function
for given function ![]()
Recalling the graph for ![]() , we realise that for any two values on the curve, say
, we realise that for any two values on the curve, say ![]() and
and ![]() ,
,
![]()
As a result, ![]() is one to one.
is one to one.
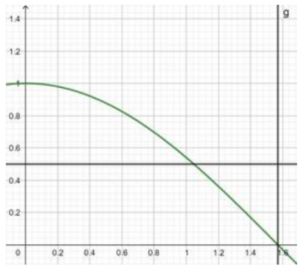
![]() for given function
for given function ![]()
![]()
Recalling the graph for ![]() , we realise that for any two values on the curve, say
, we realise that for any two values on the curve, say ![]() and
and ![]() ,
, ![]()
As a result, ![]() is one to one.
is one to one.
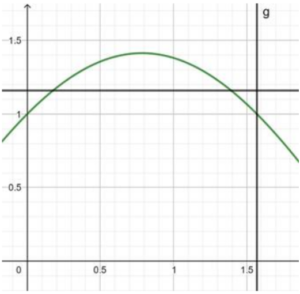
Now, ![]() mapped from
mapped from ![]() to
to ![]()
Recalling the graph for ![]() , we realise that for any two values on the curve, say
, we realise that for any two values on the curve, say ![]() and
and ![]() ,
,
![]()
As a result, ![]() is not one to one.
is not one to one.
i.e. ![]() is not one to one, even though
is not one to one, even though ![]() ar individually.
ar individually.
