Answer is (B)
M.I of rod whose axis of rotation is passing through center and perpendicular to the plane of rod is ![]() and
and ![]() (where K.J radius of gravitation)
(where K.J radius of gravitation)
![]()
When axis of rotation of rod is passing through one and of rod, then
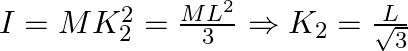
Taking ratios of ![]() and
and ![]() we get
we get
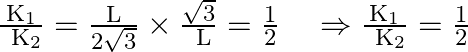
Let ‘ 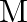 ‘ be the mass and ‘
‘ be the mass and ‘ 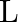 ‘ be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
‘ be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
A) 1
B)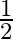
C)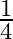
D)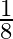
A) 1
B)
C)
D)
Let ‘ 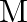 ‘ be the mass and ‘
‘ be the mass and ‘ 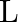 ‘ be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
‘ be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
A) 1
B)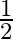
C)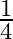
D)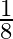
A) 1
B)
C)
D)
