Maximize $\mathrm{Z}=\mathbf{x}+\mathbf{y}$ subject to $\mathbf{x}+4 \mathbf{y} \leq \mathbf{8}, 2 \mathbf{x}+3 \mathbf{y} \leq \mathbf{1 2}, 3 \mathbf{x}+\mathbf{y} \leq \mathbf{9}, \mathbf{x} \geq \mathbf{0}, \mathbf{y} \geq \mathbf{0}$.

Home » Maximize subject to .

Maximize $\mathrm{Z}=\mathbf{x}+\mathbf{y}$ subject to $\mathbf{x}+4 \mathbf{y} \leq \mathbf{8}, 2 \mathbf{x}+3 \mathbf{y} \leq \mathbf{1 2}, 3 \mathbf{x}+\mathbf{y} \leq \mathbf{9}, \mathbf{x} \geq \mathbf{0}, \mathbf{y} \geq \mathbf{0}$ .

CBSE | Class 12 | Linear Programming | Maths | NCERT Exemplar

Maximize $\mathrm{Z}=\mathbf{x}+\mathbf{y}$ subject to $\mathbf{x}+4 \mathbf{y} \leq \mathbf{8}, 2 \mathbf{x}+3 \mathbf{y} \leq \mathbf{1 2}, 3 \mathbf{x}+\mathbf{y} \leq \mathbf{9}, \mathbf{x} \geq \mathbf{0}, \mathbf{y} \geq \mathbf{0}$ .

Solution:

It is given that: $Z=x+y$ subject to constraints, $x+4 y \leq 8$

$2 x+3 y \leq 12,3 x+y \leq 9, x \geq 0, y \geq 0$

Now construct a constrain table for the above, we have

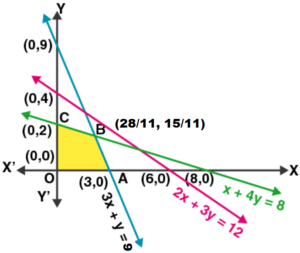
Here, it can be seen that $\mathrm{OABC}$ is the feasible region

Table for $x+4 y=8$

$\begin{tabular}{|l|l|l|} \hline $\mathrm{x}$ & 0 & 8 \\ \hline $\mathrm{y}$ & 2 & 0 \\ \hline \end{tabular}$

Table for $2 x+3 y=12$

$\begin{tabular}{|l|l|l|} \hline $\mathrm{x}$ & 0 & 6 \\ \hline $\mathrm{y}$ & 4 & 0 \\ \hline \end{tabular}$

Table for $3 x+y=9$

$\begin{tabular}{|l|l|l|} \hline $\mathrm{x}$ & 3 & 0 \\ \hline $\mathrm{y}$ & 0 & 9 \\ \hline \end{tabular}$

On solving equations $x+4 y £ 8$ and $3 x+y £ 9$ , we obtain
$x=28 / 11 \text { and } y=15 / 11$
Here, it can be seen that $\mathrm{OABC}$ is the feasible region whose corner points are $\mathrm{O}(0,0), \mathrm{A}(3,0), \mathrm{B}(28 / 11,15 / 11)$ and $\mathrm{C}(0,2) .$

Let’s evaluate the value of $Z$

$\begin{tabular}{|l|l|} \hline Corner points & Value of $Z=x+y$ \\ \hline $0(0,0)$ & $Z=0+0=0$ \\ \hline$A(3,0)$ & $Z=3+0=3$ \\ \hline$B(28 / 11,15 / 11)$ & $Z=28 / 11+15 / 11=43 / 11=3.9$ \\ \hline \end{tabular}$