Login/Sign Up
Home » Maximize the function     , subject to the constraints:     .
Maximize the function

    \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]

, subject to the constraints:

    \[x~\text{£}\text{ }\mathbf{3},~y~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]

.
CBSE | Class 12 | Exercise 1 | Linear Programming | Maths | NCERT Exemplar
Maximize the function

    \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]

, subject to the constraints:

    \[x~\text{£}\text{ }\mathbf{3},~y~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]

.

According to the question:

    \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]

and the constraints 

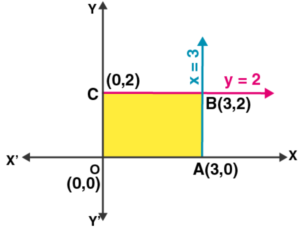
    \[x~\text{£}\text{ }\mathbf{3},~y~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]

.

Plotting all the constrain equations we see that the shaded area OABC is the feasible region determined by the constraints.

The feasible region is bounded with four corner points

    \[O\left( 0,\text{ }0 \right),\text{ }A\left( 3,\text{ }0 \right),\text{ }B\left( 3,\text{ }2 \right)\text{ }and\text{ }C\left( 0,\text{ }2 \right)\]

.

So, the maximum value can occur at any corner.

On evaluating the value of Z, we get

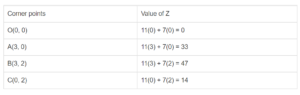
From the above table it’s seen that the maximum value of Z is

    \[47\]

.

Therefore, the maximum value of the function Z is

    \[47\]

at

    \[\left( 3,\text{ }2 \right)\]

.

i

More Material