Linear mass density of the string is given as ![]()
Frequency of the tuning fork is given as ![]()
Mass on the pan is given as ![]()
Tension on the string will be, ![]()
Amplitude is given as ![]()
For a transverse wave, the velocity can be calculated as,
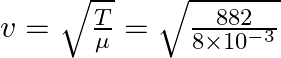
![]()
Angular frequency, ![]()
![]()
Wavelength will be ![]()
Propagation constant will be ![]()
![]()
The general equation of the wave is
![]()
On Substituting all the values we get
![]()
![]() and
and ![]() are in metre and
are in metre and ![]() is in seconds.
is in seconds.
