Prove that the lines and intersect each other and find the point of their intersection.
Answer
Given: The equations of the two lines are and
To Prove: The two lines intersect and to find their point of intersection.
Formula Used: Equation of a line is
Vector form: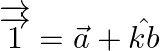
Cartesian form: .
where is a point on the line and is the direction ratios of the line.
Proof:
Let

$\begin{array}{l}\frac{x–4}{1}=\frac{y+3}{1}=\frac{z+1}{7}={\lambda }_1\\ \frac{x–1}{\sqrt{1}}=\frac{y+1}{–3}=\frac{z+10}{8}={\lambda }_2\end{array}$
\begin{array}{l}
\frac{x-4}{1}=\frac{y+3}{1}=\frac{z+1}{7}=\lambda_{1} \\
\frac{x-1}{\sqrt{1}}=\frac{y+1}{-3}=\frac{z+10}{8}=\lambda_{2}
\end{array}

So a point on the first line is
A point on the second line is
If they intersect they should have a common point.

$\begin{array}{l}{\lambda }_1+4=2{\lambda }_2+1\Rightarrow {\lambda }_1–2{\lambda }_2=–3\dots \\ 4{\lambda }_1–3=–3{\lambda }_2–1\Rightarrow 4{\lambda }_1+3{\lambda }_2=2\dots \end{array}$
\begin{array}{l}
\lambda_{1}+4=2 \lambda_{2}+1 \Rightarrow \lambda_{1}-2 \lambda_{2}=-3 \ldots \\
4 \lambda_{1}-3=-3 \lambda_{2}-1 \Rightarrow 4 \lambda_{1}+3 \lambda_{2}=2 \ldots
\end{array}

Solving (1) and (2),

$\begin{array}{l}11{\lambda }_2=14\\ {\lambda }_2=\frac{14}{11}\end{array}$
\begin{array}{l}
11 \lambda_{2}=14 \\
\lambda_{2}=\frac{14}{11}
\end{array}

Therefore,
Substituting for the z coordinate, we get
and
So, the lines do not intersect.