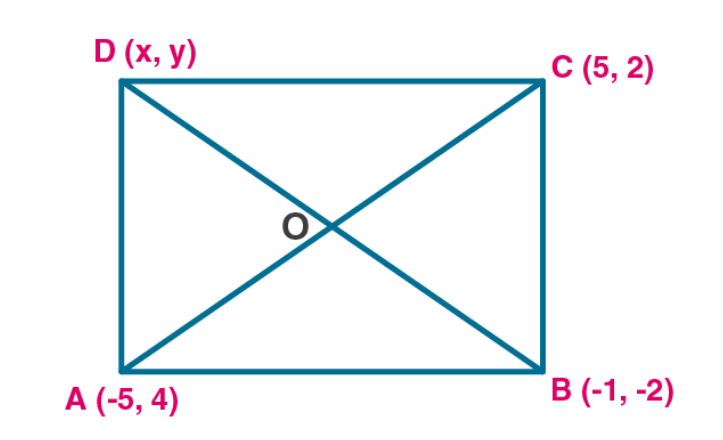
Given points are A(-5,4), B(-1,-2) and C(5,2) are given.
Since these are vertices of an isosceles triangle ABC then AB = BC.
By distance formula, d(AB) = √[(x2-x1)2+(y2-y1)2]
Here x1 = -5, y1 = 4
x2 = -1, y2 = -2
d(AB) = √[(-1-(-5))2+(-2-4)2]
d(AB) = √[(4)2+(6)2]
d(AB) = √(16+36)
d(AB) = √52 …(i)
By distance formula, d(BC) = √[(x2-x1)2+(y2-y1)2]
Here x1 = -1, y1 = -2
x2 = 5, y2 = 2
d(BC) = √[(5-(-1))2+(2-(-2))2]
d(BC) = √[(6)2+(4)2]
d(BC) = √(36+16)
d(BC) = √52 …(ii)
From (i) and (ii) AB = BC
So given points are the vertices of isosceles triangle.
By distance formula, d(AC) = √[(x2-x1)2+(y2-y1)2]
Here x1 = -5, y1 = 4
x2 = 5, y2 = 2
d(AC) = √[(5-(-5))2+(2-4)2]
d(AC) = √[(10)2+(-2)2]
d(AC) = √(100+4)
d(AC) = √104 ….(iii)
Apply Pythagoras theorem to triangle ABC
AB2+BC2 = (√52)2+(√52)2
= 52+52
= 104 ….(iv)
AC2 = (√104)2 = 104…(v)
From (iv) and (v) we got
AB2+BC2 = AC2
So Pythagoras theorem is satisfied.
So the triangle is an isosceles right angled triangle.
Hence proved.
If ABCD is a square, let the diagonals meet at O.
Diagonals of a square bisect each other. So, O is the midpoint of AC and BD.
Consider A-O-C
x1 = -5, y1 = 4
x2 = 5, y2 = 2
By midpoint formula, x = (x1+x2)/2
x = (-5+5)/2 = 0/2 = 0
By midpoint formula, y = (y1+y2)/2
y = (4+2)/2 = 6/2 = 3
So co-ordinate of O is (0,3).
Consider B-O-D
Let co-ordinate of D be (x2,y2)
x1 = -1, y1 = -2
x = 0, y = 3
By midpoint formula, x = (x1+x2)/2
0 = (-1+x2)/2
-1+x2 = 0
x2 = 1
By midpoint formula, y = (x1+x2)/2
3 = (-2+y2)/2
6 = -2+y2
y2 = 6+2 = 8
Hence the co-ordinates of the point D are (1,8).
